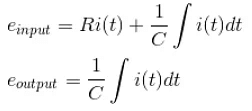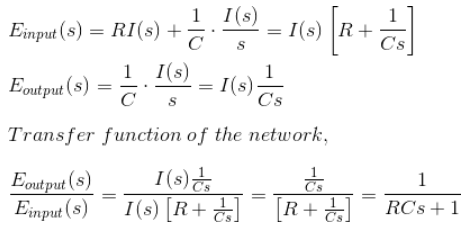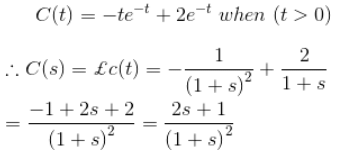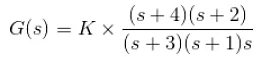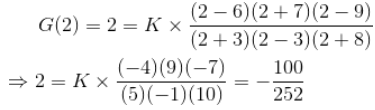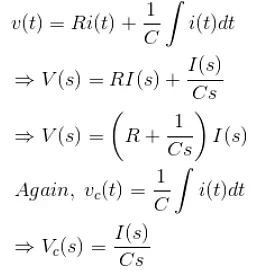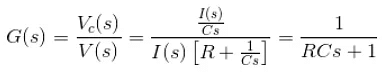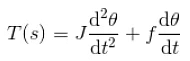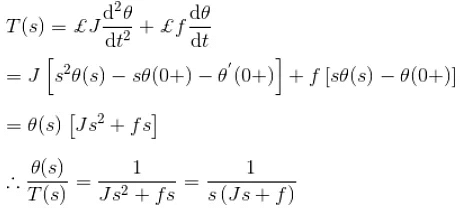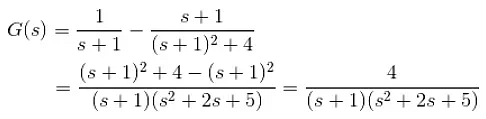Detailed Notes: Transfer Function | Control Systems - Electrical Engineering (EE) PDF Download

Introduction

• A transfer function represents the relationship between the output signal of a control system and the input signal, for all possible input values. A block diagram is a visualization of the control system which uses blocks to represent the transfer function, and arrows which represent the various input and output signals.
• For any control system, there exists a reference input known as excitation or cause which operates through a transfer operation (i.e. the transfer function) to produce an effect resulting in controlled output or response.
• Thus the cause and effect relationship between the output and input is related to each other through a transfer function.
  
• In a Laplace Transform, if the input is represented by R(s) and the output is represented by C(s), then the transfer function will be:
  
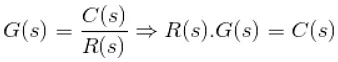
• That is, the transfer function of the system multiplied by the input function gives the output function of the system.

What is a Transfer Function

• The transfer function of a control system is defined as the ratio of the Laplace transform of the output variable to Laplace transform of the input variable assuming all initial conditions to be zero.
  G(s) = C(s)/R(s)
• Procedure for determining the transfer function of a control system are as follows:
  • We form the equations for the system.
  • Now we take Laplace transform of the system equations, assuming initial conditions as zero.
  • Specify system output and input.
  • Lastly we take the ratio of the Laplace transform of the output and the Laplace transform of the input which is the required transfer function.
• It is not necessary that output and input of a control system are of same category. For example, in electric motors the input is electrical signal whereas the output is mechanical signal since electrical energy required to rotate the motors. Similarly in an electric generator, the input is mechanical signal and the output is electrical signal, since mechanical energy is required to produce electricity in a generator.
• But for mathematical analysis, of a system all kinds of signals should be represented in a similar form. This is done by transforming all kinds of signal to their Laplace form. Also the transfer function of a system is represented by Laplace form by dividing output Laplace transfer function to input Laplace transfer function. Hence a basic block diagram of a control system can be represented as
  

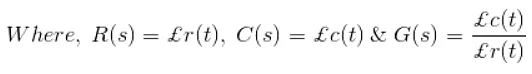
• Where r(t) and c(t) are time domain function of input and output signal respectively.

Methods of Obtaining a Transfer Function

There are major two ways of obtaining a transfer function for the control system. The ways are:

• Block Diagram Method: It is not convenient to derive a complete transfer function for a complex control system. Therefore the transfer function of each element of a control system is represented by a block diagram. Block diagram reduction techniques are applied to obtain the desired transfer function.
• Signal Flow Graphs: The modified form of a block diagram is a signal flow graph. Block diagram gives a pictorial representation of a control system. Signal flow graph further shortens the representation of a control system.

Poles and Zeros of Transfer Function

• Generally, a function can be represented to its polynomial form. For example,
  
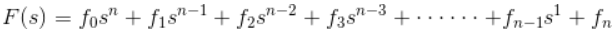
• Now similarly transfer function of a control system can also be represented as
  
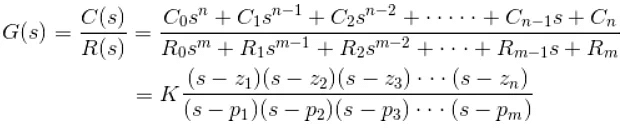
• Where K is known as the gain factor of the transfer function.
• Now in the above function if s = z₁, or s = z₂, or s = z₃,….s = z_n, the value of transfer function becomes zero. These z₁, z₂, z₃,….z_n, are roots of the numerator polynomial. As for these roots the numerator polynomial, the transfer function becomes zero, these roots are called zeros of the transfer function.
• Now, if s = p₁, or s = p₂, or s = p₃,….s = pm, the value of transfer function becomes infinite. Thus the roots of denominator are called the poles of the function.
• Now let us rewrite the transfer function in its polynomial form.
  
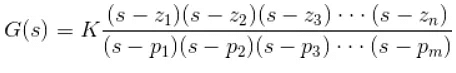
• Now, let us consider s approaches to infinity as the roots are all finite number, they can be ignored compared to the infinite s. Therefore
  
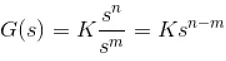
• Hence, when s → ∞ and n > m, the function will have also value of infinity, that means the transfer function has poles at infinite s, and the multiplicity or order of such pole is n – m.
• Again, when s → ∞ and n < m, the transfer function will have value of zero that means the transfer function has zeros at infinite s, and the multiplicity or order of such zeros is m – n.

Concept of Transfer Function

• The transfer function is generally expressed in Laplace Transform and it is nothing but the relation between input and output of a system. Let us consider a system consists of a series connected resistance (R) and inductance (L) across a voltage source (V).
  
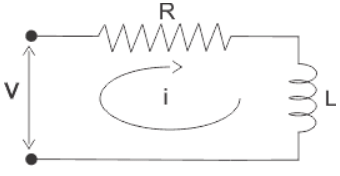
• In this circuit, the current ‘i’ is the response due to applied voltage (V) as cause. Hence the voltage and current of the circuit can be considered as input and output of the system respectively.
• From the circuit, we get,
  
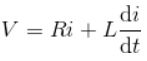
• Now applying Laplace Transform, we get,
  

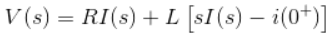
[∵ Initially inductor behaves as open, hence, i(0⁺) = 0]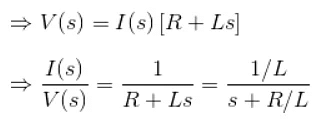

• The transfer function of the system, G(s) = I(s)/V(s), the ratio of output to input.

The Effect of Impulse Signal

• The unit impulse signal is defined as
  
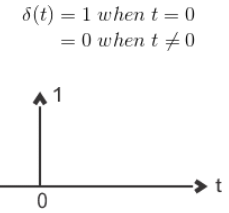
• Laplace transform of unit impulse function is 1.
  
• Now if input signal is unit impulse signal then,
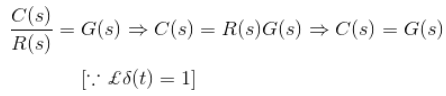
• The output function is same as its transfer function.

Example of Transfer Function

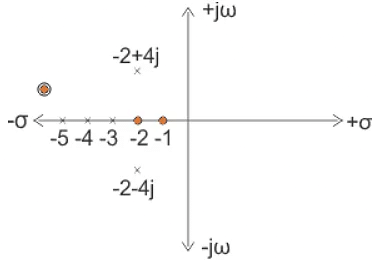
Example 1. Let us explain the concept of poles and zeros of transfer function through an example.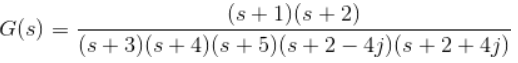

The zeros of the function are, -1, -2 and the poles of the functions are -3, -4, -5, -2 + 4j, -2 – 4j.
Here n = 2 and m = 5, as n < m and m – n = 3, the function will have 3 zeros at s → ∞. The poles and zeros are plotted in the figure below poles and zeros of transfer function

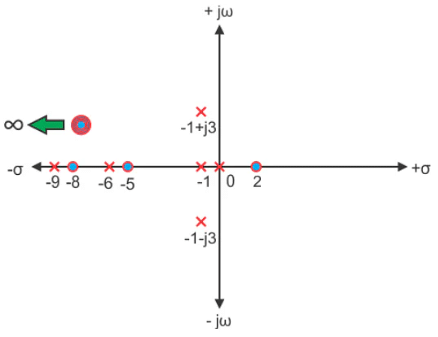
Example 2. Let us take another example of transfer function of control system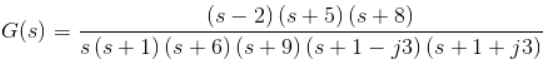

In the above transfer function, if the value of numerator is zero, then

(s — 2) (s + 5) (s + 8) = 0
⇒ s = 2, —5, —8

These are the location of zeros of the function.

Similarly, in the above transfer function, if the value of denominator is zero, then

s (s + 1) (s + 6) (s + 9) (s + 1 — j3) (s + 1 + j3) = 0
⇒ s = 0, —1, —6, —9, —1 + j3, —1 — j3
These are the location of poles of the function.

As the number of zeros should be equal to number of poles, the remaining three zeros are located at s →∞.

Example 3.

In the above network it is obvious that

Let us assume,

Taking the Laplace transform of above equations with considering the initial condition as zero, we get,

Example 4. The impulse response of a system is

C(t) = —te^-t + 2e^-t when (t > 0)
What will be the transfer function of the system?

For impulse response, the output C(s) of the system is equal to transfer function of the system.

Therefore, transfer function of the system is

Example 5. Find the poles and zeros of the function

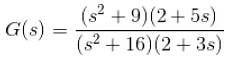
Example 6. The poles and zeros are plotted on the is plain as shown below

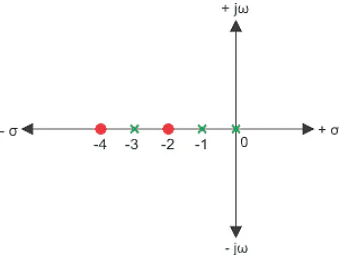
Find the transfer function.

Here, the poles are s = – 3, – 1, 0.

Therefore, denominator of the function would be,
(s + 3)(s + 1)s

the zeros are, -4, – 2.

Therefore, numerator of the function would be,
(s + 4)(s + 2)

Therefore, transfer function would be,

Where, K is the gain factor of the control system.

Example 7. Find the gain factor K of a transfer function whose value is 2 at s = 2 and the transfer function is given as

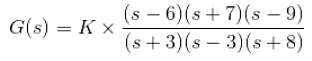
Now, as per condition of the problem,

Example 8. Find the transfer function of the following network.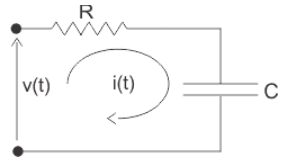

From the circuit we get,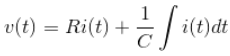

Now applying Laplace transformation at both sides we get,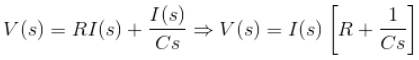

As the applied voltage is cause and the corresponding charging current is the effect, the applied voltage can be considered as input and charging current can be considered as output.

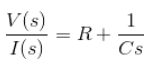
Example 9. Find the transfer function of the network given below,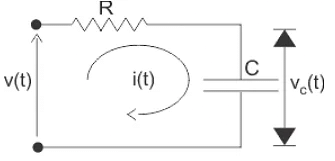

In the above figure, the input is applied voltage v(t) and the output is measured as the voltage appears across the capacitor C that is vc(t).

Laplace transformation of the transfer function is

Example 10. A shaft of innertia J is rotated for an angle θ due to applied torque T against a bearing friction f. Find the transfer function of the system.

The differential equation form of the above statement is

Taking Laplace transformation of both sides of the system,

As the applied torque is input and the output angular displacement is output of the system.

Example 11. The impulse response of the system is given by c(t) = 1 – te^-2t + sin3t. Find that transfer function of the system

Example 12. Find the transfer function of the impulse response of a system given by
g(t) = e^-t(1 - cos 2t)