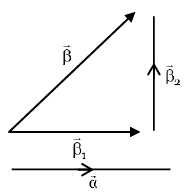
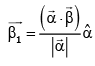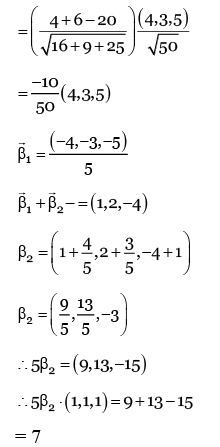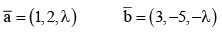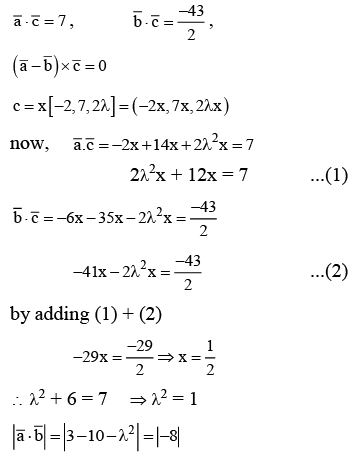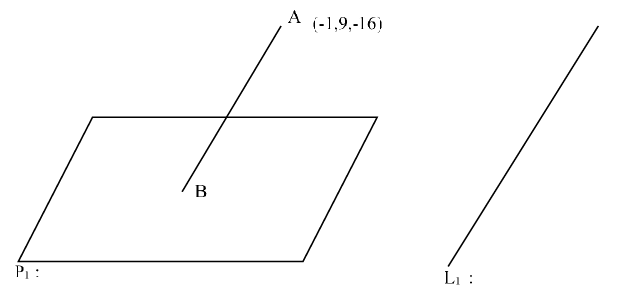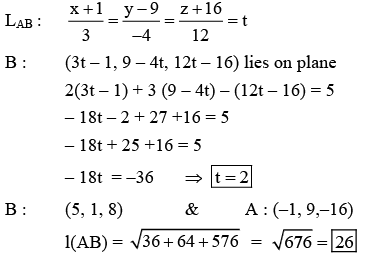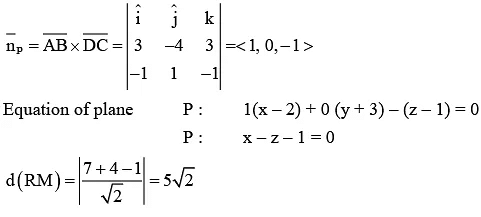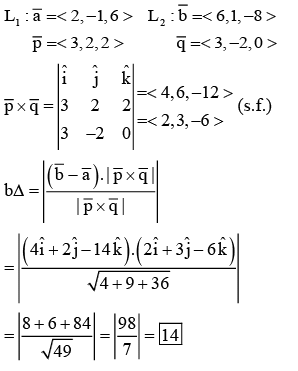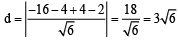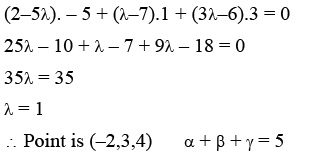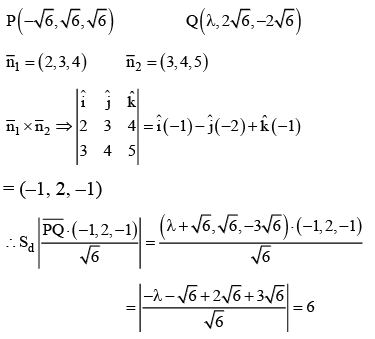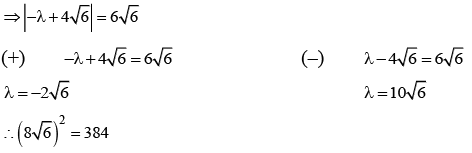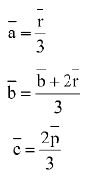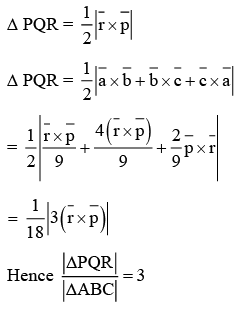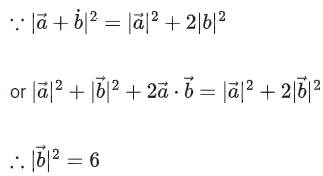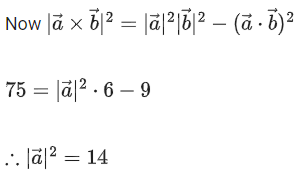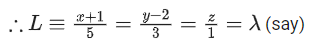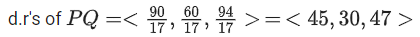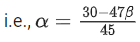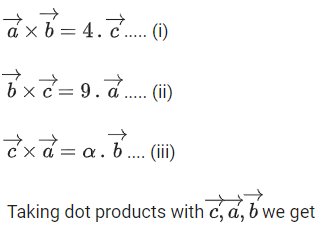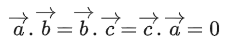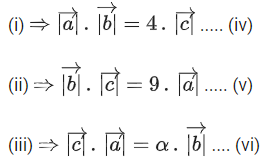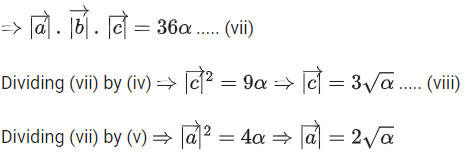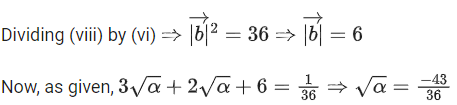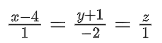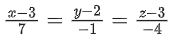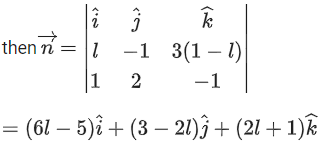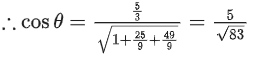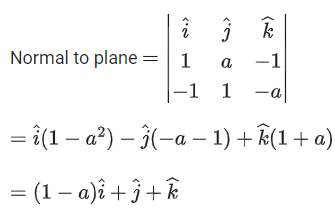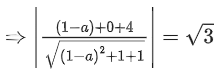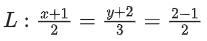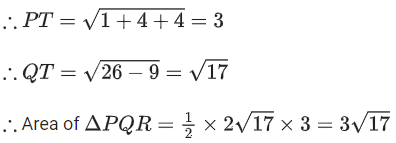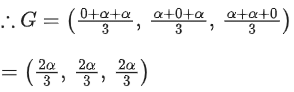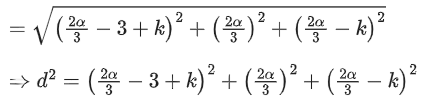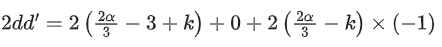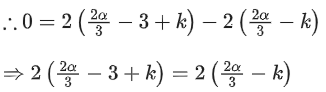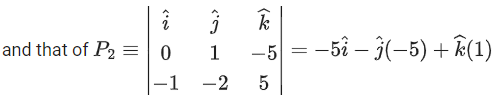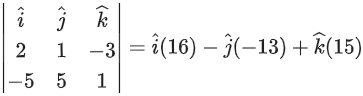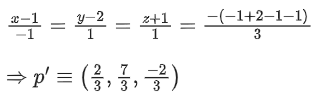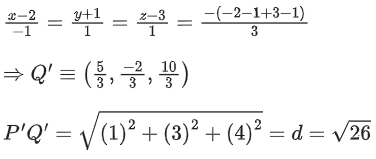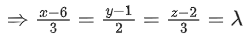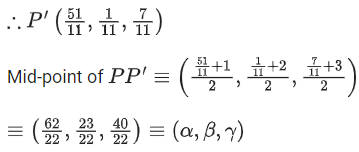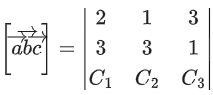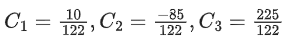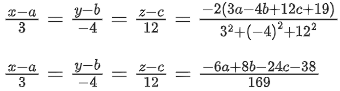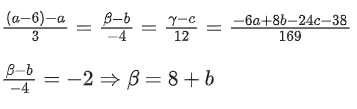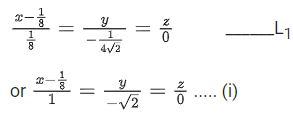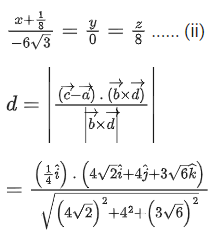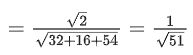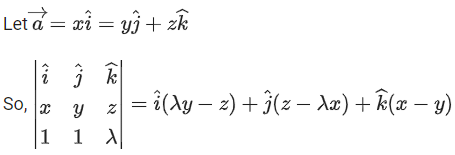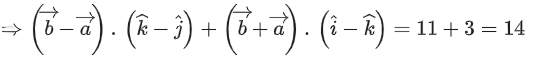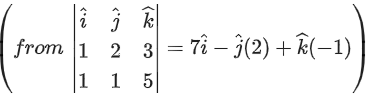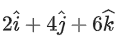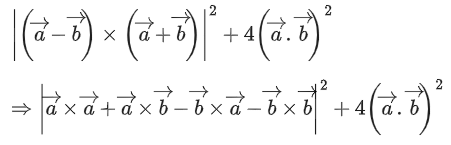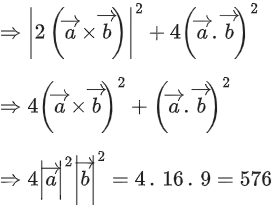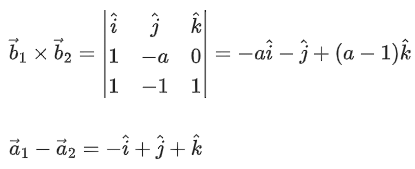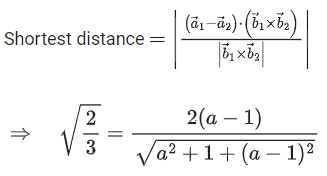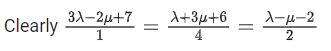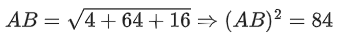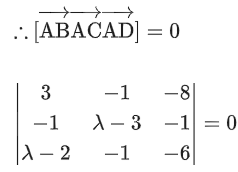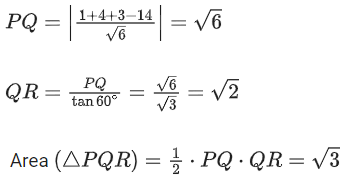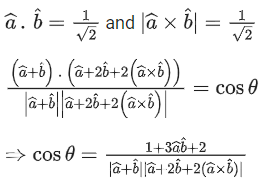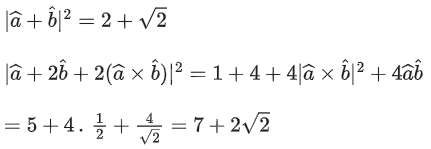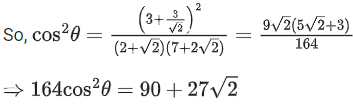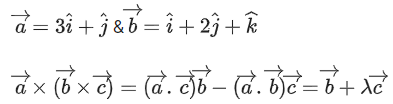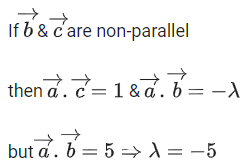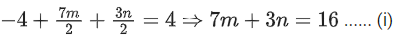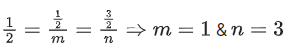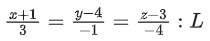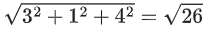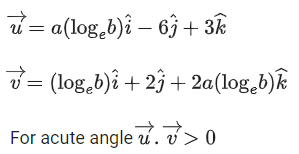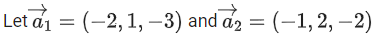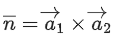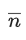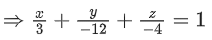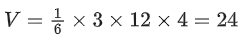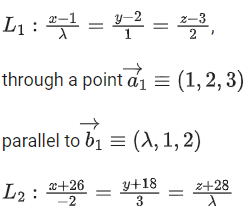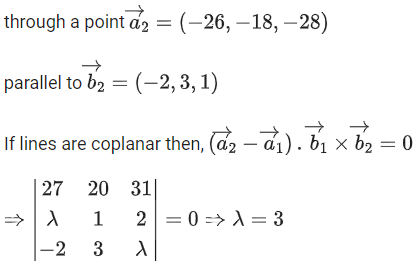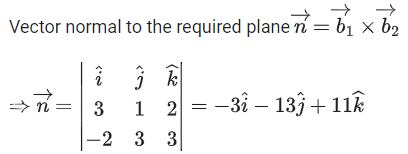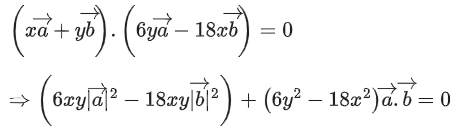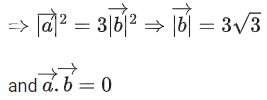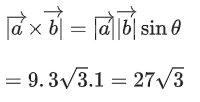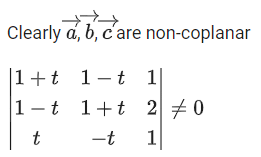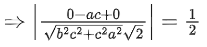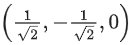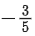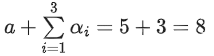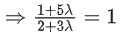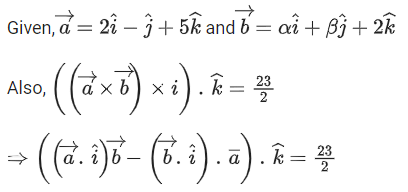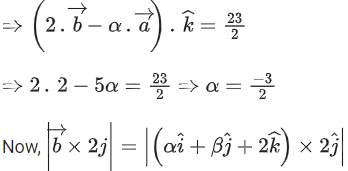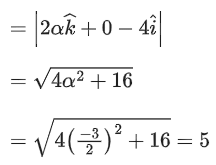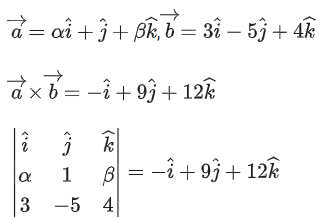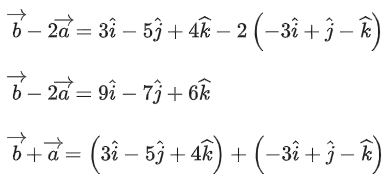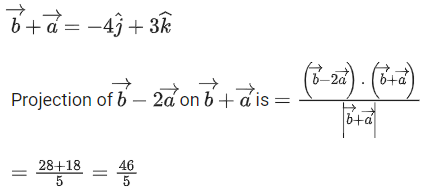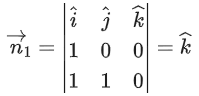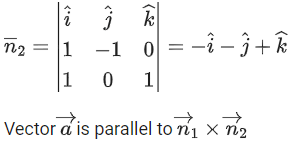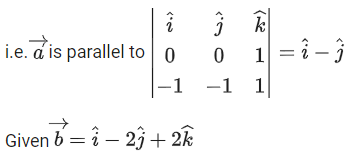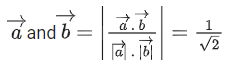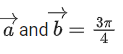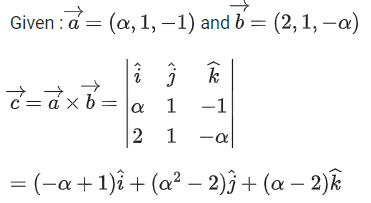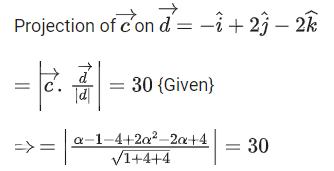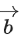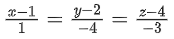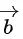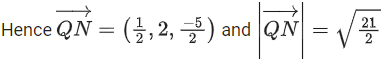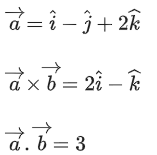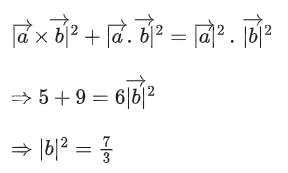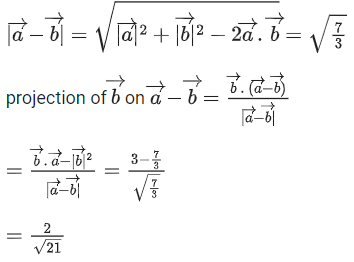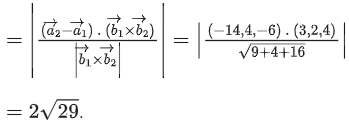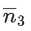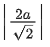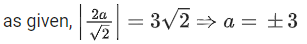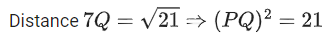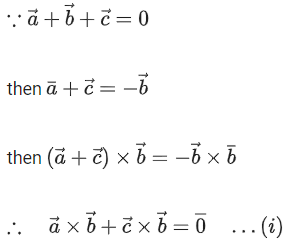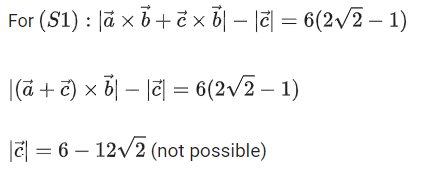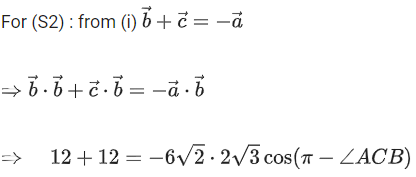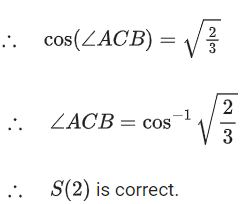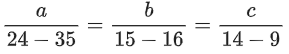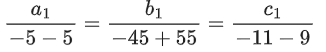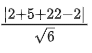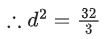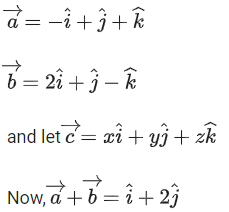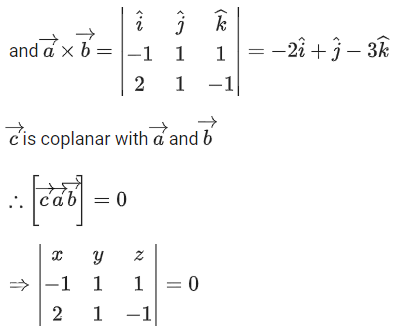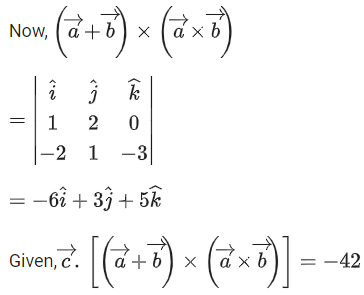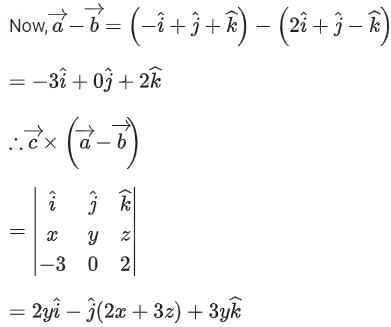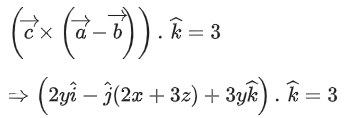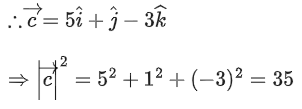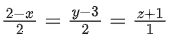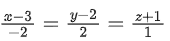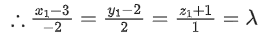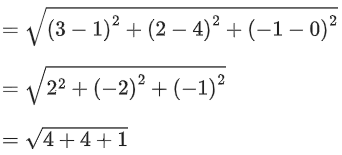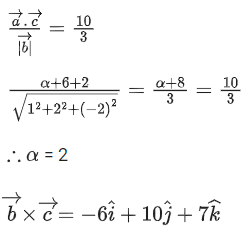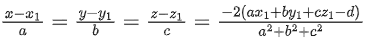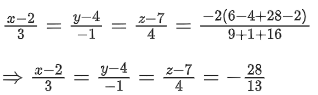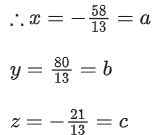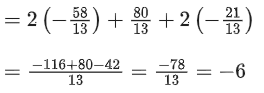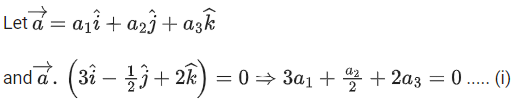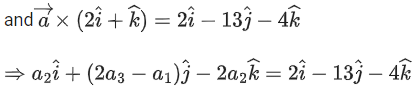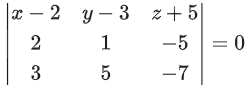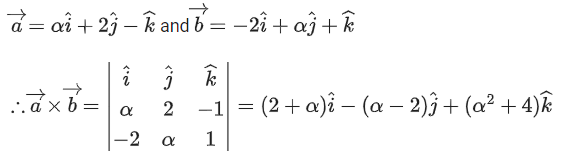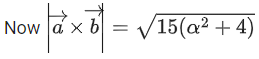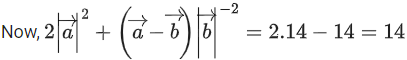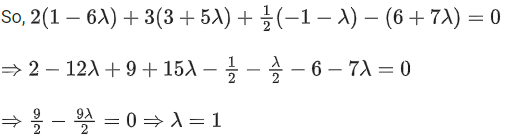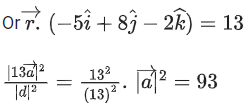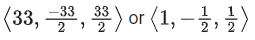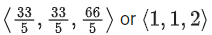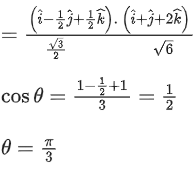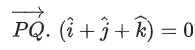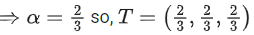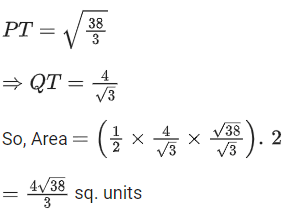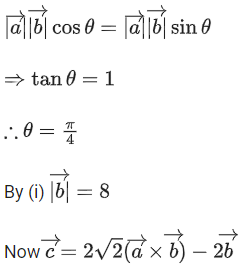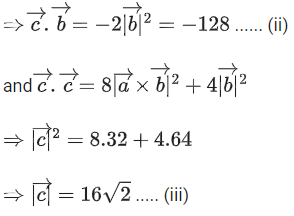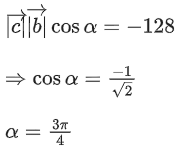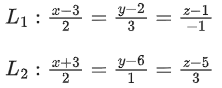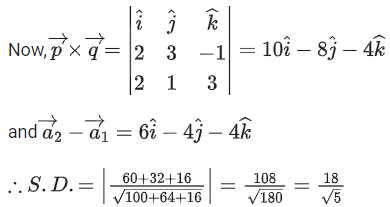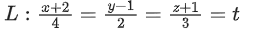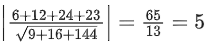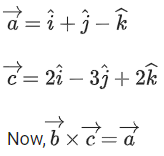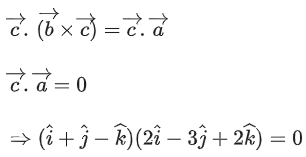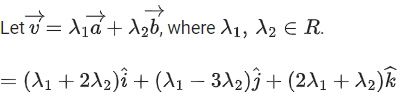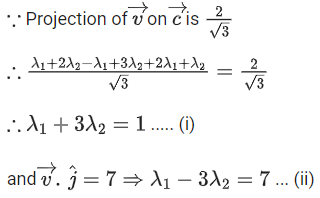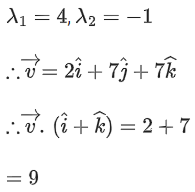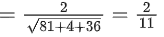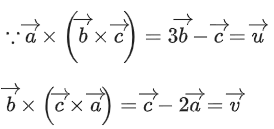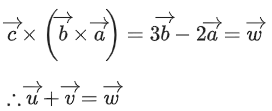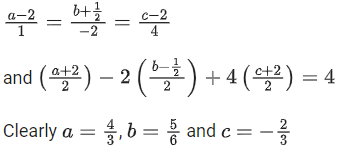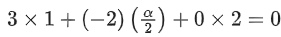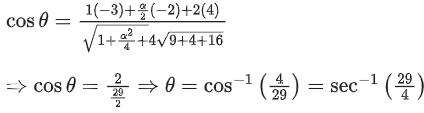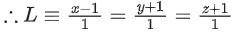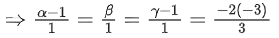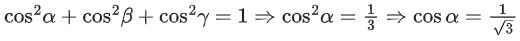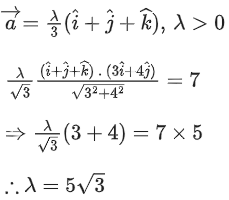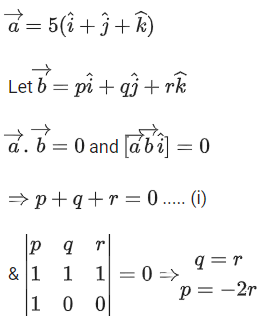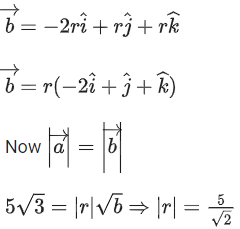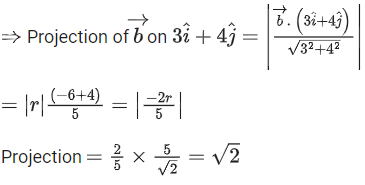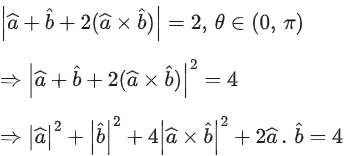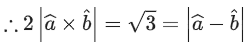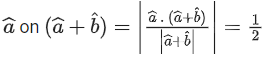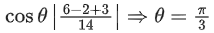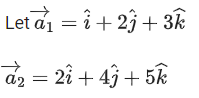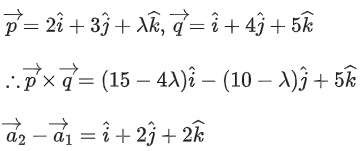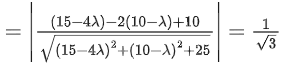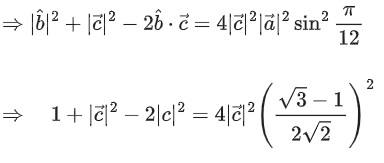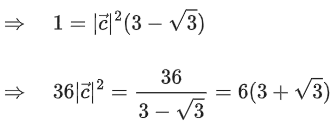Q.1. Let 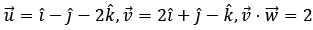 and
and 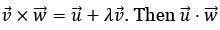 is equal to (JEE Main 2023)
is equal to (JEE Main 2023)
(a) 2
(b) 3/2
(c) 1
(d) 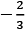
Ans. c
Q.2. Let 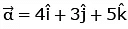 and
and 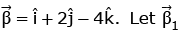 be parallel to
be parallel to 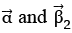 be perpendicular to
be perpendicular to 
 then the value of
then the value of 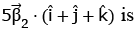 (JEE Main 2023)
(JEE Main 2023)
(a) 7
(b) 9
(c) 6
(d) 11
Ans. a
Q.3. Let 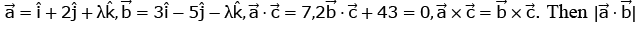 is equal to (JEE Main 2023)
is equal to (JEE Main 2023)
Ans. 8
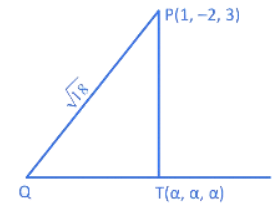
Q.4. The distance of the point (−1,9, −16) from the plane 2x + 3y − z = 5 measured parallel to the line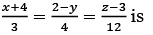 (JEE Main 2023)
(JEE Main 2023)
(a) 31
(b) 13√2
(c) 20√2
(d) 26
Ans. d
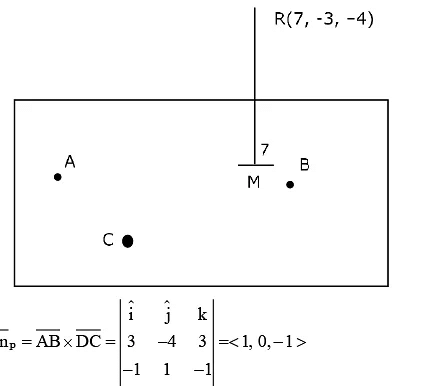
Q.5. The distance of the point (7, −3, −4) from the plane passing through the points (2, −3,1), (−1,1, −2) and (3, −4,2) is : (JEE Main 2023)
(a) 5
(b) 4
(c) 5√2
(d) 4√2
Ans. c
Q.6. The shortest distance between the lines 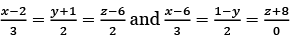 is equal to (JEE Main 2023)
is equal to (JEE Main 2023)
Ans. 14
Q.7. Let the plane containing the line of intersection of the planes P1: x + (λ + 4)y + z = 1 and P2: 2x + y + z = 2 pass through the points (0,1,0) and (1,0,1). Then the distance of the point (2λ, λ, −λ) from the plane P2 is (JEE Main 2023)
(a) 4√6
(b) 3√6
(c) 5√6
(d) 2√6
Ans. b
[x + (λ+4)y + z-1] + μ[2x+y + z- 2] =0
(0,1,0)
(i) (λ + 4 – 1) + μ[-1] = 0
λ - m = -3
(1,0,1) (ii) 1 + μ[1] = 0 ⇒ m = -1, λ = -4
∴ point (-8,-4,4); 2x + y + z - 2 = 0
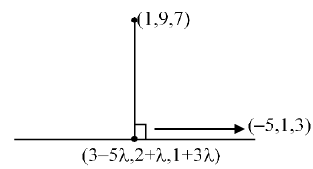
Q.8. If the foot of the perpendicular drawn from (1,9,7) to the line passing through the point (3,2,1) and parallel to the planes x + 2y + z = 0 and 3y − z = 3 is (α, β, γ), then α + β + γ is equal to (JEE Main 2023)
(a) 3
(b) 1
(c) −1
(d) 5
Ans. d
Q.9. If the shortest distance between the lines 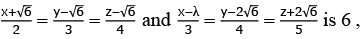 then the square of sum of all possible values of λ is (JEE Main 2023)
then the square of sum of all possible values of λ is (JEE Main 2023)
Ans. 384
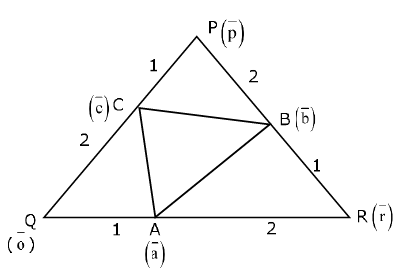
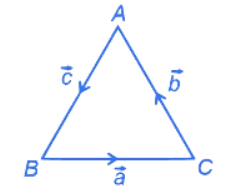
Q.10. Let PQR be a triangle. The points A, B and C are on the sides QR, RP and PQ respectively such that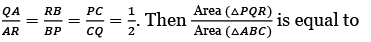 (JEE Main 2023)
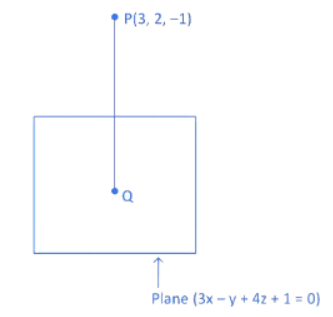
(JEE Main 2023)
(a) 4
(b) 3
(c) 2
(d) 5
Ans. b
Q.11. Let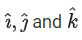 be the unit vectors along the three positive coordinate axes. Let
be the unit vectors along the three positive coordinate axes. Let 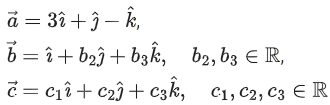
be three vectors such that b2b3>0,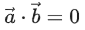 and
and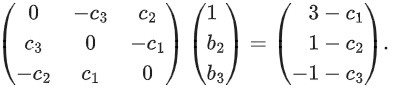
Then, which of the following is/are TRUE? (JEE Advanced 2022)
(a)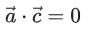
(b)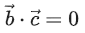
(c)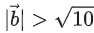
(d)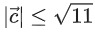
Ans. b, c, d
Q.12. Let S be the reflection of a point Q with respect to the plane given by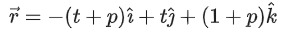
where t, p are real parameters and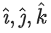 are the unit vectors along the three positive coordinate axes. If the position vectors of Q and S are
are the unit vectors along the three positive coordinate axes. If the position vectors of Q and S are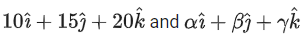 respectively, then which of the following is/are TRUE? (JEE Advanced 2022)
respectively, then which of the following is/are TRUE? (JEE Advanced 2022)
(a) 3(α + β) = −101
(b) 3(β + γ) = −71
(c) 3(γ + α) = −86
(d) 3(α + β + γ) = −121
Ans. a, b, c
Q.13. Let P1 and P2 be two planes given by
P1: 10x + 15y + 12z − 60 = 0
P2: −2x + 5y + 4z − 20 = 0
Which of the following straight lines can be an edge of some tetrahedron whose two faces lie on P1 and P2? (JEE Advanced 2022)
(a)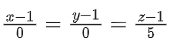
(b)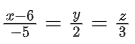
(c)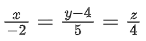
(d)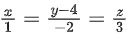
Ans. a, b, d
Q.14. Let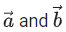 be two vectors such that
be two vectors such that Then
Then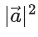 is equal to __________. (JEE Main 2022)
is equal to __________. (JEE Main 2022)
Ans. 14
Q.15. Let a line with direction ratios a, −4a, −7 be perpendicular to the lines with direction ratios 3, −1, 2b and b, a, −2. If the point of intersection of the line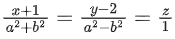 and the plane x − y + z = 0 is (α, β, γ), then α + β + γ is equal to _________. (JEE Main 2022)
and the plane x − y + z = 0 is (α, β, γ), then α + β + γ is equal to _________. (JEE Main 2022)
Ans. 10
Given a.3 + (−4a)(−1) + (−7)2b = 0 ...... (1)and ab − 4a2 + 14 = 0 ....... (2)
⇒ a2 = 4 and b2 = 1
⇒ General point on line is (5λ − 1, 3λ + 2, λ) for finding point of intersection with x − y + z = 0 we get (5λ − 1) − (3λ + 2) + (λ) = 0
⇒ 3λ − 3 = 0 ⇒ λ = 1
∴ Point at intersection (4, 5, 1)
∴ α + β + γ = 4 + 5 + 1 = 10
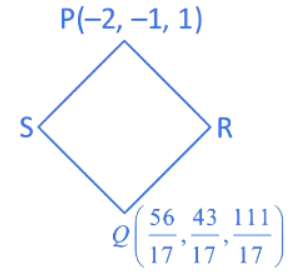
Q.16. Let P(−2,−1,1) and Q(56/17, 43/17, 111/17) be the vertices of the rhombus PRQS. If the direction ratios of the diagonal RS are α, −1, β, where both α and β are integers of minimum absolute values, then α2 + β2 is equal to ____________. (JEE Main 2022)
Ans. 450
d.r's of RS = <α, −1, β>
as PQ and RS are diagonals of rhombus
α(45) + 30(−1) + 47(β) = 0
⇒ 45α + 47β = 30
for minimum integral value α = −15 and β = 15
⇒ α2 + β2 = 450.
Q.17. Let three non-coplanar vectors such that
three non-coplanar vectors such that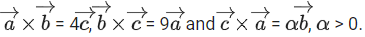 If
If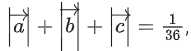 then α is equal to __________. (JEE Main 2022)
then α is equal to __________. (JEE Main 2022)
Ans. 36
Given,
Hence,
Multiplying (iv), (v) and (vi)
Q.18. Let the line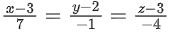 intersect the plane containing the lines
intersect the plane containing the lines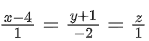 and 4ax − y + 5z − 7a = 0 = 2x − 5y − z − 3, a ∈ R at the point P(α, β, γ). Then the value of α + β + γ equals _____________. (JEE Main 2022)
and 4ax − y + 5z − 7a = 0 = 2x − 5y − z − 3, a ∈ R at the point P(α, β, γ). Then the value of α + β + γ equals _____________. (JEE Main 2022)
Ans. 12
Equation of plane containing the line 4ax − y + 5z − 7a = 0 = 2x − 5y − z − 3 can be written as
4ax − y + 5z − 7a + λ(2x − 5y − z − 3) = 0
(4a + 2λ)x − (1 + 5λ)y + (5 − λ)z − (7z + 3λ) = 0
Which is coplanar with the line
4(4a + 2λ) + (1 + 5λ) − (7a + 3λ) = 0
9a + 10λ + 1 = 0 ..... (1)
(4a + 2λ)1 + (1 + 5λ)2 + 5 − λ = 0
4a + 11λ + 7 = 0 ...... (2)
a = 1, λ = −1
Equation of plane is x + 2y + 3z − 2 = 0
Intersection with the line
(7t + 3) + 2(−t + 2) + 3(−4t + 3) − 2 = 0
−7t + 14 = 0
t = 2
So, the required point is (17, 0, −5)
α + β + γ = 12
Q.19. The plane passing through the line L: lx − y + 3(1 − l)z = 1, x + 2y − z = 2 and perpendicular to the plane 3x + 2y + z = 6 is 3x − 8y + 7z = 4. If θ is the acute angle between the line L and the y-axis, then 415cos2θ is equal to _____________. (JEE Main 2022)
Ans. 125
L: lx − y + 3(1 − l)z = 1, x + 2y − z = 2 and plane containing the line p: 3x − 8y + 7z = 4Let
be the vector parallel to L.
∵ R containing L
3(6l − 5) − 8(3 − 2l) + 7(2l + 1) = 0
18l + 16l + 14l − 15 − 24 + 7 = 0
∴ l = 32/48 = 2/3
Let θ be the acute angle between L and y-axis
∴ 415cos2θ = 125
Q.20. The largest value of a, for which the perpendicular distance of the plane containing the lines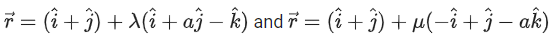 from the point (2, 1, 4) is √3, is _________. (JEE Main 2022)
from the point (2, 1, 4) is √3, is _________. (JEE Main 2022)
Ans. 20
∴ Plane (1 − a)(x − 1) + (y − 1) + z = 0Distance from (2, 1, 4) is 3 i.e.
⇒ 25 + a2 − 10a = 3a2 − 6a + 9⇒ 2a2 + 4a − 16 = 0
⇒ a2 + 2a − 8 = 0
a = 2 or −4
∴ amax = 2
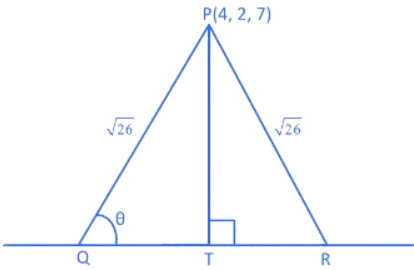
Q.21. Let Q and R be two points on the line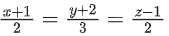 at a distance √26 from the point P(4, 2, 7). Then the square of the area of the triangle PQR is ___________. (JEE Main 2022)
at a distance √26 from the point P(4, 2, 7). Then the square of the area of the triangle PQR is ___________. (JEE Main 2022)
Ans. 153
Let T(2t − 1, 3t − 2, 2t + 1)
∵ PT ⊥r QR
∴ 2(2t − 5) + 3(3t − 4) + 2(2t − 6) = 0
17t = 34
∴ t = 2
So T(3, 4, 5)
∴ Square of ar(ΔPQR) = 153.
Q.22. The line of shortest distance between the lines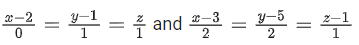 makes an angle of
makes an angle of with the plane P: ax − y − z = 0, (a > 0). If the image of the point (1, 1, −5) in the plane P is (α, β, γ), then α + β − γ is equal to _________________. (JEE Main 2022)
with the plane P: ax − y − z = 0, (a > 0). If the image of the point (1, 1, −5) in the plane P is (α, β, γ), then α + β − γ is equal to _________________. (JEE Main 2022)
Ans. 3
Wrong Question.
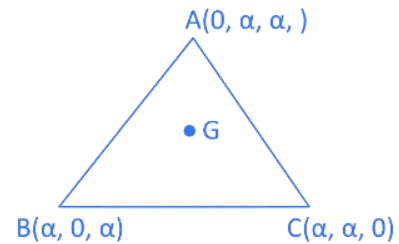
Q.23. Consider a triangle ABC whose vertices are A(0, α, α), B(α, 0, α) and C(α, α, 0), α > 0. Let D be a point moving on the line x + z − 3 = 0 = y and G be the centroid of ΔABC. If the minimum length of GD is then α is equal to ____________. (JEE Main 2022)
then α is equal to ____________. (JEE Main 2022)
Ans. 6
Given, G is the centroid of ΔABC
Also given, D is a point moving on the line x + z − 3 = 0 = yLet D = (h, 0, k)
x + z − 3 = 0 ⇒ h + k − 3 = 0 ⇒ h = 3 − k
∴ D = (3 − k, 0, k)
Now, length of GD = d
Differentiating both side with respect to k, we get
For maximum or minimum value of k, d' = 0
⇒ −3 + k = −k⇒ k = 3/2
⇒ (4α − 9)2 + 16α2 + (4α − 9)2 = 57 × 18
⇒ 16α2 − 72α + 81 + 16α2 + 16α2 − 72α + 81 = 57 × 18
⇒ 48α2 − 144α + 162 = 1026
⇒ 24α2 − 72α + 81 − 513 = 0
⇒ 24α2 − 72α − 432 = 0
⇒ α2 − 3α − 18 = 0
⇒ α2 − 6α + 3α − 18 = 0
⇒ α(α − 6) + 3(α − 6) = 0
⇒ (α − 6)(α + 3) = 0
⇒ α = 6, −3
Given, α > 0
∴ Possible value of α = 6.
Q.24. Let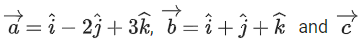 be a vector such that
be a vector such that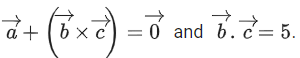 Then the value of
Then the value of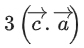 is equal to _________. (JEE Main 2022)
is equal to _________. (JEE Main 2022)
Ans. 10
Q.25. Let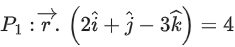 be a plane. Let P2 be another plane which passes through the points (2, −3, 2), (2, −2, −3) and (1, −4, 2). If the direction ratios of the line of intersection of P1 and P2 be 16, α, β, then the value of α + β is equal to ________________. (JEE Main 2022)
be a plane. Let P2 be another plane which passes through the points (2, −3, 2), (2, −2, −3) and (1, −4, 2). If the direction ratios of the line of intersection of P1 and P2 be 16, α, β, then the value of α + β is equal to ________________. (JEE Main 2022)
Ans. 28
Direction ratio of normal to P1 ≡ <2, 1, −3>
i.e. <−5, 5, 1>
d.r's of line of intersection are along vector
i.e. <16, 13, 15>
∴ α + β = 13 + 15 = 28
Q.26. Let d be the distance between the foot of perpendiculars of the points P(1, 2, −1) and Q(2, −1, 3) on the plane −x + y + z = 1. Then d2 is equal to ___________. (JEE Main 2022)
Ans. 26
Foot of perpendicular from P
and foot of perpendicular from Q
⇒ d2 = 26
Q.27. Let the image of the point P(1, 2, 3) in the line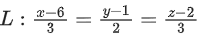 be Q. Let R (α, β, γ) be a point that divides internally the line segment PQ in the ratio 1 : 3. Then the value of 22 (α + β + γ) is equal to __________. (JEE Main 2022)
be Q. Let R (α, β, γ) be a point that divides internally the line segment PQ in the ratio 1 : 3. Then the value of 22 (α + β + γ) is equal to __________. (JEE Main 2022)
Ans. 125
The point dividing PQ in the ratio 1 : 3 will be mid-point of P & foot of perpendicular from P on the line.
∴ Let a point on line be λ
⇒ P′(3λ + 6, 2λ + 1, 3λ + 2)
as P' is foot of perpendicular
(3λ + 5)3 + (2λ − 1)2 + (3λ − 1)3 = 0
⇒ 22λ + 15 − 2 − 3 = 0
⇒ λ = −511
⇒ 22(α, β, γ) = 62 + 23 + 40 = 125
Q.28. If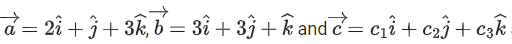 are coplanar vectors and
are coplanar vectors and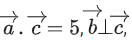 then 122(c1 + c2 + c3) is equal to ___________. (JEE Main 2022)
then 122(c1 + c2 + c3) is equal to ___________. (JEE Main 2022)
Ans. 150
2C1 + C2 + 3C3 = 5 ...... (i)
3C1 + 3C2 + C3 = 0 ...... (ii)
= 2(3C3 − C2) − 1(3C3 − C1) + 3(3C2 − 3C1)
= 3C3 + 7C2 − 8C1
⇒ 8C1 − 7C2 − 3C3 = 0 ...... (iii)
So 122(C1 + C2 + C3) = 150
Q.29. Let the mirror image of the point (a, b, c) with respect to the plane 3x − 4y + 12z + 19 = 0 be (a − 6, β, γ). If a + b + c = 5, then 7β − 9γ is equal to ______________. (JEE Main 2022)
Ans. 137
(x, y, z) ≡ (a − 6, β, γ)
⇒ 3a − 4b + 12c = 150 ..... (1)
a + b + c = 5
3a + 3b + 3c = 15 ...... (2)
Applying (1) - (2)
−7b + 9c = 135
7b − 9c = −135
7β − 9γ = 7(8 + b) − 9(−24 + c)
= 56 + 216 + 7b − 9c
= 56 + 216 − 135 = 137
Q.30. Let l1 be the line in xy-plane with x and y intercepts 1/8 and 1/4√2 respectively, and l2 be the line in zx-plane with x and z intercepts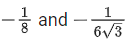 respectively. If d is the shortest distance between the line l1 and l2, then d−2 is equal to _______________. (JEE Main 2022)
respectively. If d is the shortest distance between the line l1 and l2, then d−2 is equal to _______________. (JEE Main 2022)
Ans. 51
Equation of L2
d−2 = 51
Q.31. Let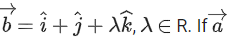 is a vector such that
is a vector such that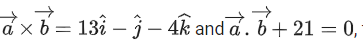 then
then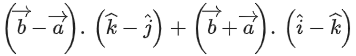 is equal to _____________. (JEE Main 2022)
is equal to _____________. (JEE Main 2022)
Ans. 14
⇒ λy − z = 13, z − λx = −1, x − y = −4
and x + y + λz = −21
⇒ Clearly, λ = 3, x = −2, y = 2 and z = −7
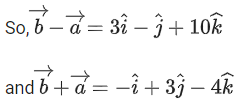
Q.32. Let the lines

intersect at the point S. If a plane ax + by − z + d = 0 passes through S and is parallel to both the lines L1 and L2, then the value of a + b + d is equal to ____________. (JEE Main 2022)
Ans. 5
As plane is parallel to both the lines we have d.r's of normal to the plane as <7, −2, −1>
Also point of intersection of lines is
∴ Equation of plane is
7(x − 2) − 2(y − 4) − 1(z − 6) = 0
⇒ 7x − 2y − z = 0
a + b + d = 7 − 2 + 0 = 5
Q.33. Let θ be the angle between the vectors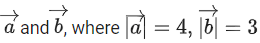 and θ ∈ (π/4, π/3). Then
and θ ∈ (π/4, π/3). Then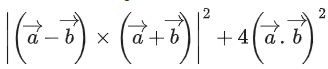 is equal to __________. (JEE Main 2022)
is equal to __________. (JEE Main 2022)
Ans. 576
Q.34. If the shortest distance between the lines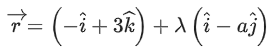 and
and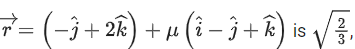 then the integral value of a is equal to ___________. (JEE Main 2022)
then the integral value of a is equal to ___________. (JEE Main 2022)
Ans. 2
⇒ 6(a2 − 2a + 1) = 2a2 − 2a + 2
⇒ (a − 2)(2a − 1) = 0 ⇒ a = 2 because a ∈ z.
Q.35. Let a line having direction ratios, 1, −4, 2 intersect the lines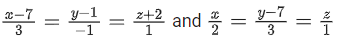 at the points A and B. Then (AB)2 is equal to ___________. (JEE Main 2022)
at the points A and B. Then (AB)2 is equal to ___________. (JEE Main 2022)
Ans. 84
Let A(3λ + 7, −λ + 1, λ − 2) and B(2μ, 3μ + 7, μ)
So, DR's of AB ∝ 3λ − 2μ + 7, −(λ + 3μ + 6), λ − μ − 2
⇒ 5λ − 3μ = −16
And λ − 5μ = 10
From (i) and (ii) we get λ = −5, μ = −3
So, A is (−8, 6, −7) and B is (−6, −2, −3)
Q.36. Let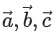 be three coplanar concurrent vectors such that angles between any two of them is same. If the product of their magnitudes is 14 and
be three coplanar concurrent vectors such that angles between any two of them is same. If the product of their magnitudes is 14 and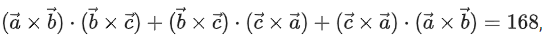 then
then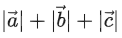 is equal to: (JEE Main 2022)
is equal to: (JEE Main 2022)
(a) 10
(b) 14
(c) 16
(d) 18
Ans. c
Q.37. If (2, 3, 9), (5, 2, 1), (1, λ, 8) and (λ, 2, 3) are coplanar, then the product of all possible values of λ is: (JEE Main 2022)
(a) 21/2
(b) 59/8
(c) 57/8
(d) 95/8
Ans. d
∵ A(2, 3, 9), B(5, 2, 1), C(1, λ, 8) and D(λ, 2, 3) are coplanar.
⇒ [−6(λ − 3) − 1] − 8(1 − (λ − 3)(λ − 2)) + (6 + (λ − 2) = 0
⇒ 3(−6λ + 17) − 8(−λ2 + 5λ − 5) + (λ + 4) = 8
⇒ 8λ2 − 57λ + 95 = 0
∴ λ1λ2 = 95/8
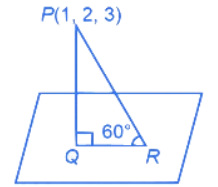
Q.38. Let Q be the foot of perpendicular drawn from the point P(1, 2, 3) to the plane x + 2y + z = 14. If R is a point on the plane such that ∠PRQ = 60∘, then the area of △PQR is equal to: (JEE Main 2022)
(a) √3/2
(b) √3
(c) 2√3
(d) 3
Ans. b
Q.39. Let be two unit vectors such that the angle between them is π/4. If θ is the angle between the vectors
be two unit vectors such that the angle between them is π/4. If θ is the angle between the vectors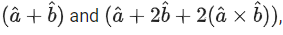 then the value of 164 cos2θ is equal to: (JEE Main 2022)
then the value of 164 cos2θ is equal to: (JEE Main 2022)
(a) 90 + 27√2
(b) 45 + 18√2
(c) 90 + 3√2
(d) 54 + 90√2
Ans. a
Q.40. Let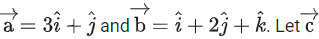 be a vector satisfying
be a vector satisfying 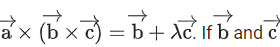 are non-parallel, then the value of λ is: (JEE Main 2022)
are non-parallel, then the value of λ is: (JEE Main 2022)
(a) −5
(b) 5
(c) 1
(d) −1
Ans. a
Q.41. If the foot of the perpendicular from the point A(−1, 4, 3) on the plane P: 2x + my + nz = 4, is (−2, 7/2, 3/2), then the distance of the point A from the plane P, measured parallel to a line with direction ratios 3, −1, −4, is equal to: (JEE Main 2022)
(a) 1
(b) √26
(c) 2√2
(d) √14
Ans. b
(−2, 7/2, 3/2) satisfies the plane P: 2x + my + nz = 4
Line joining A(−1, 4, 3) and (−2, 7/2, 3/2) is perpendicular to P: 2x + my + nz = 4
Plane P: 2x + y + 3z = 4
Distance of P from A(−1, 4, 3) parallel to the line
for point of intersection of P & L
2(3r − 1) + (−r + 4) + 3(−4r + 3) = 4 ⇒ r = 1
Point of intersection: (2, 3, −1)
Required distance
Q.42. Let S be the set of all a ∈ R for which the angle between the vectors  and
and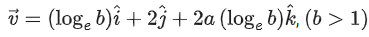 is acute. Then S is equal to: (JEE Main 2022)
is acute. Then S is equal to: (JEE Main 2022)
(a)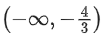
(b) Φ
(c)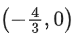
(d) (12/7, ∞)
Ans. b
⇒ a(logeb)2 − 12 + 6a(logeb) > 0
∵ b > 1
Let logeb = t ⇒ t > 0 as b > 1
at2 + 6at − 12 > 0∀t > 0
⇒ a ∈ ϕ
Q.43. A plane P is parallel to two lines whose direction ratios are −2, 1, −3 and −1, 2, −2 and it contains the point (2, 2, −2). Let P intersect the co-ordinate axes at the points A, B, C making the intercepts α, β, γ. If V is the volume of the tetrahedron OABC, where O is the origin, and p = α + β + γ, then the ordered pair (V, p) is equal to: (JEE Main 2022)
(a) (48, −13)
(b) (24, −13)
(c) (48, 11)
(d) (24, −5)
Ans. b
Vector normal to plane
= (4, −1, −3)
Plane through (2, 2, −2) and normal to
(x − 2, y − 2, z + 2) . (4, −1, −3) = 0
⇒ 4x − y − 3z = 12
Intercepts α, β, γ are 3, −12, −4
P = α + β + γ = −13
Q.44. Let the lines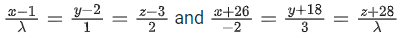 be coplanar and P be the plane containing these two lines. Then which of the following points does NOT lie on P? (JEE Main 2022)
be coplanar and P be the plane containing these two lines. Then which of the following points does NOT lie on P? (JEE Main 2022)
(a) (0,−2,−2)
(b) (−5,0,−1)
(c) (3,−1,0)
(d) (0,4,5)
Ans. d
Equation of plane≡ ((x − 1), (y − 2), (z − 3)) . (−3, −13, 11) = 0
⇒ 3x + 13y − 11z + 4 = 0
Checking the option gives (0, 4, 5) does not lie on the plane.
Q.45. Let a vector has magnitude 9. Let a vector
has magnitude 9. Let a vector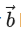 be such that for every (x, y) ∈ R × R − {(0, 0)}, the vector
be such that for every (x, y) ∈ R × R − {(0, 0)}, the vector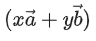 is perpendicular to the vector
is perpendicular to the vector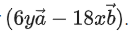 Then the value of
Then the value of 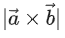 is equal to: (JEE Main 2022)
is equal to: (JEE Main 2022)
(a) 9√3
(b) 27√3
(c) 9
(d) 81
Ans. b
As given equation is identityCoefficient of x2 = coefficient of y2 = coefficient of xy = 0
Q.46. Let the vectors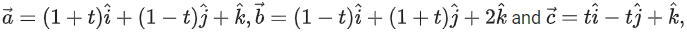 t ∈ R be such that for α, β, γ ∈ R,
t ∈ R be such that for α, β, γ ∈ R,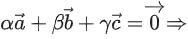 α = β = γ = 0. Then, the set of all values of t is: (JEE Main 2022)
α = β = γ = 0. Then, the set of all values of t is: (JEE Main 2022)
(a) a non-empty finite set
(b) equal to N
(c) equal to R−{0}
(d) equal to R
Ans. c
⇒ (1 + t)(1 + t + 2t) − (1 − t)(1 − t − 2t) + 1(t2 − t − t − t2) ≠ 0⇒ (3t2 + 4t + 1) − (1 − t)(1 − 3t) − 2t ≠ 0
⇒ (3t2 + 4t + 1) − (3t2 − 4t + 1) − 2t ≠ 0
⇒ t ≠ 0
Q.47. If the line of intersection of the planes ax + by = 3 and ax + by + cz = 0, a > 0 makes an angle 30∘ with the plane y − z + 2 = 0, then the direction cosines of the line are: (JEE Main 2022)
(a)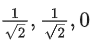
(b)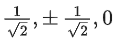
(c)
(d)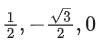
Ans. b
P1: ax + by + 0z = 3, normal vector:= (a, b, 0)
P2: ax + by + cz = 0, normal vector:
= (a, b, c)
Vector parallel to the line of intersection =
= (bc, −ac, 0)
Vector normal to 0 . x + y − z + 2 = 0 is
= (0, 1, −1)
Angle between line and plane is 30∘
⇒ a2 = b2
Hence,
= (ac, −ac, 0)
Direction ratios =
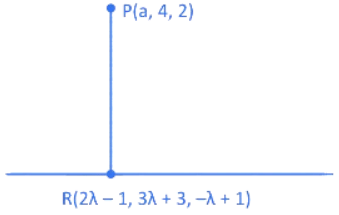
Q.48. If the length of the perpendicular drawn from the point P(a, 4, 2), a > 0 on the line 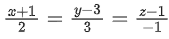 is 2√6 units and Q(α1, α2, α3) is the image of the point P in this line, then
is 2√6 units and Q(α1, α2, α3) is the image of the point P in this line, then 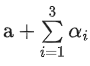 is equal to: (JEE Main 2022)
is equal to: (JEE Main 2022)
(a) 7
(b) 8
(c) 12
(d) 14
Ans. b
∵ PR is perpendicular to given line, so
2(2λ − 1 − a) + 3(3λ − 1) − 1(−λ − 1) = 0⇒ a = 7λ − 2
Now,
∵ PR = 2√6
⇒ (−5λ + 1)2 + (3λ − 1)2 + (λ + 1)2 = 24
⇒ 5λ2 − 2λ − 3 = 0 ⇒ λ = 1 or
∵ a > 0 so λ = 1 and a = 5
Now
(Sum of co-ordinate of R) − (Sum of coordinates of P)
= 2(7) − 11 = 3
Q.49. If the plane P passes through the intersection of two mutually perpendicular planes 2x + ky − 5z = 1 and 3kx − ky + z = 5, k < 3 and intercepts a unit length on positive x-axis, then the intercept made by the plane P on the y-axis is (JEE Main 2022)
(a) 1/11
(b) 5/11
(c) 6
(d) 7
Ans. d
P1: 2x + ky − 5z = 1P2: 3kx − ky + z = 5
∵ P1 ⊥ P2 ⇒ 6k − k2 + 5 = 0
⇒ k = 1, 5
∵ k < 3
∴ k = 1
P1: 2x + y − 5z = 1
P2: 3x − y + z = 5
P: (2x + y − 5z − 1) + λ(3x − y + z − 5) = 0
Positive x-axis intercept = 1
⇒ λ = 12
∴ P: 7x + y − 4z = 7
y intercept = 7.
Q.50. Let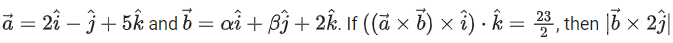 is equal to (JEE Main 2022)
is equal to (JEE Main 2022)
(a) 4
(b) 5
(c) 21
(d) 17
Ans. b
Q.51. Let be two vectors, such that
be two vectors, such that 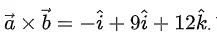 Then the projection of
Then the projection of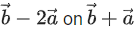 is equal to (JEE Main 2022)
is equal to (JEE Main 2022)
(a) 2
(b) 39/5
(c) 9
(d) 46/5
Ans. d
4 + 5β = −1 ⇒ β = −1−5α − 3 = 12 ⇒ α = −3
Q.52. A vector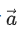 is parallel to the line of intersection of the plane determined by the vectors
is parallel to the line of intersection of the plane determined by the vectors 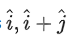 and the plane determined by the vectors
and the plane determined by the vectors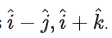 The obtuse angle between
The obtuse angle between  and the vector
and the vector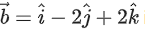 is (JEE Main 2022)
is (JEE Main 2022)
(a) 3π/4
(b) 2π/3
(c) 4π/5
(d) 5π/6
Ans. a
Ifis a vector normal to the plane determined by
then
If
is a vector normal to the plane determined by
then
Cosine of acute angle between
Obtuse angle between
Q.53. Let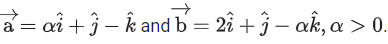 If the projection of
If the projection of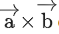 on the vector
on the vector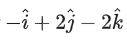 is 30, then α is equal to: (JEE Main 2022)
is 30, then α is equal to: (JEE Main 2022)
(a) 15/2
(b) 8
(c) 13/2
(a) 7
Ans. d
On solving α = −13/2 (Rejected as α > 0)
and α = 7
Q.54. The length of the perpendicular from the point (1, −2, 5) on the line passing through (1, 2, 4) and parallel to the line x + y − z = 0 = x − 2y + 3z − 5 is: (JEE Main 2022)
(a)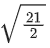
(b)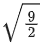
(c)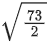
(d) 1
Ans. a
The line x + y − z = 0 = x − 2y + 3z − 5 is parallel to the vector
Equation of the line through P(1, 2, 4) and parallel to
Let N ≡ (λ + 1, −4λ + 2, −3λ + 4)
= (λ, −4λ + 4, −3λ − 1)
is perpendicular to
⇒ (λ, −4λ + 4, −3λ − 1) . (1, 4, −3) = 0
⇒ λ = 1/2
Q.55. Let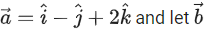 be a vector such that
be a vector such that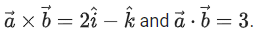 Then the projection of
Then the projection of on the vector
on the vector 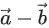 is: (JEE Main 2022)
is: (JEE Main 2022)
(a)
(b)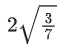
(c)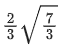
(d) 2/3
Ans. a
Q.56. The shortest distance between the lines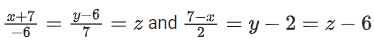 is (JEE Main 2022)
is (JEE Main 2022)
(a)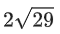
(b) 1
(c)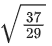
(d)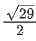
Ans. a
Shortest distance between L1 and L2
Q.57. A plane E is perpendicular to the two planes 2x − 2y + z = 0 and x − y + 2z = 4, and passes through the point P(1, −1, 1). If the distance of the plane E from the point Q(a, a, 2) is 3√2, then (PQ)2 is equal to (JEE Main 2022)
(a) 9
(b) 12
(c) 21
(d) 33
Ans. c
First plane, P1 = 2x − 2y + z = 0, normal vector ≡=(2,−2,1)
Second plane, P2 ≡ x − y + 2z = 4, normal vector ≡
=(1,−1,2)
Plane perpendicular to P1 and P2 will have normal vector
Equation of plane E through P(1, −1, 1) and
as normal vector
(x − 1, y + 1, z − 1) . (−3, −3, 0) = 0
⇒ x + y = 0 ≡ E
Distance of PQ(a, a, 2) from E =
Hence, Q ≡ (±3, ±3, 2)
Q.58. Let ABC be a triangle such that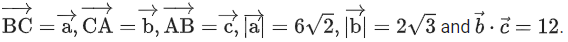 Consider the statements:
Consider the statements:
Then (JEE Main 2022)
(a) both (S1) and (S2) are true
(b) only (S1) is true
(c) only (S2) is true
(d) both (S1) and (S2) are false
Ans. c
Hence (S1) is not correct
Q.59. Let P be the plane containing the straight line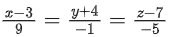 and perpendicular to the plane containing the straight lines
and perpendicular to the plane containing the straight lines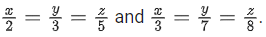 If d is the distance of P from the point (2, −5, 11), then d2 is equal to: (JEE Main 2022)
If d is the distance of P from the point (2, −5, 11), then d2 is equal to: (JEE Main 2022)
(a) 147/2
(b) 96
(c) 32/3
(d) 54
Ans. c
Let ⟨a, b, c⟩ be direction ratios of plane containing
∴ 2a + 3b + 5c = 0… (i)
and 3a + 7b + 8c = 0… (ii)
from eq. (i) and (ii):
∴ D.RS. of plane are <11, 1, −5>
Let D.RS of plane P be <a1, b1, c1> then.
11a1 + b1 − 5c1 = 0
and 9a1 − b1 − 5c1 = 0
From eq. (iii) and (iv):
∴ D.A 5. of plane P are <1, −1, 2>
Equation plane P is: 1(x − 3) − 1(y + 4) + 2(z − 7) = 0
⇒ x − y + 2z − 21 = 0
Distance from point (2, −5, 11) is d =
Q.60. Let a vector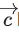 be coplanar with the vectors
be coplanar with the vectors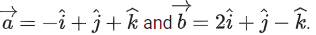 If the vector
If the vector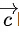 also satisfies the conditions
also satisfies the conditions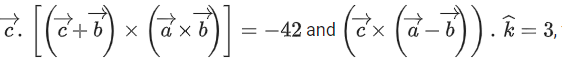 then the value of
then the value of 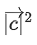 is equal to: (JEE Main 2022)
is equal to: (JEE Main 2022)
(a) 24
(b) 29
(c) 35
(d) 42
Ans. c
Given,
⇒ x(−2) − y(−1) + z(−3) = 0⇒ −2x + y − 3z = 0 ..... (1)
Given,
⇒ 3y = 3⇒ y = 1
Putting value of y = 1 in equation (1) and (2) we get,
−2x + 1 − 3z = 0 ..... (3)
and −6x + 3 + 5z = −42
⇒ −6x + 5z = −45 ..... (4)
Solving (3) and (4), we get
x = 5 and z = -3
Q.61. The distance of the point (3, 2, −1) from the plane 3x − y + 4z + 1 = 0 along the line 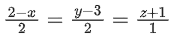 is equal to: (JEE Main 2022)
is equal to: (JEE Main 2022)
(a) 9
(b) 6
(c) 3
(d) 2
Ans. c
Line PQ is parallel to line∴ DR of PQ = DR of line = <−2, 2, 1>
∴ Equation of line PQ passing through P(3, 2, −1) and DR = <−2, 2, 1> is
Any General point on line PQ = (x1, y1, z1)
⇒ x1 = −2λ + 3
y1 = 2λ + 2
z1 = λ − 1
∴ Point Q = (−2λ + 3, 2λ + 2, λ − 1)
Point Q lies on the plane 3x − y + 4z + 1 = 0. So point Q satisfy the equation.
3(−2λ + 3) − (2λ + 2) + 4(λ − 1) + 1 = 0
⇒ −6λ + 9 − 2λ − 2 + 4λ − 4 + 1 = 0
⇒ −4λ + 4 = 0
⇒ λ = 1
∴ Point Q = (−2 × 1 + 3, 2 × 1 + 2, 1 − 1)
= (1, 4, 0)
∴ Distance of the point P(3, 2, −1) from the plane = Length of PQ
= √9
= 3
Q.62. Let A, B, C be three points whose position vectors respectively are
If α is the smallest positive integer for which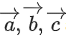 are noncollinear, then the length of the median, in ΔABC, through A is: (JEE Main 2022)
are noncollinear, then the length of the median, in ΔABC, through A is: (JEE Main 2022)
(a)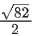
(b)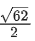
(c)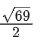
(d)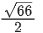
Ans. a
Q.63. Let Q be the mirror image of the point P(1, 2, 1) with respect to the plane x + 2y + 2z = 16. Let T be a plane passing through the point Q and contains the line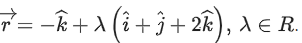 Then, which of the following points lies on T? (JEE Main 2022)
Then, which of the following points lies on T? (JEE Main 2022)
(a) (2, 1, 0)
(b) (1, 2, 1)
(c) (1, 2, 2)
(d) (1, 3, 2)
Ans. b
Q.64. Let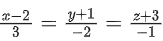 lie on the plane px − qy + z = 5, for some p, q ∈ R. The shortest distance of the plane from the origin is: (JEE Main 2022)
lie on the plane px − qy + z = 5, for some p, q ∈ R. The shortest distance of the plane from the origin is: (JEE Main 2022)
(a)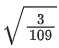
(b)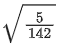
(c)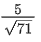
(d)
Ans. b
Q.65. Let 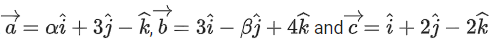 where α, β ∈ R, be three vectors. If the projection of
where α, β ∈ R, be three vectors. If the projection of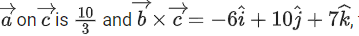 then the value of α + β is equal to: (JEE Main 2022)
then the value of α + β is equal to: (JEE Main 2022)
(a) 3
(b) 4
(c) 5
(d) 6
Ans. a
2β − 8 = −6 & 6 + β = 7
∴ β = 1
α + β = 2 + 1 = 3
Q.66. If the mirror image of the point (2, 4, 7) in the plane 3x − y + 4z = 2 is (a, b, c), then 2a + b + 2c is equal to: (JEE Main 2022)
(a) 54
(b) 50
(c) −6
(d) −42
Ans. c
We know mirror image of point (x1, y1, z1) in the plane ax + by + cz = d
Here given point (2, 4, 7) and plane 3x − y + 4z = 2 then mirror image is
∴ 2a + b + 2c
Q.67. Let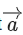 be a vector which is perpendicular to the vector
be a vector which is perpendicular to the vector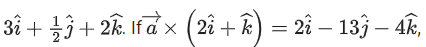 then the projection of the vector
then the projection of the vector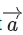 on the vector
on the vector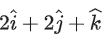 is: (JEE Main 2022)
is: (JEE Main 2022)
(a) 1/3
(b) 1
(c) 5/3
(d) 7/3
Ans. c
∴ a2 = 2 ..... (ii)and a1 − 2a3 = 13 ..... (iii)
From eq. (i) and (iii): a1 = 3 and a3 = −5
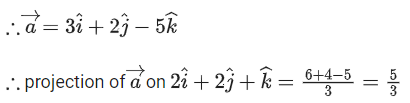
Q.68. Let the plane ax + by + cz = d pass through (2, 3, −5) and is perpendicular to the planes 2x + y − 5z = 10 and 3x + 5y − 7z = 12. If a, b, c, d are integers d > 0 and gcd (|a|, |b|, |c|, d) = 1, then the value of a + 7b + c + 20d is equal to: (JEE Main 2022)
(a) 18
(b) 20
(c) 24
(d) 22
Ans. d
Equation of pane through point (2, 3, −5) and perpendicular to planes 2x + y − 5z = 10 and 3x + 5y − 7z = 12 is
∴ Equation of plane is (x − 2)(−7 + 25) − (y − 3)
(−14 + 15) + (z + 5) . 7 = 0
∴ 18x − y + 7z + 2 = 0
⇒ 18x − y + 7z = −2
∴ −18x + y − 7z = 2
On comparing with ax + by + cz = d where d > 0 is a = − 18, b = 1, c = − 7, d = 2
∴ a + 7b + c + 20d = 22
Q.69. Let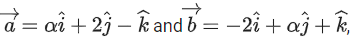 where α ∈ R. If the area of the parallelogram whose adjacent sides are represented by the vectors
where α ∈ R. If the area of the parallelogram whose adjacent sides are represented by the vectors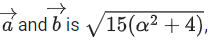 then the value of
then the value of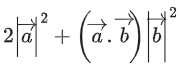 is equal to: (JEE Main 2022)
is equal to: (JEE Main 2022)
(a) 10
(b) 7
(c) 9
(d) 14
Ans. d
⇒ (2 + α)2 + (α − 2)2 + (α2 + 4)2 = 15(α2 + 4)⇒ α4 − 5α2 − 36 = 0
∴ α = ±3
Q.70. Let the plane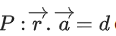 contain the line of intersection of two planes
contain the line of intersection of two planes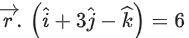 and
and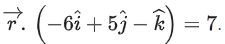 If the plane P passes through the point (2, 3, 1/2), then the value of
If the plane P passes through the point (2, 3, 1/2), then the value of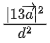 is equal to (JEE Main 2022)
is equal to (JEE Main 2022)
(a) 90
(b) 93
(c) 95
(d) 97
Ans. b
P1: x + 3y − z = 6
P2: −6x + 5y − z = 7
Family of planes passing through line of intersection of P1 and P2 is given by
x(1 − 6λ) + y(3 + 5λ) + z(−1 − λ) − (6 + 7λ) = 0It passes through (2, 3, 1/2)
Required plane is
−5x + 8y − 2z − 13 = 0
Q.71. The acute angle between the planes P1 and P2, when P1 and P2 are the planes passing through the intersection of the planes 5x + 8y + 13z − 29 = 0 and 8x − 7y + z − 20 = 0 and the points (2, 1, 3) and (0, 1, 2), respectively, is (JEE Main 2022)
(a) π/3
(b) π/4
(c) π/6
(d) π/12
Ans. a
Family of Plane's equation can be given by(5 + 8λ)x + (8 − 7λ)y + (13 + λ)z − (29 + 20λ) = 0
P1 passes through (2, 1, 3)
⇒ (10 + 16λ) + (8 − 7λ) + (39 + 3λ) − (29 + 20λ) = 0
⇒ −8λ + 28 = 0 ⇒ λ = 7/2
d.r, s of normal to P1
P2 passes through (0, 1, 2)
⇒ 8 − 7λ + 26 + 2λ − (29 + 20λ) = 0
⇒ 5 − 25λ = 0
⇒ λ = 1/5
d.r, s of normal to P2
Angle between normals
Q.72. If two distinct point Q, R lie on the line of intersection of the planes −x + 2y − z = 0 and 3x − 5y + 2z = 0 and PQ = PR = √18 where the point P is (1, −2, 3), then the area of the triangle PQR is equal to (JEE Main 2022)
(a)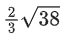
(b)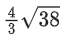
(c)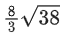
(d)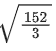
Ans. b
Line L is x = y = z
⇒ (α − 3) + α + 2 + α − 1 = 0
Q.73. Let be the vectors along the diagonals of a parallelogram having area 2√2. Let the angle between
be the vectors along the diagonals of a parallelogram having area 2√2. Let the angle between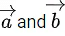 be acute,
be acute,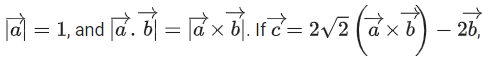 then an angle between
then an angle between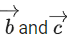 is (JEE Main 2022)
is (JEE Main 2022)
(a) π/4
(b)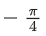
(c) 5π/6
(d) 3π/4
Ans. d
∵be the vectors along the diagonals of a parallelogram having area 2√2.
From (ii) and (iii)
Q.74. The shortest distance between the lines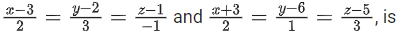 (JEE Main 2022)
(JEE Main 2022)
(a)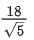
(b)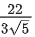
(c)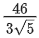
(d)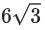
Ans. a
Q.75. Let the foot of the perpendicular from the point (1, 2, 4) on the line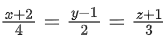 be P. Then the distance of P from the plane 3x + 4y + 12z + 23 = 0 is (JEE Main 2022)
be P. Then the distance of P from the plane 3x + 4y + 12z + 23 = 0 is (JEE Main 2022)
(a) 5
(b) 50/13
(c) 4
(d) 63/13
Ans. a
Let P = (4t − 2, 2t + 1, 3t − 1)∵ P is the foot of perpendicular of (1, 2, 4)
∴ 4(4t − 3) + 2(2t − 1) + 3(3t − 5) = 0
⇒ 29t = 29 ⇒ t = 1
∴ P = (2, 3, 2)
Now, distance of P from the plane
3x + 4y + 12z + 23 = 0, is
Q.76. Let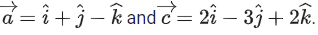 Then the number of vectors
Then the number of vectors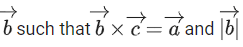 ∈ {1, 2, ........, 10} is: (JEE Main 2022)
∈ {1, 2, ........, 10} is: (JEE Main 2022)
(a) 0
(b) 1
(c) 2
(d) 3
Ans. a
= 2 − 3 − 2 = 0⇒ −3 = 0 (Not possible)
⇒ No possible value of
is possible.
Q.77. Let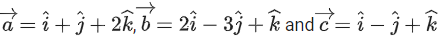 be three given vectors. Let
be three given vectors. Let 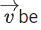 a vector in the plane of
a vector in the plane of whose projection on
whose projection on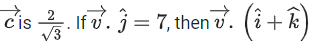 is equal to: (JEE Main 2022)
is equal to: (JEE Main 2022)
(a) 6
(b) 7
(c) 8
(d) 9
Ans. d
from equation (i) and (ii)
Q.78. If the lines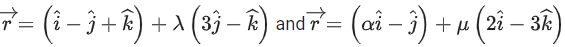 are co-planar, then the distance of the plane containing these two lines from the point (α, 0, 0) is: (JEE Main 2022)
are co-planar, then the distance of the plane containing these two lines from the point (α, 0, 0) is: (JEE Main 2022)
(a) 2/9
(b) 2/11
(c) 4/11
(d) 2
Ans. b
∵ Both lines are coplanar, so
⇒ α = 5/3
Equation of plane containing both lines
⇒ 9x + 2y + 6z = 13
So, distance of (5/3, 0, 0) from this plane
Q.79. If the plane 2x + y − 5z = 0 is rotated about its line of intersection with the plane 3x − y + 4z − 7 = 0 by an angle of π/2, then the plane after the rotation passes through the point: (JEE Main 2022)
(a) (2, −2, 0)
(b) (−2, 2, 0)
(c) (1, 0, 2)
(d) (−1, 0, −2)
Ans. c
P1: 2x + y − 52 = 0, P2: 3x − y + 4z − 7 = 0Family of planes P1 and P2
P: P1 + λP2
∴ P: (2 + 3λ)x + (1 − λ)y + (−5 + 4λ)z − 7λ = 0
∵ P ⊥ P1
∴ 4 + 6λ + 1 − λ + 25 − 20λ = 0
λ = 2
∴ P: 8x − y + 32 − 14 = 0
It passes through the point (1, 0, 2)
Q.80. If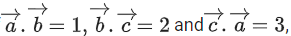 then the value of
then the value of 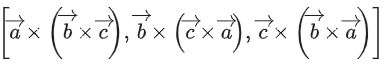 is: (JEE Main 2022)
is: (JEE Main 2022)
(a) 0
(b)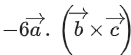
(c)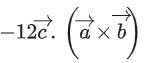
(d)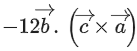
Ans. a
So, vectorsare coplanar, hence their Scalar triple product will be zero.
Q.81. Let the plane 2x + 3y + z + 20 = 0 be rotated through a right angle about its line of intersection with the plane x − 3y + 5z = 8. If the mirror image of the point (2,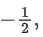 2) in the rotated plane is B(a, b, c), then: (JEE Main 2022)
2) in the rotated plane is B(a, b, c), then: (JEE Main 2022)
(a)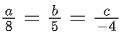
(b)
(c)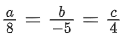
(d)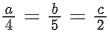
Ans. a
Consider the equation of plane,P: (2x + 3y + z + 20) + λ(x − 3y + 5z − 8) = 0
P: (2 + λ)x + 3(3 − 3λ)y + 1(1 + 5λ)z + (20 − 8λ) = 0
∵ Plane P is perpendicular to 2x + 3y + z + 20 = 0
So, 4 + 2λ + 9 − 9λ + 1 + 5λ = 0
⇒ λ = 7
P: 9x − 18y + 36z − 36 = 0
or P: x − 2y + 4z = 4
If image of (2,
2) in plane P is (a, b, c) then
So, a : b : c = 8 : 5 : −4
Q.82. If the two lines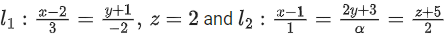 are perpendicular, then an angle between the lines
are perpendicular, then an angle between the lines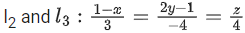 is: (JEE Main 2022)
is: (JEE Main 2022)
(a)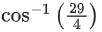
(b)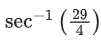
(c)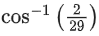
(d)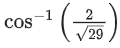
Ans. b
∵ L1 and L2 are perpendicular, so
⇒ α = 3
Now angle between l2 and l3,
Q.83. Let p be the plane passing through the intersection of the planes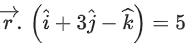 and
and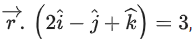 and the point (2, 1, −2). Let the position vectors of the points X and Y be
and the point (2, 1, −2). Let the position vectors of the points X and Y be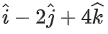 and
and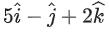 respectively. Then the points (JEE Main 2022)
respectively. Then the points (JEE Main 2022)
(a) X and X + Y are on the same side of P
(b) Y and Y − X are on the opposite sides of P
(c) X and Y are on the opposite sides of P
(d) X + Y and X − Y are on the same side of P
Ans. c
Let the equation of required planeπ: (x + 3y − z − 5) + λ(2x − y + z − 3) = 0
∵ (2, 1, −2) lies on it so, 2 + λ(−2) = 0
⇒ λ = 1
Hence, π: 3x + 2y − 8 = 0
∵ πx = −9, πy = 5, πx+y = 4
πx−y = −22 and πy−x = 6
Clearly X and Y are on opposite sides of plane π
Q.84. Let Q be the mirror image of the point P(1, 0, 1) with respect to the plane S : x + y + z = 5. If a line L passing through (1, −1, −1), parallel to the line PQ meets the plane S at R, then QR2 is equal to: (JEE Main 2022)
(a) 2
(b) 5
(c) 7
(d) 11
Ans. b
As L is parallel to PQ d.r.s of S is <1, 1, 1>
Point of intersection of L and S be λ⇒ (λ + 1) + (λ − 1) + (λ − 1) = S
⇒ λ = 2
∴ R ≡ (3, 1, 1)
Let Q(α, β, γ)
⇒ α = 3, β = 2, γ = 3
⇒ Q ≡ (3, 2, 3)
(QR)2 = 02 + (1)2 + (2)2 = 5
Q.85. Let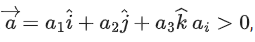 i = 1, 2, 3 be a vector which makes equal angles with the coordinate axes OX, OY and OZ. Also, let the projection of
i = 1, 2, 3 be a vector which makes equal angles with the coordinate axes OX, OY and OZ. Also, let the projection of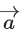 on the vector
on the vector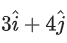 be 7. Let
be 7. Let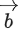 be a vector obtained by rotating
be a vector obtained by rotating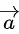 with 90∘. If
with 90∘. If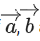 and x-axis are coplanar, then projection of a vector
and x-axis are coplanar, then projection of a vector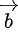 on
on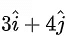 is equal to: (JEE Main 2022)
is equal to: (JEE Main 2022)
(a) √7
(b) √2
(c) 2
(d) 7
Ans. b
Q.86. Let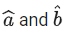 be two unit vectors such that
be two unit vectors such that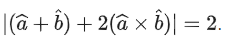 . If θ ∈ (0, π) is the angle between
. If θ ∈ (0, π) is the angle between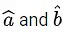 ,then among the statements:
,then among the statements: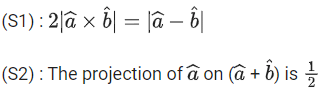 (JEE Main 2022)
(JEE Main 2022)
(a) Only (S1) is true.
(b) Only (S2) is true.
(c) Both (S1) and (S2) are true.
(d) Both (S1) and (S2) are false.
Ans. c
∴ cosθ = cos2θ∴ θ = 2π/3
where θ is angle between
.
(S1) is correct.
And projection of
(S2) is correct.
Q.87. Let the points on the plane P be equidistant from the points (−4, 2, 1) and (2, −2, 3). Then the acute angle between the plane P and the plane 2x + y + 3z = 1 is (JEE Main 2022)
(a) π/6
(b) π/4
(c) π/3
(d) 5π/12
Ans. c
Let P(x, y, z) be any point on plane P1Then (x + 4)2 + (y − 2)2 + (z − 1)2 = (x − 2)2 + (y + 2)2 + (z − 3)2
⇒ 12x − 8y + 4z + 4 = 0
⇒ 3x − 2y + z + 1 = 0
And P2: 2x + y + 3z = 0
∴ angle between P1 and P2
Q.88. If the shortest distance between the lines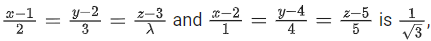 then the sum of all possible value of λ is: (JEE Main 2022)
then the sum of all possible value of λ is: (JEE Main 2022)
(a) 16
(b) 6
(c) 12
(d) 15
Ans. a
∴ Shortest distance
⇒ 3(5 − 2λ)2 = (15 − 4λ)2 + (10 − λ)2 + 25⇒ 5λ2 − 80λ + 275 = 0
∴ Sum of values of λ = 80/5 = 16
Q.89. Let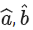 be unit vectors. If
be unit vectors. If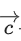 be a vector such that the angle between
be a vector such that the angle between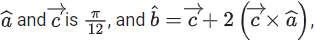 then
then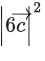 is equal to: (JEE Main 2022)
is equal to: (JEE Main 2022)
(a) 6(3 − √3)
(b) 3 + √3
(c) 6(3 + √3)
(d) 6(√3 + 1)
Ans. c