Short Notes: Transient Analysis in AC & DC Circuits | Network Theory (Electric Circuits) - Electrical Engineering (EE) PDF Download

Introduction

Many applications of control theory are to servomechanisms which are systems using the feedback principle designed so that the output will follow the input. Hence there is a need for studying the time response of the system. The time response of a system may be considered in two parts:

• Transient response: this part reduces to zero as t → ∞
• Steady-state response: response of the system as t → ∞

Clear all your Electrical Engineering (EE) doubts with EduRev Join for Free

Join for Free

Response of the first order systems

• Consider the output of a linear system in the form Y(s) = G(s)U(s) where Y(s): Laplace transform of the output, G(s): transfer function of the system and U(s): Laplace transform of the input.
• Consider the first-order system of the form ay + y = u, its transfer function is
  
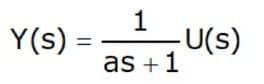
• For a transient response analysis, it is customary to use a reference unit step function u(t) for which
  U(s) = 1/s
• It then follows that
  
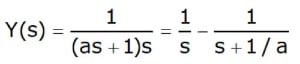
• On taking the inverse Laplace of the equation, we obtain
  
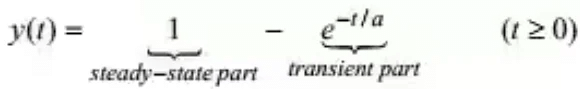
• The response has an exponential form. The constant 'a' is called the time constant of the system.
  
• Notice that when t = a, then y(t)= y(a)= 1- e^-1=0.63. The response is in two parts, the transient part e-t/a, which approaches zero as t →∞ and the steady-state part 1, which is the output when t → ∞.
• If the derivative of the input are involved in the differential equation of the system, that is if
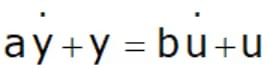  then its transfer function is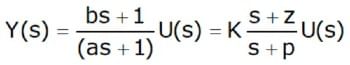
• where
  K = b / a
  z =1/ b: the zero of the system
  p =1/ a: the pole of the system
• When U(s) =1/ s, Equation can be written as
  
  
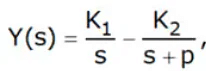
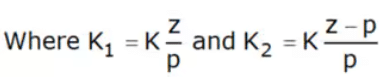
• Hence,
  
• With the assumption that z>p>0, this response is shown in
  
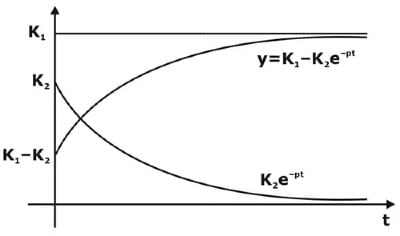
• We note that the responses to the systems have the same form, except for the constant terms K₁ and K₂ . It appears that the role of the numerator of the transfer function is to determine these constants, that is, the size of y(t), but its form is determined by the denominator.

Response of second-order systems 

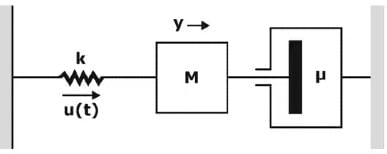
• An example of a second-order system is a spring-dash pot arrangement, Applying Newton’s law, we find
  
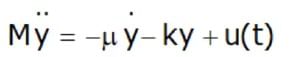
• where k is spring constant, µ is damping coefficient, y is the distance of the system from its position of the equilibrium point, and it is assumed that y(0) = y(0)' = 0.
  
• Hence,
  
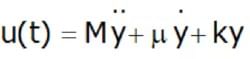
• On taking Laplace transforms, we obtain,
  
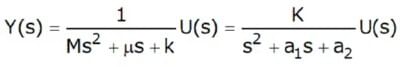
• where K =1/ M , a1 = µ / M , a2 = k / M . Applying a unit step input, we obtain
  
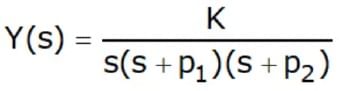
• where
  
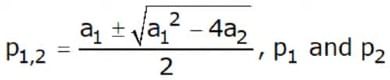
  are the poles of the transfer function
  
  that is, the zeros of the denominator of G(s).
• There are there cases to be considered:
  (i) over-damped system:
  In this case, p₁ and p₂ are both real and unequal. The equation can be written as
  
  
  
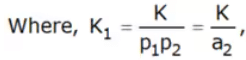
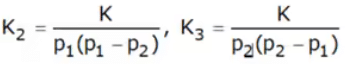
  (ii) critically damped system
  In this case, the poles are equal: p₁ = p₂ = a₁ / 2 = p , and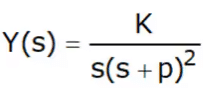
  
  
  
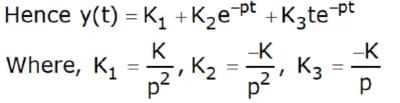
  (iii) under-damped system
  In this case, the poles p₁ and p₂ are complex conjugate having the form
  
  
  

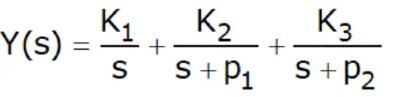
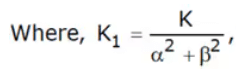
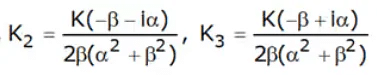
The three cases discussed above are plotted as: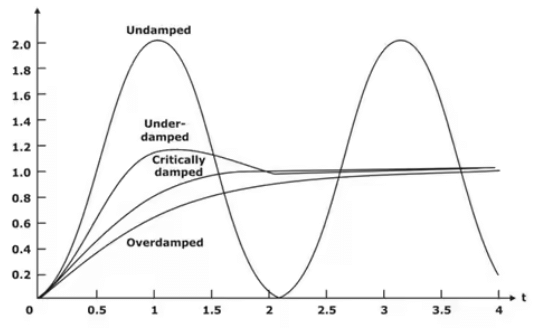

There are two important constants associated with each second order system:

• The undamped natural frequency ωn of the system is the frequency of the response shown in Fig.
  
• The damping ratio ξ of the system is the ratio of the actual damping µ(= a1M) to the value of the damping µc , which results in the system being critically damped.
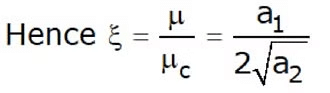
• also
  
  

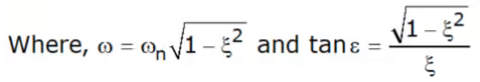
Some definitions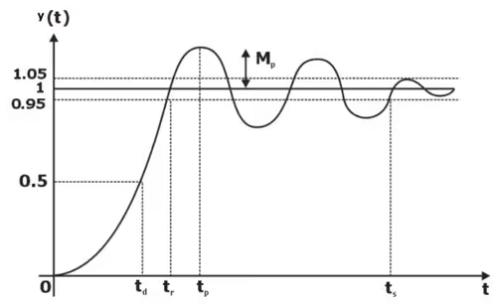

Overshoot: defined as 

• Time delay τd: the time required for a system response to reach 50% of its final value
• Rise time: the time required for the system response to rising from 10% to 90% of its final value
• Settling time: the time required for the eventual settling down of the system response to be within (normally) 5% of its final value
• Steady-state error e_ss: the difference between the steady-state response and the input.

Download the notes Short Notes: Transient Analysis in AC & DC Circuits

Download as PDF

Download as PDF

Steady state error

Consider a unity feedback system

• where
  r(t) : reference input
  c(t) : system output
  e(t) : error
• We define the error function as
  e(t) = r(t) − c(t)
• hence,
  
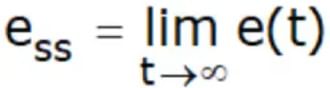
• Since E(s) = R(s) − A(s)E(s) , it follows that
  
  
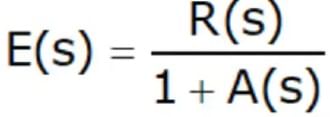
• and by the final value theorem
  
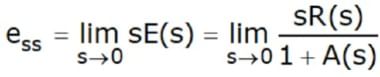
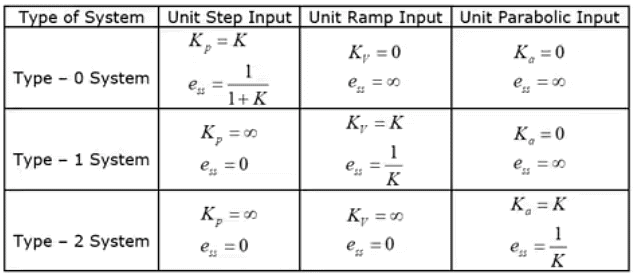
• We now define three error coefficients that indicate the steady-state error when the system is subjected to three different standard reference inputs r(s).
  step input:  r(t) = ku(t)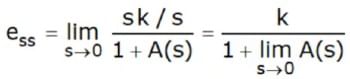
  
  
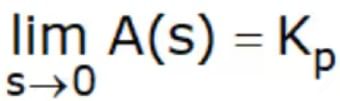
  called the position error constant, then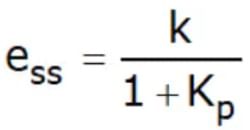
  

Ramp input: r(t) = ktu(t)
In this case,


 is called the velocity error constant.
Parabolic input: r(t) = 1/2 kt² u(t)
In this case,


is called the acceleration error constant.

• From the definition of the error coefficients, it is seen that e_ss depends on the number of poles at s = 0 of the transfer function. This leads to the following classification. A transfer function is said to be of type N if it has N poles at the origin. Thus if
  
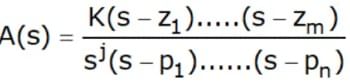
• At s = 0,
   
  
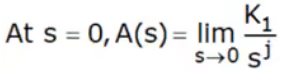
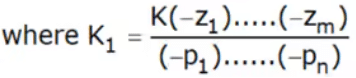
   K₁ is called the gain of the transfer function.
• Hence the steady-state error e_ss is summarized in Table