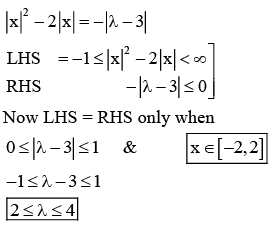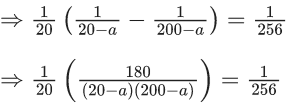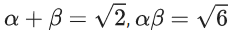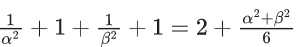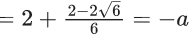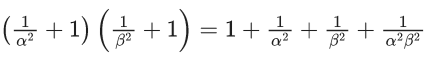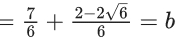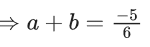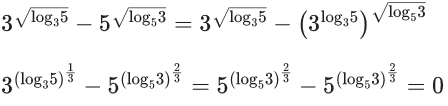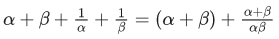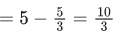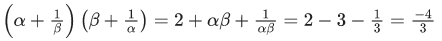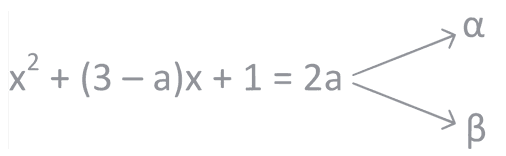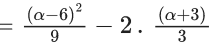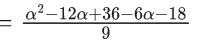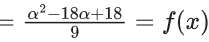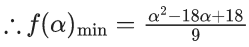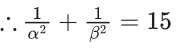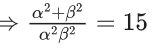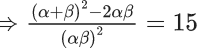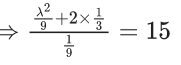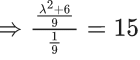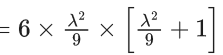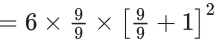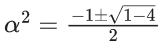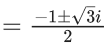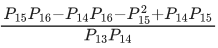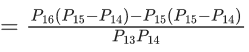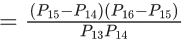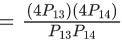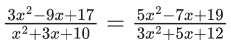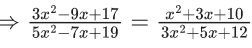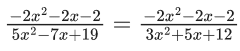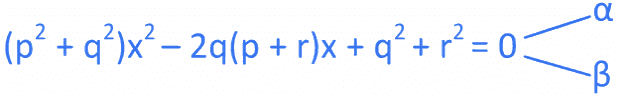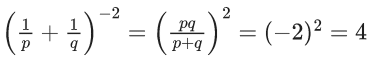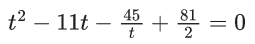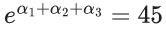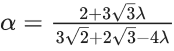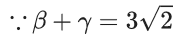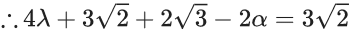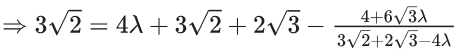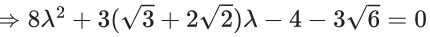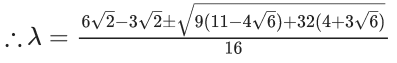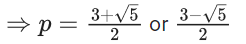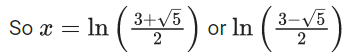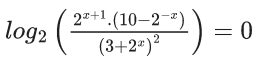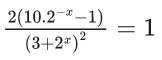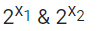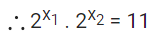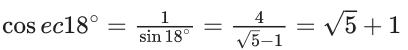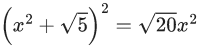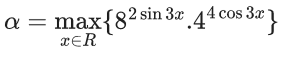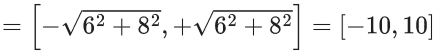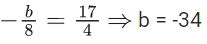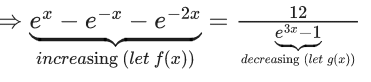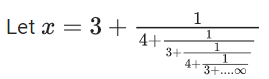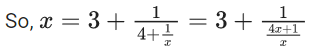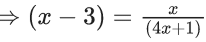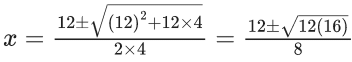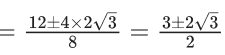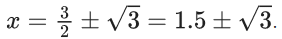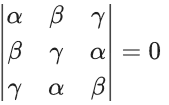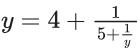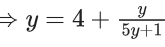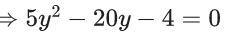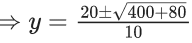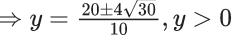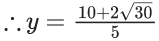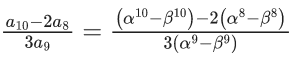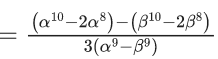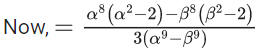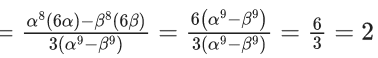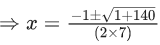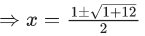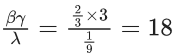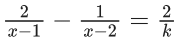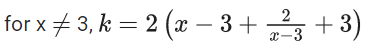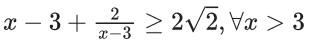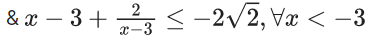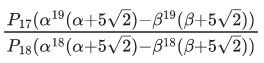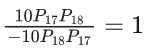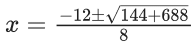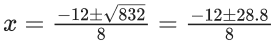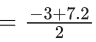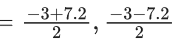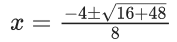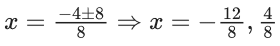JEE Main Previous year questions (2021-23): Quadratic Equation and Inequations (Inequalities) PDF Download

Q.1. The equation x² − 4x + [x] + 3 = x[x], where [x] denotes the greatest integer function, has :     (JEE Main 2023)
(a) a unique solution in (−∞, 1)
(b) no solution
(c) exactly two solutions in (−∞, ∞)
(d) a unique solution in (−∞, ∞)

Ans. d

x² – 4x + [x] + 3 = x [x]
x² – 4x + 3 = (x – 1) [x]
(x – 1) (x – 3) = (x – 1) [x]

x – [x] = 3
{x} = 3

Q.2. Let λ ∈ ℝ and let the equation E be |x|² − 2|x| + |λ − 3| = 0. Then the largest element in the set S = {x + λ: x is an integer solution of E} is      (JEE Main 2023)

Ans. 5
|x| - 2| x| + |λ - 3| = 0

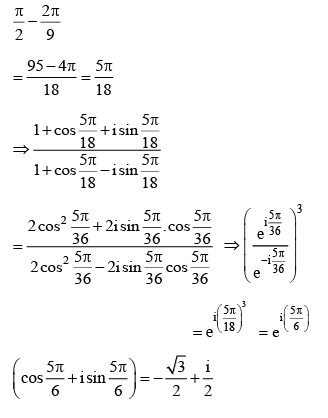
Q.3. The value of 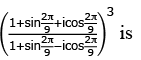       (JEE Main 2023)
(a)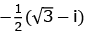
(b)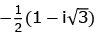
(c)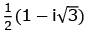
(d)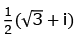

Ans. a

Q.4. The product of all positive real values of x satisfying the equation 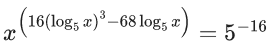 is ______.      (JEE Advanced 2022)

Ans. 1
Taking log to the base 5 on both sides
(16(log₅⁡x)³ − 68(log₅⁡x))(log₅⁡x) = −16
Let (log₅⁡x) = t
16t⁴ − 68t² + 16 = 0
⇒ 4t⁴ − 16t²− t² + 4 = 0
⇒ (4t²−1)(t²−4) = 0
⇒ t = ±(1/2), ± 2
So log₅⁡x = ±(1/2) or ±2
⇒ x = 5^1/2, 5^(−1/2), 5², 5⁻²

Q.5. If 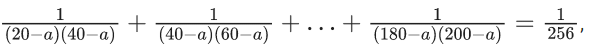 then the maximum value of a is :      (JEE Main 2022)
(a) 198
(b) 202
(c) 212
(d) 218

Ans. c


⇒ (20−a)(200−a) = 9.256
OR a² − 220a + 1696 = 0
⇒ a = 212, 8

Q.6. Let α, β be the roots of the equation x² − √2x + √6 = 0 and 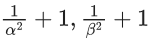 be the roots of the equation x² + ax + b = 0. Then the roots of the equation x² − (a + b − 2)x + (a + b + 2) = 0 are :     (JEE Main 2022)
(a) non-real complex numbers
(b) real and both negative
(c) real and both positive
(d) real and exactly one of them is positive

Ans. b






So, equation is
OR 6x² + 17x + 7 = 0
Both roots of equation are −ve and distinct

Q.7. If α, β are the roots of the equation 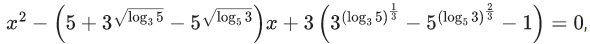  then the equation, whose roots are (α + (1/β)) and (β + (1/α)), is :       (JEE Main 2022)
(a) 3x² − 20x − 12 = 0
(b) 3x² − 10x − 4 = 0
(c) 3x² − 10x + 2 = 0
(d) 3x² − 20x + 16 = 0

Ans. b

Note : In the given equation 'x' is missing.
So,




So Equation must be option (b).

Q.8. The minimum value of the sum of the squares of the roots of x² + (3 − a)x + 1 = 2a is:      (JEE Main 2022)
(a) 4
(b) 5
(c) 6
(d) 8

Ans. c

α + β = a−3, αβ = 1−2a
⇒ α² + β² = (a−3)² −2(1 − 2a)
= a² − 6a + 9 − 2 + 4a
= a² − 2a + 7
= (a−1)² + 6
So, α² + β² ≥ 6

Q.9. Let S be the set of all integral values of α for which the sum of squares of two real roots of the quadratic equation 3x² + (α − 6)x + (α + 3) = 0 is minimum. Then S :      (JEE Main 2022)
(a) is an empty set
(b) is a singleton
(c) contains exactly two elements
(d) contains more than two elements

Ans. a
Given quadratic equation,
3x²  +(α−6)x + (α+3) = 0
Let, a and b are the roots of the equation,
∴ a + b = −(α−6)/3
and ab = (α+3)/3
For real roots,
D ≥ 0
⇒ (α−6)² − 4.3.(α + 9) ≥ 0
⇒ α²−12α + 36 − 12α − 36 ≥ 0
⇒ α² − 24 α ≥ 0
⇒ α(α−24)≥0
∴ α > 24 or α<0

∴ Real roots of the equation possible for α>24 or α<0.
Now, sum of square of roots
= a² + b²
= (a + b)² - 2ab



∴ Sum of square of roots are minimum when a² + b² = minimum.

Value of quadratic equation α² − 18α + 18 is minimum at

But for real roots α should be less than 0 or greater than 24.
So, there is no value of α in the range α > 24 ∪ α < 0 where sum of squares of two real roots is minimum.
∴ S is an empty set.

Q.10. If the sum of the squares of the reciprocals of the roots α and β of the equation 3x² + λx − 1 = 0 is 15, then 6(α³ + β³)² is equal to :      (JEE Main 2022)
(a) 18
(b) 24
(c) 36
(d) 96

Ans. b
3x² + λx − 1 = 0
Given, two roots are α and β.
∴ Sum of roots = α + β = ((−λ)/3)
And product of roots = αβ = ((−1)/3)
Given that,
Sum of square of reciprocal of roots α and β is 15.





⇒ λ² + 6 = 15
⇒ λ² = 9
Now, 6(α³ + β³)²
= 6{(α + β)(α² + β² − αβ)}²



= 6 x (2)²
= 6 x 4 = 24

Q.11. The number of distinct real roots of the equation x⁷ − 7x − 2 = 0 is     (JEE Main 2022)
(a) 5
(b) 7
(c) 1
(d) 3

Ans. d
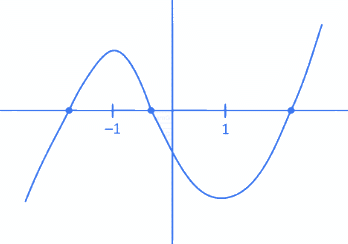
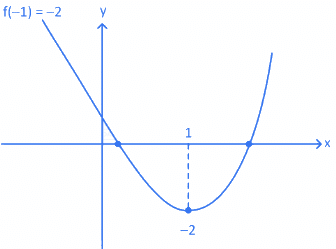
Given equation x⁷ − 7x − 2 = 0
Let f(x) = x⁷ − 7x − 2
f′(x) = 7x⁶ − 7 = 7(x⁶ − 1)
and f′(x) = 0 ⇒ x = +1
and f(−1) = −1 + 7 − 2 = 5 > 0
f(1) = 1 − 7 − 2 = −8 < 0
So, roughly sketch of f(x) will be

So, number of real roots of f(x) = 0 and 3

Q.12. The sum of all the real roots of the equation (e^2x − 4)(6e^2x − 5e^x + 1) = 0 is     (JEE Main 2022)
(a) log_e3
(b) -log_e3
(c)log_e6
(d) -log_e6

Ans. b
(e^2x − 4)(6e^2x − 5e^x + 1) = 0
Let e^x = t
∴ (t² − 4)(6t² − 5t + 1) = 0
⇒(t² − 4)(2t − 1)(3t − 1) = 0
∴ t = 2, −2, (1/2), (1/3)
∴ e^x = 2 ⇒ x = ln⁡2
e^x = −2 (not possible)
e^x = (1/2) ⇒ x = −ln⁡2
e^x = (1/3) ⇒ x = −ln⁡3
∴ Sum of all real roots
= ln⁡2 − ln⁡2 − ln⁡3
= − ln⁡3

Q.13. Let a, b ∈ R be such that the equation ax² − 2bx + 15 = 0 has a repeated root α. If α and β are the roots of the equation x² − 2bx + 21 = 0, then α² + β² is equal to :     (JEE Main 2022)
(a) 37
(b) 58
(c) 68
(d) 92

Ans. b
ax² − 2bx + 15 = 0 has repeated root so b² = 15a and α = 15b
∵ α is a root of x² − 2bx + 21 = 0
So 225/(b²) = 9 ⇒ b² = 25
Now α² + β² = (α + β)² − 2αβ = 4b² − 42 = 100 − 42 = 58

Q.14. The number of distinct real roots of x⁴ − 4x + 1 = 0 is :      (JEE Main 2022)
(a) 4
(b) 2
(c) 1
(d) 0

Ans. b
f(x) = x⁴ - 4x + 1 = 0
f'(x) = 4x³ - 4
= 4(x - 1)(x² + 1 + x)

⇒ Two solution

Q.15. The number of real solutions of x⁷ + 5x³ + 3x + 1 = 0 is equal to _____.     (JEE Main 2022)
(a) 0
(b) 1
(c) 3
(d) 5

Ans. b

Q.16. Let f(x) be a quadratic polynomial such that f(−2) + f(3) = 0. If one of the roots of f(x) = 0 is −1, then the sum of the roots of f(x) = 0 is equal to :      (JEE Main 2022)
(a) 11/3
(b) 7/3
(c) 13/3
(d) 14/3

Ans. a
∵ x = −1 be the roots of f(x) = 0
∴ Let f(x) = A(x + 1)(x − 1) ...... (i)
Now, f(−2) + f(3) = 0
⇒ A[−1(−2 − b) + 4(3 − b)] = 0
b = (14/3)
∴ Second root of f(x) = 0 will be 14/3
∴ Sum of roots =(14/3) − 1 = (11/3)

Q.17. Let α be a root of the equation 1 + x² + x⁴ = 0. Then, the value of α¹⁰¹¹ + α²⁰²² − α³⁰³³ is equal to :     (JEE Main 2022)
(a) 1
(b) α
(c) 1 + α
(d) 1 + 2α

Ans. a
Given, α is a root of the equation 1 + x² + x⁴ = 0
∴ α will satisfy the equation.
∴ 1 + α² + α⁴ = 0


∴ α² = ωarω²
Now,
α¹⁰¹¹ + α²⁰²² − α³⁰³³
= α.(α²)⁵⁰⁵ + (α²)¹⁰¹¹ − α.(α²)¹⁵¹⁶
= α(ω)⁵⁰⁵ + (ω)¹⁰¹¹ − α.(ω)¹⁵¹⁶
= α.(ω³)¹⁶⁸.ω + (ω³)³³⁷ − α.(ω³)⁵⁰⁵.ω
= αω + 1 − αω
= 1

Q.18. Let α, β(α > β) be the roots of the quadratic equation x² − x − 4 = 0. If P_n = αⁿ − βⁿ, n ∈ N, then 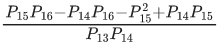 is equal to _____.     (JEE Main 2022)

Ans. 16
α and β are the roots of the quadratic equation x² − x − 4 = 0.
∴ α and β are satisfy the given equation.
α² − α − 4 = 0
⇒ α^{n + 1} − αⁿ − 4α^{n − 1} = 0 ...... (1)
and β² − β − 4 = 0
⇒ βⁿ⁺¹ − βⁿ − 4βⁿ⁻¹ = 0 ...... (2)
Substituting (2) from (1), we get,
(αⁿ⁺¹ − βⁿ⁺¹)−(αⁿ − βⁿ)−4(α^{n − 1} − β^{n − 1}) = 0
⇒ P_{n +1} − P_n − 4P_n−1 = 0
⇒ P_n+1 = P_n + 4P_n−1
⇒ P_n+1 − P_n = 4P_n−1
For n = 14, P₁₅ − P₁₄ = 4P₁₃
For n = 15, P₁₆ − P₁₅ = 4P₁₄
Now,



= 16

Q.19. The sum of all real values of x for which  is equal to _____.     (JEE Main 2022)

Ans. 6



Either x² + x + 1 = 0 or No real roots
⇒ 5x² − 7x + 19 = 3x² + 5x + 12
2x² − 12x + 7 = 0
sum of roots = 6.

Q.20. The number of distinct real roots of the equation x⁵(x³ − x ² − x + 1) + x(3x³ − 4x² − 2x + 4) − 1 = 0 is _______.     (JEE Main 2022)

Ans. 3
x⁸ − x⁷ − x⁶ + x⁵ + 3x⁴ − 4x³ − 2x² + 4x − 1 = 0
⇒ x⁷(x − 1) − x⁵(x − 1) + 3x³(x − 1) − x(x² − 1) + 2x(1 − x) + (x − 1) = 0
⇒ (x − 1)(x⁷ − x⁵ + 3x³−x(x + 1)−2x + 1)= 0
⇒ (x − 1)(x⁷ − x⁵ + 3x³ − x² − 3x + 1) = 0
⇒ (x − 1)(x⁵(x² − 1) + 3x(x²−1)−1(x²−1)) = 0
⇒ (x − 1)(x² − 1)(x⁵ + 3x − 1) = 0
∴ x = ±1 are roots of above equation and x⁵ + 3x − 1 is a monotonic term hence vanishs at exactly one value of x other than 1 or −1.
∴ 3 real roots.

Q.21. If for some 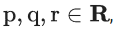 not all have same sign, one of the roots of the equation (p² + q²)x² − 2q(p + r)x + q² + r² = 0 is also a root of the equation x² + 2x − 8 = 0, then (q² + r²)/p² is equal to ____________,      (JEE Main 2022)

Ans. 272
Let roots of

∴ α + β > 0 and αβ > 0
Also, it has a common root with x² + 2x − 8 = 0
∴ The common root between above two equations is 4.
⇒ 16(p² + q²)−8q(p + r)+ q² + r² = 0
⇒ (16p² − 8pq + q²) + (16q² − 8qr + r²) = 0
⇒ (4p − q)²+ (4q − r)² = 0
⇒ q = 4p and r = 16p

∴  

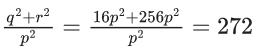
Q.22. Let for f(x) = a₀x² + a₁x + a₂,f′(0) = 1 and f′(1) = 0. If a₀, a₁, a₂ are in an arithmatico-geometric progression, whose corresponding A.P. has common difference 1 and corresponding G.P. has common ratio 2, then f(4) is equal to _____.       (JEE Main 2022)

Ans. 2
Given,
f(x) = a₀x² + a₁x + a₂
f′(0) = 1
f′(1) = 0
a₀, a₁, a₂ are in A. G. P
Common difference of AP = 1
Common ratio of GP = 2
A.P terms = a, a + 1, a + 2
G.P terms = y, ry, r²y
∴ AGP terms = ay, (a + 1)ry, (a + 2)r²y
∴ a₀ = ay
a₁ = (a + 1)ry = (a + 1)2y
a₂ = (a + 2)r²y = (a + 2)4y
Now, f′(x) = 2xa₀ + a₁
∴ f′(0) = a₁ = 1
and f′(1) = 2a₀ + a₁ = 0
⇒ 2a₀ + 1 = 0
⇒ a₀ = −12
∴ ay = −(1/2)
and (a + 1)2y = 1
⇒ 2ay + 2y = 1
⇒ 2 × (−(1/2))+2y=1
⇒ 2y = +2
⇒ y =  +1
∴ a = −(1/2)
∴ a₂ = (a + 2)4y
= (−(1/2) + 2) × 4.1
= 6
∴ f(x) = −(1/2)x² + x + 6
∴ f(4) = −(1/2)(4)² + 4 + 6
= − 8 + 10
= 2

Q.23. Let p and q be two real numbers such that p + q = 3 and p⁴ + q⁴ = 369. Then ((1/p) + (1/q))⁻² is equal to ______.     (JEE Main 2022)

Ans. 4
∵ p + q = 3 ...... (i)
and p⁴ + q⁴ = 369 ...... (ii)
{(p+q)² − 2pq}² − 2p²q² = 369
or (9 − 2pq)² − 2(pq)² = 369
or (pq)² − 18pq − 144 = 0
∴ pq = −6 or 24
But pq = 24 is not possible
∴ pq = −6
Hence,

Q.24. The sum of the cubes of all the roots of the equation x⁴ − 3x³ − 2x² + 3x + 1 = 0 is _______.      (JEE Main 2022)

Ans. 36
x⁴ − 3x³ − x² − x² + 3x + 1 = 0
(x² − 1)(x² − 3x − 1) = 0
Let the root of x² − 3x − 1 = 0 be α and β and other two roots of given equation are 1 and −1
So sum of cubes of roots
= 1³ + (−1)³ + α³ + β³
= (α+β)³ − 3αβ(α + β)
= (3)³ − 3(−1)(3)
= 36

Q.25. If the sum of all the roots of the equation e^2x − 11e^x− 45e^−x+ (81/2) = 0 is log_ep, then p is equal to ______.       (JEE Main 2022)

Ans. 45
Let e^x = t then equation reduces to

⇒ 2t³ − 22t² + 81t − 45 = 0 ..... (i)
if roots of e^2x − 11e^x − 45e^−x + (81/2) = 0 are α, β, γ then roots of (i) will be  using product of roots
⇒ α₁ + α₂ + α₃ = ln⁡ 45 ⇒ p = 45

Q.26. Let α, β be the roots of the equation x² − 4λx + 5 = 0 and α, γ be the roots of the equation x² − (3√2 + 2√3)x + 7 + 3λ√3 = 0, λ > 0. If β + γ = 3√2, then (α + 2β + γ)² is equal to ____.      (JEE Main 2022)

Ans. 98
∵ α, β are roots of x² − 4λx + 5 = 0
∴ α + β = 4λ and αβ = 5
Also, α, γ are roots of
x² − (3√2 + 2√3)x + 7 + 3√3λ = 0, λ > 0
∴ α + γ = 3√2 + 2√3, αγ = 7 + 3√3λ
∵ α is common root
∴ α² − 4λα + 5 = 0 ....... (i)
and α² − (3√2 + 2√3)α + 7 + 3√3λ = 0 ...... (ii)
From (i) - (ii) : we get





∴ λ = 2
∴ (α + 2β + γ)² = (α + β + β + γ)²
= (4√2 + 3√2)²
= (7√2)² = 98

Q.27. The number of real solutions of the equation e^4x + 4e^3x − 58e^2x + 4e^x + 1 = 0 is _____.     (JEE Main 2022)

Ans. 2
Dividing by e2x
e^2x + 4e^x − 58 + 4e^−x + e^−2x = 0
⇒(e^x + e^−x)² + 4(e^x + e^−x) − 60 = 0
Let e^x + e^−x = t ∈ [2, ∞)
⇒ t² + 4t − 60 = 0
⇒ t = 6 is only possible solution
e^x + e^−x = 6 ⇒ e^2x − 6e^x + 1 = 0
Let e^x = p,
p² − 6p + 1 = 0

Q.28. The numbers of pairs (a, b) of real numbers, such that whenever α is a root of the equation x² + ax + b = 0, α² − 2 is also a root of this equation, is :     (JEE Main 2021)
(a) 6
(b) 2
(c) 4
(d) 8

Ans. a
Consider the equation x² + ax + b = 0
If has two roots (not necessarily real α & β)
Either α = β or α ≠ β
Case (1) If α = β, then it is repeated root. Given that α² − 2 is also a root
So, α = α² − 2 ⇒ (α + 1)(α − 2) = 0
⇒ α = −1 or α = 2
When α = −1 then (a, b) = (2, 1)
α = 2 then (a, b) = (−4, 4)
Case (2) If α ≠ β
Then
(I) α = α² − 2 and β = β² − 2
Hence, (a, b) = (−(α + β), αβ)
(−1, −2)
(II) α = β² − 2 and β = α² − 2
Then α − β = β² − α² = (β − α) (β + α)
Since α ≠ β we get α + β = β² + α² − 4
α + β = (α + β)² − 2αβ − 4
Thus −1 = 1 −2 αβ − 4 which implies
αβ = −1 Therefore (a, b) = (−(α + β), αβ)
= (1, −1)
(III) α = α² − 2 = β² − 2 and α ≠ β
⇒ α = − β
Thus α = 2, β = −2
α = −1, β = 1
Therefore (a, b) = (0, −4) & (0, 1)
(IV) β = α² − 2 = β² − 2 and α ≠ β is same as (III) Therefore we get 6 pairs of (a, b)
Which are (2, 1), (−4, 4), (−1, −2), (1, −1), (0, −4)
Option (a)

Q.29. The sum of the roots of the equation x + 1 − 2log₂(3 + 2^x) + 2log₄(10 − 2^−x) = 0, is :
(a) log₂ 14
(b) log₂ 11
(c) log₂ 12
(d) log₂ 13

Ans. b
x + 1 − 2log₂(3 + 2^x) + 2log₄(10 − 2^−x) = 0
log₂(2^x+1 )− log₂(3+2^x)² + log₂(10 − 2^−x) = 0


⇒ 20.2^x − 2 = 9 + 2^2x + 6.2^x
∴ (2^x)² − 14(2^x) + 11 = 0
Roots are

x₁ + x₂ = log₂(11)

Q.30. cosec18∘ is a root of the equation :     (JEE Main 2021)
(a) x² + 2x − 4 = 0
(b) 4x² + 2x − 1 = 0
(c) x² − 2x + 4 = 0
(d) x² − 2x − 4 = 0

Ans. d

Let cos⁡ec18^∘ = x = √5 + 1
⇒ x−1 = √5
Squaring both sides, we get
x² − 2x + 1 = 5
⇒ x² - 2x - 4 = 0

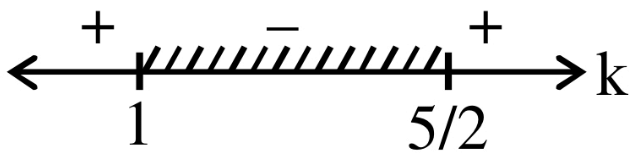
Q.31. The set of all values of K > −1, for which the equation (3x² + 4x + 3)² − (k + 1)(3x² + 4x + 3)(3x² + 4x + 2) + k(3x² + 4x + 2)² = 0 has real roots, is :     (JEE Main 2021)
(a) (1, (5/2)]
(b) [2, 3)
(c) [-(1/2), (1)
(d)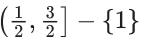

Ans. a
(3x2 + 4x + 3)² − (k + 1)(3x² + 4x + 3)(3x² + 4x + 2) + k(3x² + 4x + 2)2 = 0
Let 3x² + 4x + 3 = a
and 3x² + 4x+ 2= b ⇒ b = a − 1
Given equation becomes
⇒ a2 − (k + 1)ab + kb² = 0
⇒ a(a − kb) − b(a − kb) = 0
⇒ (a − kb)(a − b) = 0 ⇒ a = kb or a = b (reject) ∵ a = kb
⇒ 3x² + 4x + 3 = k(3x² + 4x + 2)
⇒ 3(k − 1)x² + 4(k − 1)x + (2k − 3) = 0 for real roots
D ≥ 0
⇒ 16(k − 1)² − 4(3(k − 1))(2k − 3) ≥ 0
⇒ 4(k − 1){4(k − 1) − 3(2k − 3)} ≥ 0
⇒ 4(k− 1){−2k + 5} ≥ 0
⇒ −4(k − 1){2k − 5} ≥ 0
⇒ (k − 1)(2k − 5) ≤ 0

∴ k ∈ [1, (5/2)]
∴ k ≠ 1
∴ k ∈ (1, (5/2))

Q.32. Let α, β be two roots of the equation x² + (20)^1/4x + (5)^1/2 = 0. Then α⁸ + β⁸ is equal to      (JEE Main 2021)
(a) 10
(b) 100
(c) 50
(d) 160

Ans. c
x² + (20)^1/4x + (5)^1/2 = 0
⇒ x² + √5 = - (20)^1/4x
Squaring both sides, we get

⇒ x⁴ = −5 ⇒ x⁸ = 25
⇒ α⁸ + β⁸ = 50

Q.33. The number of real solutions of the equation, x² − |x| − 12 = 0 is :     (JEE Main 2021)
(a) 2
(b) 3
(c) 1
(d) 4

Ans. a
|x|² − |x| − 12 = 0
⇒ (|x| + 3)(|x| − 4) = 0
⇒ |x| = 4
⇒ x = ±2

Q.34. Let 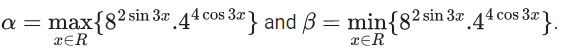 If 8x² + bx + c = 0 is a quadratic equation whose roots are α^1/5 and β^1/5, then the value of c − b is equal to :      (JEE Main 2021)
(a) 42
(b) 47
(c) 43
(d) 50

Ans. a

= max{2^6sin⁡3x.2^8cos⁡3x}
= max{2^{6sin⁡3x+8cos⁡3x}}
and β = min{8^2sin⁡3x.4^4cos⁡3x} = min{2^{6sin⁡3x + 8cos⁡3x}}
Now range of 6sin3x + 8cos3x

α = 2¹⁰ & β = 2⁻¹⁰
So, α^1/5 = 2² = 4
⇒ β^1/5 = 2⁻² = 1/4
quadratic 8x² + bx + c = 0

c/8 = 1 ⇒ c = 8
∴ c – b = 8 + 34 = 42

Q.35. The number of real roots of the equation e^6x − e^4x − 2e^3x − 12e^2x + e^x + 1 = 0 is :      (JEE Main 2021)
(a) 2
(b) 4
(c) 6
(d) 1

Ans. a
e^6x − e^4x−2e^3x−12e^2x + e^x + 1 = 0
⇒ (e^3x − 1)² − e^x(e^3x − 1) = 12e^2x
(e^3x − 1)²(e^x − e^−x − e^−2x) = 12


⇒ No. of real roots = 2

Q.36. If α and β are the distinct roots of the equation x² + (3)^1/4x + 3^1/2 = 0, then the value of α⁹⁶(α¹²−1) + β⁹⁶(β¹²−1) is equal to :      (JEE Main 2021)
(a) 56 x 3²⁵
(b) 56 x 3²⁴
(c) 52 x 3²⁴
(d) 28 x 3²⁵

Ans. c
As, (α² + √3)=−(3)^1/4.α
⇒ (α⁴ +2√3α² + 3) = √3α² (On squaring)
∴ (α⁴ + 3) = (−)√3α²
⇒ α⁸ + 6α⁴ + 9 = 3α⁴ (Again squaring)
∴ α⁸ + 3α⁴ + 9 = 0
⇒ α⁸ = −9 − 3α⁴
(Multiply by α4)
So, α¹² = −9α⁴ − 3α⁸
∴ α¹² = −9α⁴ − 3(−9−3α⁴)
⇒ α¹² = −9α⁴ + 27 + 9α⁴
Hence, α¹² = (27)²
⇒ (α¹²)⁸ = (27)⁸
⇒ α⁹⁶ = (3)²⁴
Similarly β⁹⁶ = (3)²⁴
∴ α⁹⁶(α¹²−1) + β⁹⁶(β¹²−1) = (3)²⁴ × 52
⇒ Option (3) is correct.

Q.37. The value of  is equal to     (JEE Main 2021)
(a) 1.5 + √3
(b) 2  + √3
(c) 3 + 2√3
(d) 4 + √3

Ans. a



⇒ (4x+1)(x−3)=x
⇒ 4x² −12x + x − 3 = x
⇒ 4x² −12x − 3 = 0



But only positive value is accepted
So, x = 1.5  + √3

Q.38. Let α, β, γ be the real roots of the equation, x³ + ax² + bx + c = 0, (a, b, c ∈ R and a, b ≠ 0). If the system of equations (in u, v, w) given by αu + βv + γw = 0, βu + γv + αw = 0; γu + αv + βw = 0 has non-trivial solution, then the value of a²/b is     (JEE Main 2021)
(a) 5
(b) 3
(c) 1
(d) 0

Ans. b
x³ + ax² + bx + c = 0
Roots are α, β, γ.
For non-trivial solutions,

⇒ α³ + β³ + γ³ − 3αβγ = 0
⇒ (α + β + γ)[(α + β + α)² − 3(∑αβ)] = 0
⇒ (−a)[a² − 3b] = 0
⇒ a² = 3b (∵ a ≠ 0)
⇒ a²/b = 3

Q.39. The value of 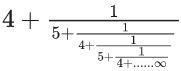 is:       (JEE Main 2021)
(a)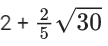
(b)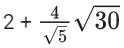
(c)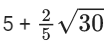
(d)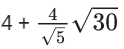

Ans. a

Q.40. Let α and β be the roots of x² − 6x − 2 = 0. If a_n = αⁿ − βⁿ for n ≥ 1, then the value of 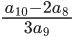 is :     (JEE Main 2021)
(a) 3
(b) 2
(c) 4
(d) 1

Ans. b
Given, α and β be the roots of x² − 6x − 2 = 0
α + β = 6
αβ = −2
and α² − 6α − 2 = 0 ⇒ α² − 2 = 6α
β² − 6β − 2 = 0 ⇒ β² − 2 = 6β

Q.41. The integer 'k', for which the inequality x² − 2(3k − 1)x + 8k² − 7 > 0 is valid for every x in R, is :     (JEE Main 2021)
(a) 4
(b) 2
(c) 3
(d) 0

Ans. c
x² − 2(3k−1)x + 8k² − 7 > 0
Now, D < 0
⇒ 4(3k−1)² − 4 × 1 × (8k² − 7) < 0
⇒ 9k² − 6k + 1 − 8k² + 7 < 0
⇒ k² − 6k + 8 < 0
⇒ (k−4)(k−2) < 0
2 < k < 4
then k = 3

Q.42. Let p and q be two positive numbers such that p + q = 2 and p⁴ + q⁴ = 272. Then p and q are roots of the equation :      (JEE Main 2021)
(a) x² – 2x + 8 =  0
(b) x² - 2x + 136 = 0
(c) x² – 2x + 16 = 0
(d) x² – 2x + 2 = 0

Ans. c
p² + q² = (p+q)² −2pq
= 4 − 2pq
Now, (p² + q²)² = p⁴ + q⁴ + 2p²q²
⇒ (4−2pq)² = 272 + 2p²q²
⇒ 16+4p²q²−16pq = 272 + 2p²q²
⇒ 2p²q²−16pq − 256 = 0
⇒ p²q² − 8pq − 128 = 0
⇒ (pq − 16)(pq + 8) = 0
⇒ pq = 16, −8
Here, pq = - 8 is not possible as p and q are positive.
∴ pq = 16
Now, the equation whose roots are p and q is
x² − 2x + 16 = 0

Q.43. For x ∈ R, the number of real roots of the equation 3x² − 4|x² − 1| + x − 1 = 0 is ________.       (JEE Advanced 2021)

Ans. 4
Given,
3x² − 4|x² − 1| + x − 1 = 0 .... (i)

For −1 ≤ x ≤ 1 i.e., x∈[−1, 1]
From Eq. (i), we get
3x² − 4(−x² + 1) + x − 1 = 0
⇒ 3x² + 4x² − 4 + x − 1 = 0
⇒ 7x² + x − 5 = 0

Here, both values of x are acceptable.
For | x | > | i.e. x ∈(− ∞, −1) ∪ (1, ∞)
From Eq. (i), we get
3x² − 4(x² − 1) + x − 1 = 0
⇒ x² − x − 3 = 0

Again here, both values of x are acceptable.
Hence, total number of solutions is 4.

Q.44. Let f(x) be a polynomial of degree 3 such that f(k) = −(2/k) for k = 2, 3, 4, 5. Then the value of 52 − 10f(10) is equal to :      (JEE Main 2021)

Ans. 26
kf(k) + 2 = λ(x−2)(x−3)(x−4)(x−5) .... (1)
put x = 0
we get λ = 1/60
Now, put λ in equation (1)
⇒ kf(k) +2 = (1/60)(x−2)(x−3)(x−4)(x−5)
Put x = 10
⇒ 10f(10) + 2 = (1/60) (8) (7) (6) (5)
⇒ 52 − 10f(10) = 52 − 26 = 26

Q.45. Let λ ≠ 0 be in R. If α and β are the roots of the equation x² − x + 2λ = 0, and α and γ are the roots of equation 3x² − 10x + 27λ = 0, then (βγ/λ) is equal to ________.     (JEE Main 2021)

Ans. 18
3α² − 10α + 27λ = 0 ..... (1)
α² − α + 2λ = 0 ...... (2)
(1) − 3(2) gives
−7α + 21λ = 0 ⇒ α = 3λ
Put α = 3λ in equation (1) we get
9λ² − 3λ + 2λ − 0
9λ² = λ ⇒ λ = (1/9) as λ ≠ 0
Now, α = 3λ ⇒ λ = 1/3
α + β = 1 ⇒ β = 2/3
α + γ = (10/3) ⇒ γ = 3

Q.46. The sum of all integral values of k (k ≠ 0) for which the equation 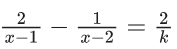 in x has no real roots, is ____.     (JEE Main 2021)

Ans. 66


⇒ k(2x − 4 − x + 1) = 2(x² − 3x + 2)
⇒ k(x − 3) = 2(x² − 3x + 2)



⇒ 2(x − 3 + 2/(x−3) + 3) ∈ (−∞, 6 − 4√2] ∪ [6 + 4√2, ∞)
for no real roots
k ∈ (6 − 4√2, 6 + 4√2)−{0}
Integral k ∈ {1, 2 ..... 11}
Sum of k = 66

Q.47. If a + b + c = 1, ab + bc + ca = 2 and abc = 3, then the value of a⁴ + b⁴ + c⁴ is equal to  _____.       (JEE Main 2021)

Ans. 13
(a + b + c)² = 1
⇒ a² + b² + c² + 2(ab + bc + ca) = 1
⇒ a² + b² + c² = – 3 ….(i)
⇒ ab + bc + ca = 2 ….(ii)
Squaring of equation (ii),
⇒ a²b² + b²c² + c²a² + 2(ab²c + bc²a + ca²b) = 4
⇒ a²b² + b²c² + c²a² + 2abc(a + b + c) = 4
⇒ a²b² + b²c² + c²a² + 6 = 4
⇒ a²b² + b²c² + c²a² = – 2 ….(iii)
Squaring of equation (i),
⇒ a⁴ + b⁴ + c⁴ + 2(a²b² + b²c² + c²a²) = 9
⇒ a⁴ + b⁴ + c⁴ – 4 = 9
⇒ a⁴ + b⁴ + c⁴ = 13

Q.48. The number of real roots of the equation e^4x − e^3x − 4e^2x − e^x + 1 = 0 is equal to _____.     (JEE Main 2021)

Ans. 2
t⁴ − t³ − 4t² − t + 1 = 0, e^x = t > 0
⇒ t² − t − 4 − (1/t) + 1/(t²) = 0
⇒ α² − α − 6 = 0, α = t + (1/t) ≥ 2
⇒ α = 3, − 2 (reject)
⇒ t + (1/t) = 3
⇒ The number of real roots = 2

Q.49. If α, β are roots of the equation x² + 5(√2)x + 10 = 0, α > β and P_n = αⁿ − βⁿ for each positive integer n, then the value of 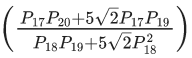 is equal to _______.     (JEE Main 2021)

Ans. 1
x² + 5√2x + 10 = 0
& P_n = αⁿ − βⁿ (Given)
Now,


Since, α + 5√2 = −10/α ..... (1)
& β + 5√2 = −10/β ....... (2)
Now, put there values in above expression = -

Q.50. The number of solutions of the equation log_(x+1)(2x² + 7x + 5) + log_(2x+5)(x+1)² − 4 = 0, x > 0, is     (JEE Main 2021)

Ans. 1
log_(x+1)(2x²+7x+5) + log_(2x+5)(x+1)² − 4 = 0
log_(x+1)(2x+5)(x+1) + 2log_(2x+5)(x+1) = 4
log_(x+1)(2x+5) + 1 + 2log_(2x+5)(x+1) = 4
Put log_(x+1)(2x+5) = t
t + (2/t) = 3 ⇒ t² − 3t + 2 = 0
t = 1, 2
log_(x+1)(2x+5) = 1 & log_(x+1)(2x+5) = 2
x+1 = 2x+3 & 2x+5 = (x+1)²
x = −4 (rejected)
x² = 4 ⇒ x = 2, −2 (rejected)
So, x = 2
No. of solution = 1

Q.51. Let α and β be two real numbers such that α + β = 1 and αβ = −1. Let p_n = (α)ⁿ + (β)ⁿ, p_n−1 = 11 and p_n+1 = 29 for some integer n ≥ 1. Then, the value of p_n² is ______.       (JEE Main 2021)

Ans. 324
Given, α + β = 1, αβ = − 1
∴ Quadratic equation with roots α, β is x² − x − 1 = 0
⇒ α² = α + 1
Multiplying both sides by αn−1
αⁿ⁺¹ = αⁿ + αⁿ⁻¹ ......(1)
Similarly,
β^{n + 1} = βⁿ + β^{n + 1} ..... (2)
Adding (1) & (2)
αⁿ⁺¹ + βⁿ⁺¹ = (αⁿ+βⁿ) + (αⁿ⁻¹ + βⁿ⁻¹)
⇒ P_n+1 = P_n + P_n−1
⇒ 29 = P_n + 11 (Given, P_{n + 1} = 29, P_{n − 1} = 11)
⇒ P_n = 18
∴ P_n² = 18² = 324

Q.52. The sum of 162^th power of the roots of the equation x³ − 2x² + 2x − 1 = 0 is ________.     (JEE Main 2021)

Ans. 3
x³ − 2x² + 2x − 1 = 0
x = 1 satisfying the equation
∴ x − 1 is factor of
x³ − 2x² + 2x − 1
= (x − 1) (x² − x + 1) = 0
x = 1,
x = 1, − ω², −ω
Sum of 162^th power of roots
= (1)¹⁶² + (−ω²)¹⁶² + (−ω)¹⁶²
= 1 + (ω)³²⁴ + (ω)¹⁶²
= 1 + 1 + 1 = 3

Q.53. The number of solutions of the equation log4(x − 1) = log₂(x − 3) is _________.       (JEE Main 2021)

Ans. 1
log₄(x−1) = log₂(x−3)
⇒ (1/2)log₂(x−1) = log₂(x−3)
⇒ log₂(x−1)^1/2= log₂(x−3)
⇒ (x−1)^1/2= log₂(x−3)
⇒ (x−1)^1/2 = x−3
⇒ x−1 = x² + 9 − 6x
⇒ x²−7x+10 = 0
⇒ (x−2)(x−5) = 0
⇒ x = 2, 5
But x ≠ 2 because it is not satisfying the domain of given equation i.e. log₂(x − 3) → its domain x > 3 finally x is 5
∴ No. of solutions = 1.

Q.54. The number of the real roots of the equation (x+1)² + |x−5| = (27/4) is ________.      (JEE Main 2021)

Ans. 2
When x>5
(x+1)² + (x−5) = 27/4
⇒ x² + 3x − 4 = 27/4
⇒ x² + 3x − 43/4 = 0
⇒ 4x² + 12x − 43 = 0




= 2.1, -5.1 [ both are rejected as x should be > 5 ]
(Therefore no solution)
For x ≤ 5
(x+1)² − (x−5) = 27/4
x² + x + 6 − 27/4 = 0
4x² + 4x − 3 = 0


∴ So, the equation have two real roots.