JEE Main Previous year questions (2021-23): Vector Algebra and Three Dimensional Geometry - 2 PDF Download

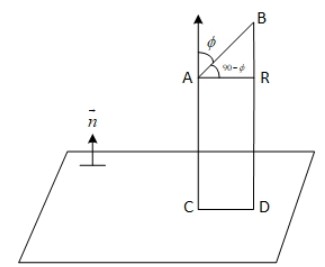
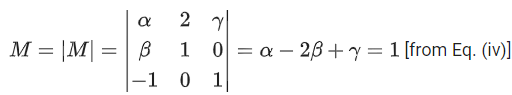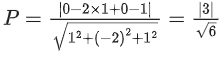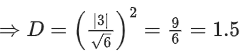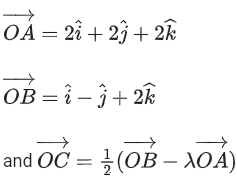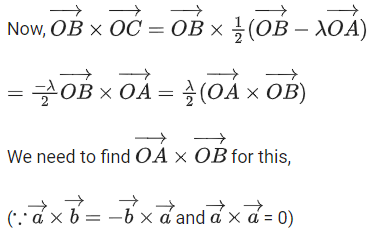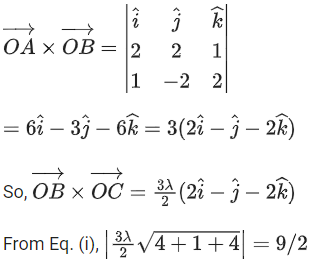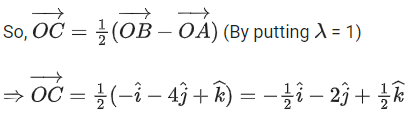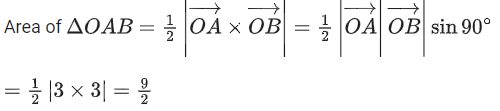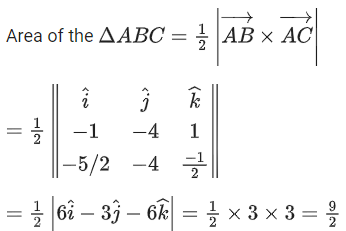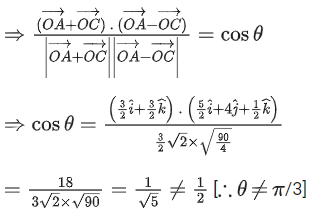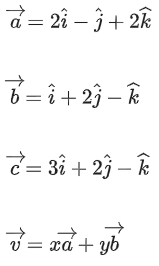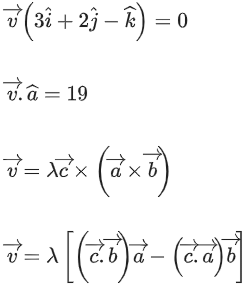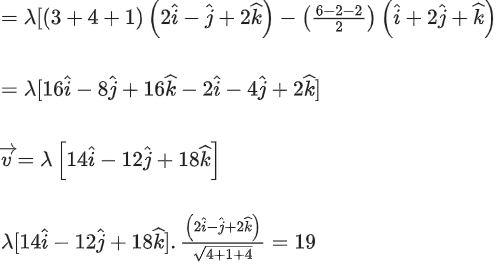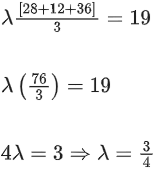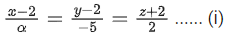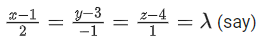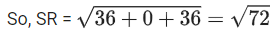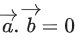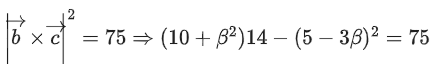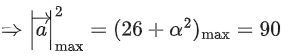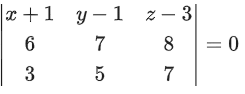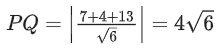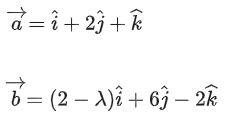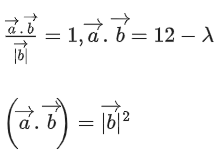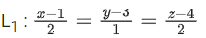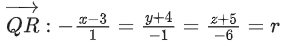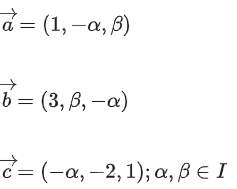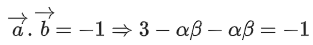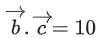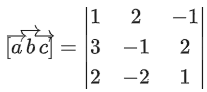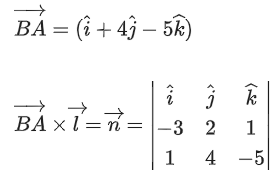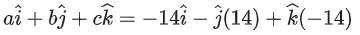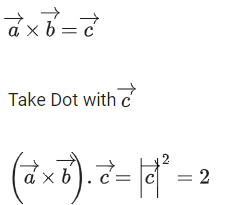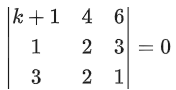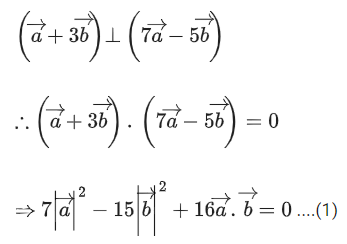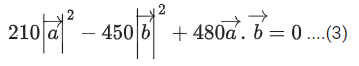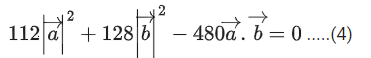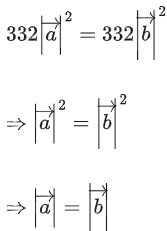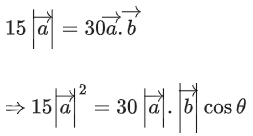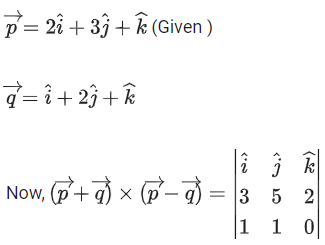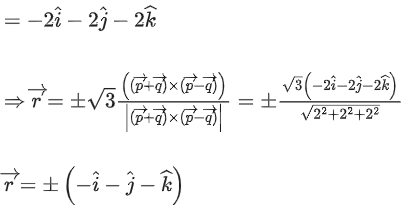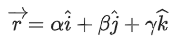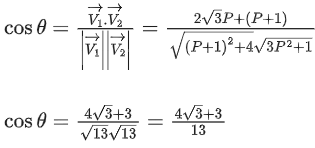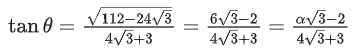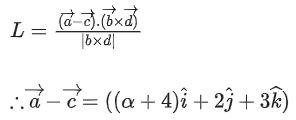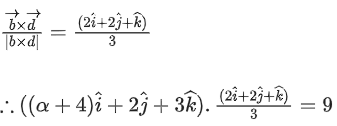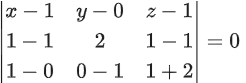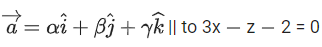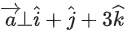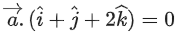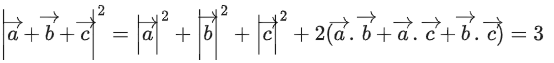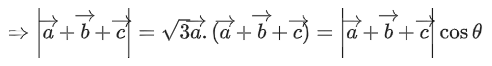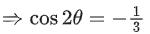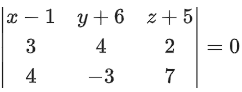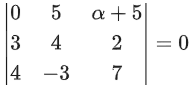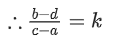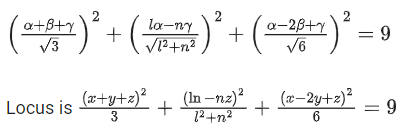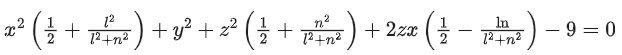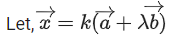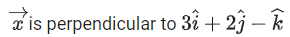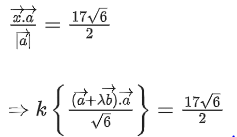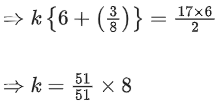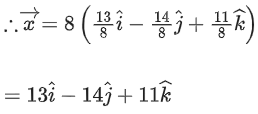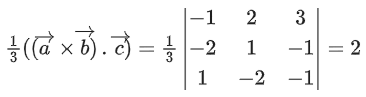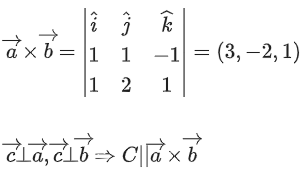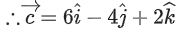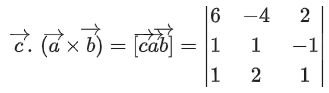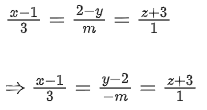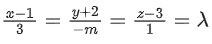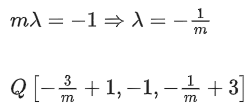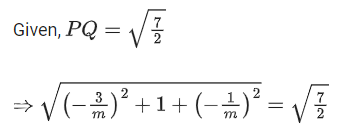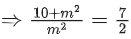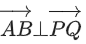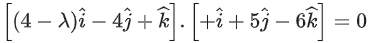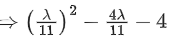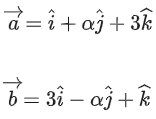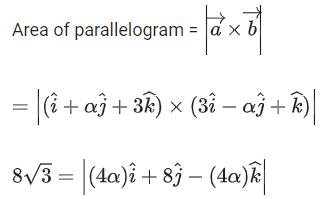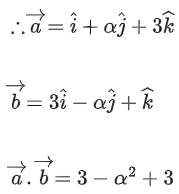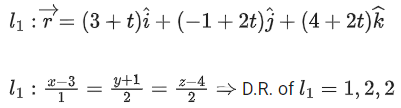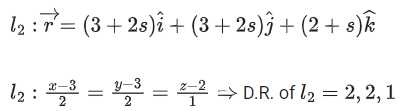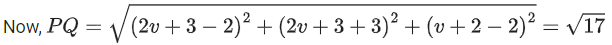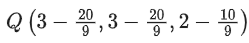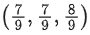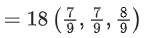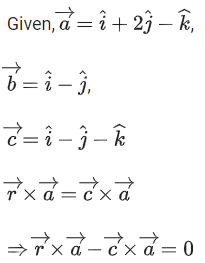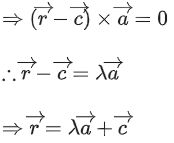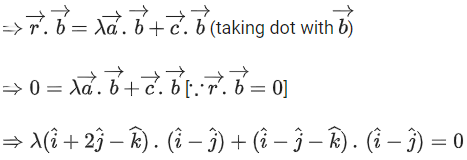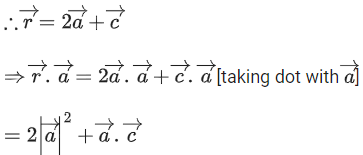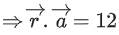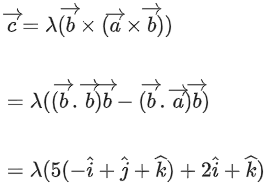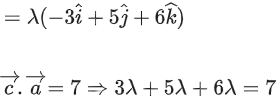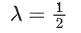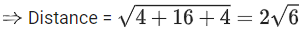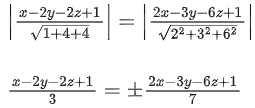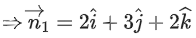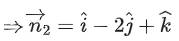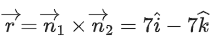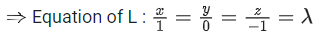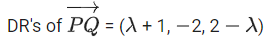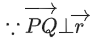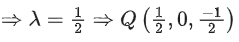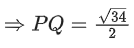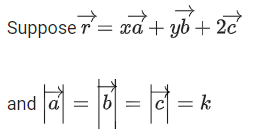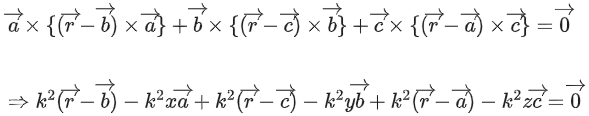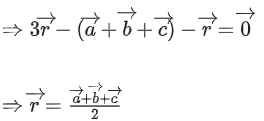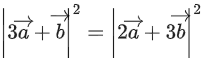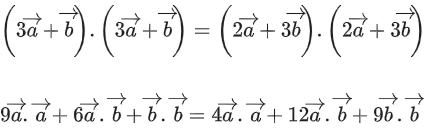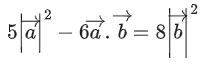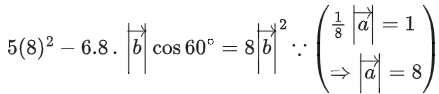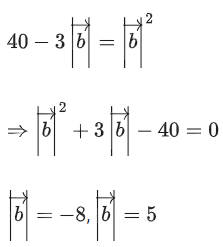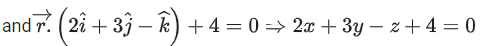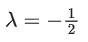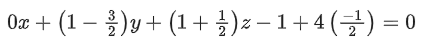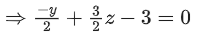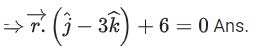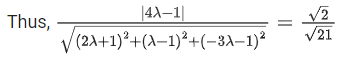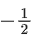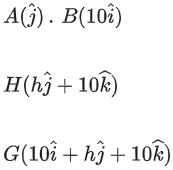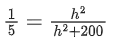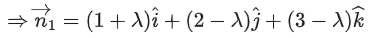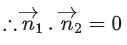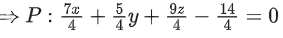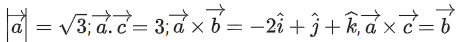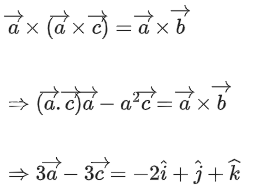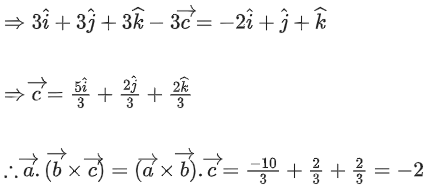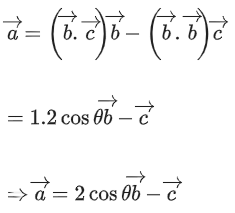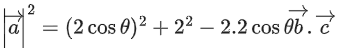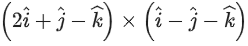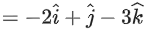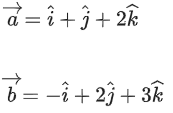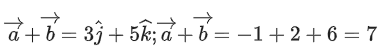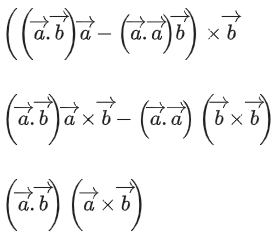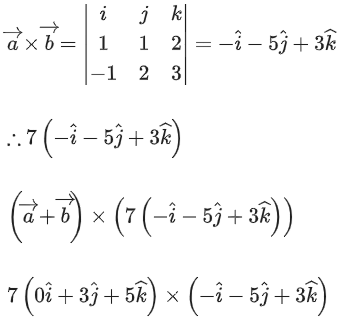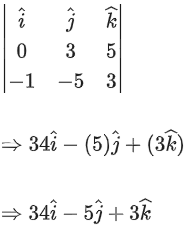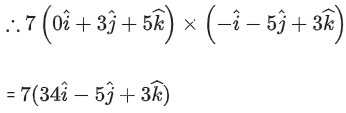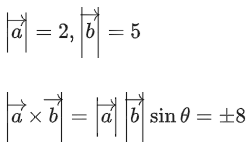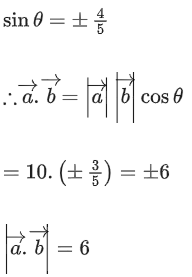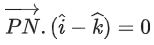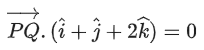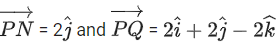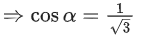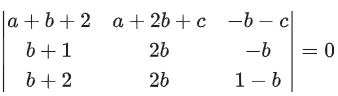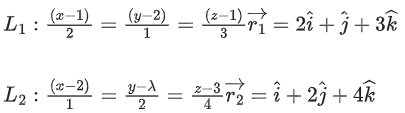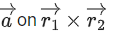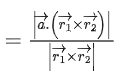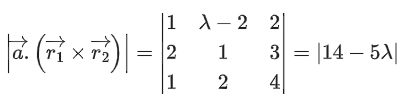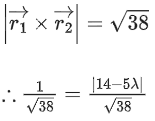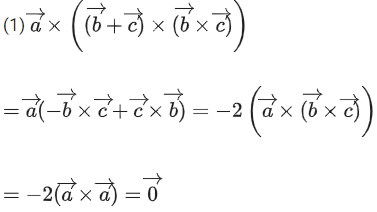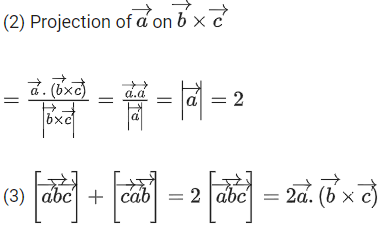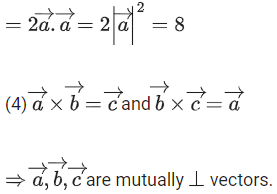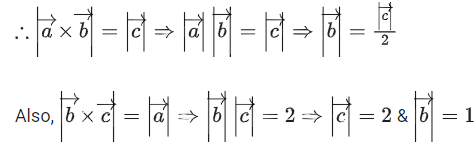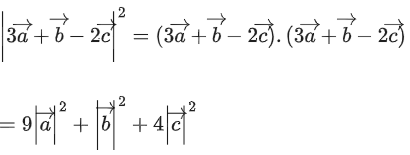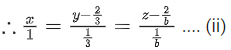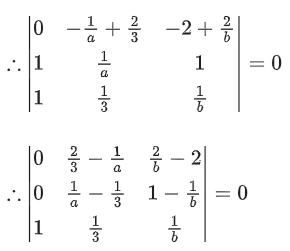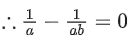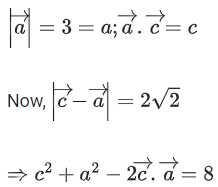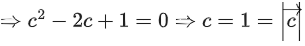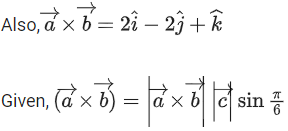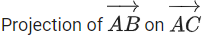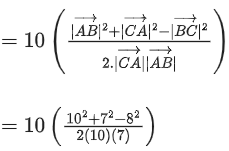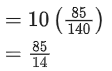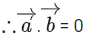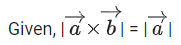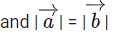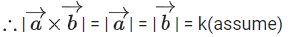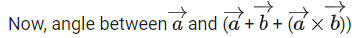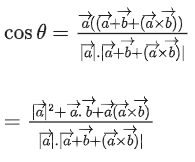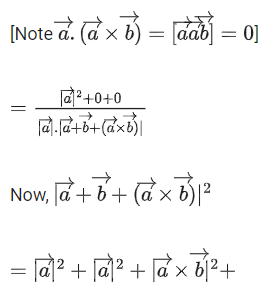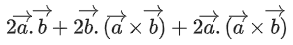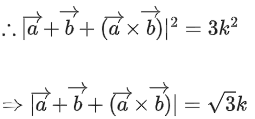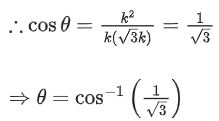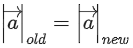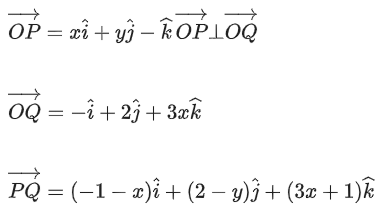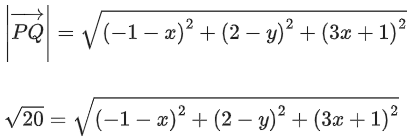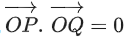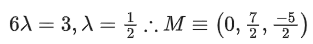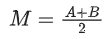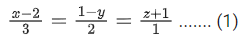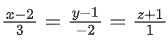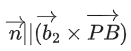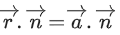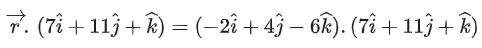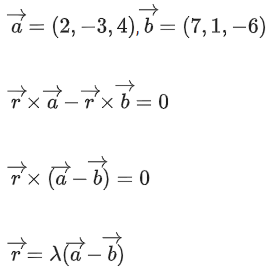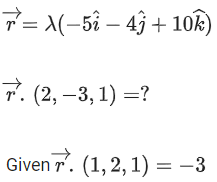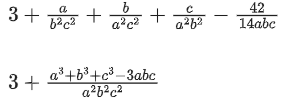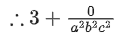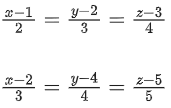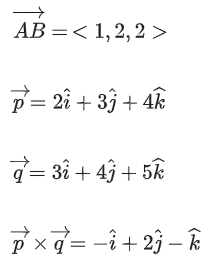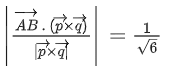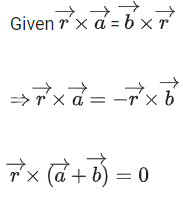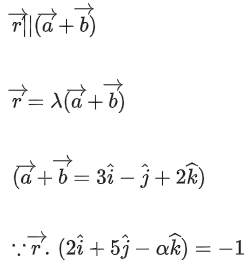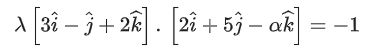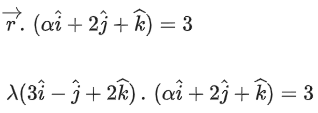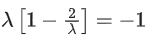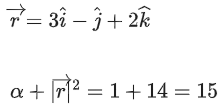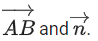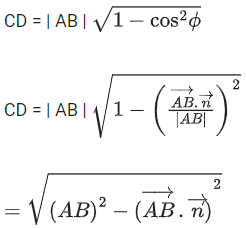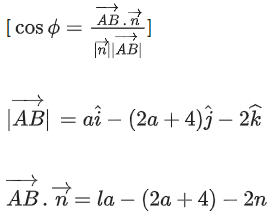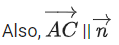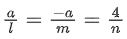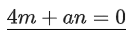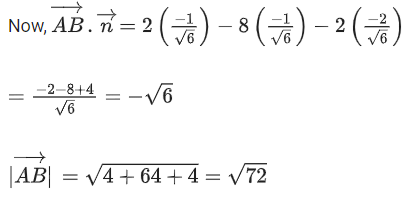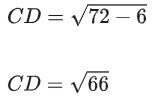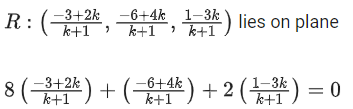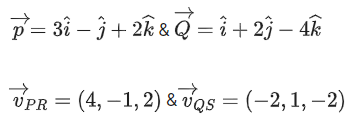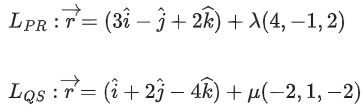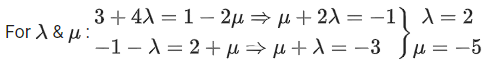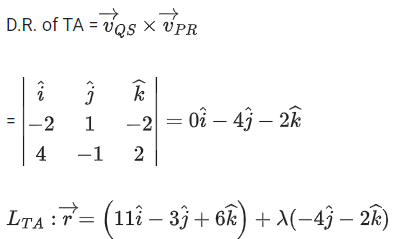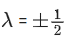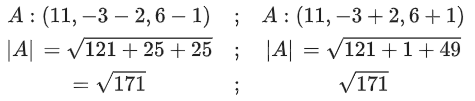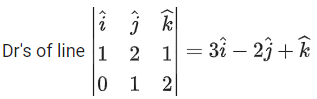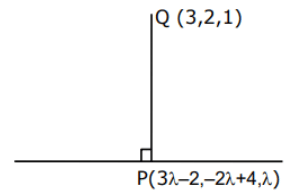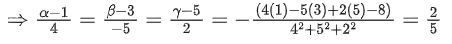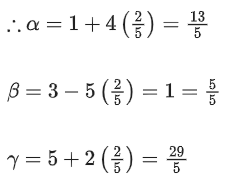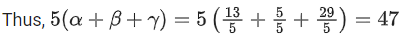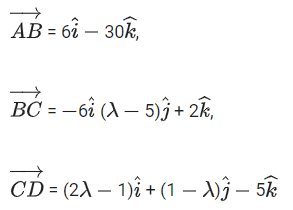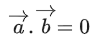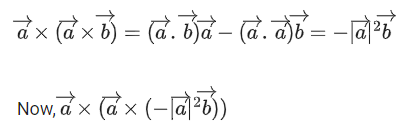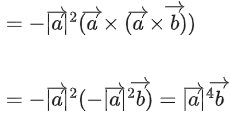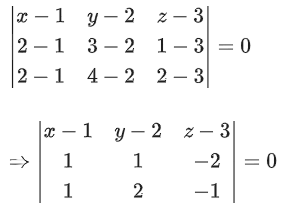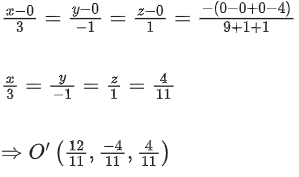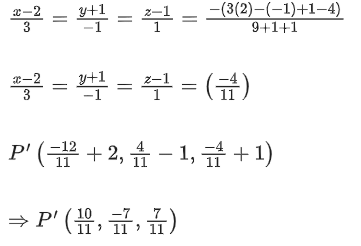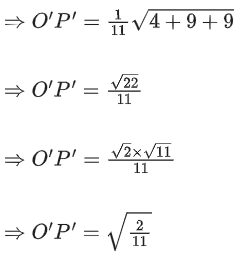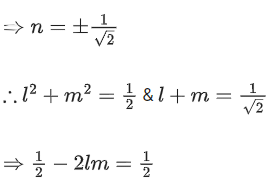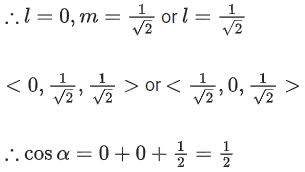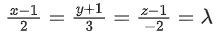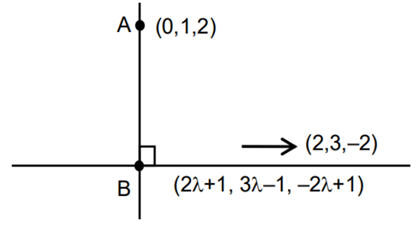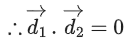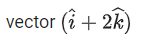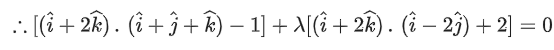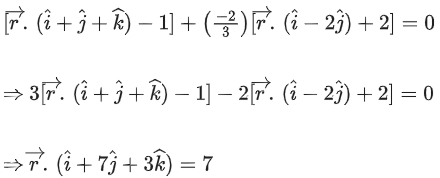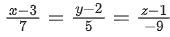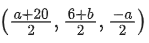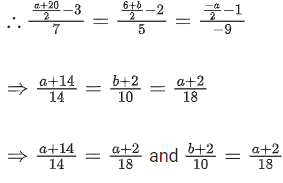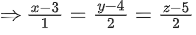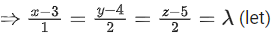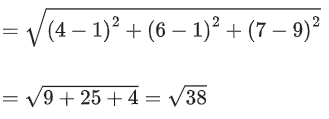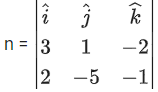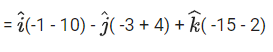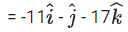Q.90. Let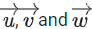be vectors in three-dimensional space, where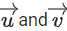are unit vectors which are not perpendicular to each other and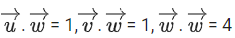
If the volume of the paralleopiped, whose adjacent sides are represented by the vectors,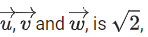 then the value of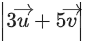is ___________.         (JEE Advanced 2021)

Ans. 7

Q.91. Let α, β and γ be real numbers such that the system of linear equations
x + 2y + 3z = α
4x + 5y + 6z = β
7x + 8y + 9z = γ − 1
is consistent. Let | M | represent the determinant of the matrix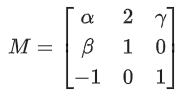

Let P be the plane containing all those (α, β, γ) for which the above system of linear equations is consistent, and D be the square of the distance of the point (0, 1, 0) from the plane P.
The value of D is _________.          (JEE Advanced 2021)

Ans. 1.5
7x + 8y + 9z − (γ − 1) = A(4x + 5y + 6z − β) + B(x + 2y + 3z − α)
On equating the coefficients,
4A + B = 7 .... (i)
5A + 2B = 8 .... (ii)
and − (γ − 1) = − Aβ − αB ..... (iii)
On solving Eqs. (i) and (ii), we get A = 2 and B = −1
From Eq. (iii), we get
− γ + 1 = − 2β − α(−1)
⇒ α − 2β + γ = 1 ..... (iv)
Now, determinant of

Equation of plane P is given by x − 2y + z = 1
Hence, perpendicular distance of the point (0, 1, 0) from the plane 

Q.92. Let α, β and γ be real numbers such that the system of linear equations
x + 2y + 3z = α
4x + 5y + 6z = β
7x + 8y + 9z = γ − 1
is consistent. Let | M | represent the determinant of the matrix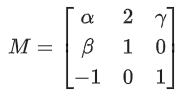

Let P be the plane containing all those (α, β, γ) for which the above system of linear equations is consistent, and D be the square of the distance of the point (0, 1, 0) from the plane P.
The value of | M | is _________.          (JEE Advanced 2021)

Ans. 1
7x + 8y + 9z − (γ − 1) = A(4x + 5y + 6z − β) + B(x + 2y + 3z − α)
On equating the coefficients,
4A + B = 7 .... (i)
5A + 2B = 8 .... (ii)
and − (γ − 1) = − Aβ − αB ..... (iii)
On solving Eqs. (i) and (ii), we get A = 2 and B = −1
From Eq. (iii), we get
− γ + 1 = − 2β − α(−1)
⇒ α − 2β + γ = 1 ..... (iv)
Now, determinant of

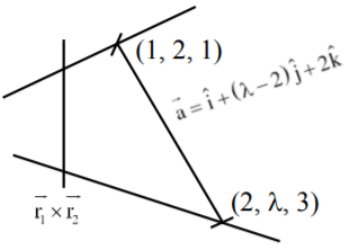
Q.93. Let O be the origin and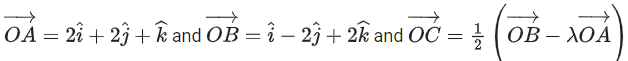for some λ > 0. If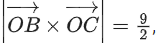then which of the following statements is (are) TRUE?          (JEE Advanced 2021)
(a) Projection of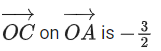
(b) Area of the triangle OAB is 9/2
(c) Area of the triangle ABC is 9/2
(d) The acute angle between the diagonals of the parallelogram with adjacent sides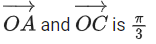

Ans. a, b, c
Given,



⇒ |λ| = 1 ⇒ λ = ±1

But λ > 0

∴ λ = 1

Option (a) 

Option (b) 

Option (c) 

Option (d)

The acute angle between the diagonals of the parallelogram with adjacent sides

Q.94. Let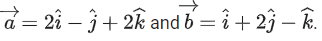Let a vector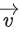be in the plane containing 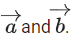. Ifis perpendicular to the vector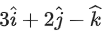and its projection on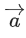is 19 units, then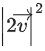is equal to _____________.          (JEE Main 2021)

Ans. 1494





= 9(49 + 36 + 81)
= 9(166)
= 1494

Q.95. Suppose the line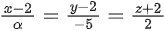lies on the plane x+3y−2z+β=0. Then (α+β) is equal to _______.          (JEE Main 2021)

Ans. 7
Given equation of line 

and plane x + 3y − 2z + β = 0 ...... (ii)

Line (i) passes through (2, 2, −2)

which lies on plane (ii).

∴ 2 + 6 + 4 + β = 0 ⇒ β = − 12

Also, given line is perpendicular to normal of the plane

α(1) − 5(3) + 2(−2) = 0 ⇒ α = 19

∴ α + β = 19 + (-12) = 19 - 12 = 7

Q.96. The square of the distance of the point of intersection of the line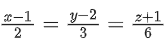and the plane 2x − y + z = 6 from the point (−1, −1, 2) is __________.          (JEE Main 2021)

Ans. 61

x = 2λ + 1, y = 3λ + 2, z = 6λ − 1
for point of intersection of line & plane
2(2λ + 1) − (3λ + 2) + (6λ − 1) = 6
7λ = 7 ⇒ λ = 1
point: (3, 5, 5)
(distance)² = (3 + 1)² + (5 + 1)² + (5 − 2)²
= 16 + 36 + 9 = 61

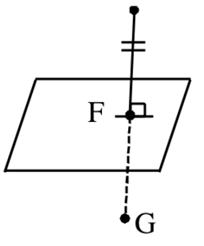
Q.97. Let S be the mirror image of the point Q(1, 3, 4) with respect to the plane 2x − y + z + 3 = 0 and let R(3, 5, γ) be a point of this plane. Then the square of the length of the line segment SR is ___________.          (JEE Main 2021)

Ans. 72

Since R(3, 5, γ) lies on the plane 2x − y + z + 3 = 0.
Therefore, 6 − 5 + γ + 3 = 0
⇒ γ = −4
Now,
dr's of line QS are 2, −1, 1
equation of line QS is

⇒ F(2λ + 1, −λ + 3, λ + 4)
F lies in the plane
⇒ 2(2λ + 1) − (−λ + 3) + (λ + 4) + 3 = 0
⇒ 4λ + 2 + λ − 3 + λ + 7 = 0
⇒ 6λ + 6 = 0 ⇒ λ = −1
⇒ F(−1, 4, 3)
Since, F is mid-point of QS.
Therefore, coordinated of S are (−3, 5, 2)

SR² = 72.

Q.98. Let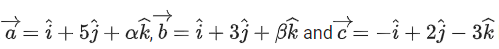be three vectors such that,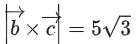andis perpendicular to b Then the greatest amongst the values of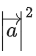is _____________.          (JEE Main 2021)

Ans. 90
Since,
1 + 15 + αβ = 0 ⇒ αβ = −16 .... (1)
Also,

⇒ 5β² + 30β + 40 = 0
⇒ β = −4, −2
⇒ α = 4, 8

Q.99. Let Q be the foot of the perpendicular from the point P(7, −2, 13) on the plane containing the lines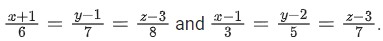Then (PQ)², is equal to ___________.          (JEE Main 2021)

Ans. 96
Containing the line
9(x + 1) − 18(y − 1) + 9(z − 3) = 0
x − 2y + z = 0

PQ² = 96

Q.100. If the projection of the vectoron the sum of the two vectors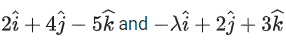is 1, then λ is equal to __________.          (JEE Main 2021)

Ans. 5


λ² − 24λ + 144 = λ² − 4λ + 4 + 40
20λ = 100 ⇒ λ = 5 

Q.101. Let the line L be the projection of the line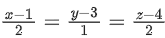in the plane x − 2y − z = 3. If d is the distance of the point (0, 0, 6) from L, then d² is equal to _______________.          (JEE Main 2021)

Ans. 26

for foot of ⊥ r of (1, 3, 4) on x − 2y − z − 3 = 0
(1 + t) − 2(3 − 2t) − (4 − t) − 3 = 0
⇒ t = 2
So foot of ⊥ r(3, −1, 2) & point of intersection of L₁ with plane is (−11, −3, −8)
dr's of L is <14, 2, 10>
≅ <7, 1, 5>
Image

Q.102. The distance of the point P(3, 4, 4) from the point of intersection of the line joining the points. Q(3, −4, −5) and R(2, −3, 1) and the plane 2x + y + z = 7, is equal to ______________.          (JEE Main 2021)

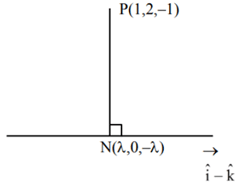
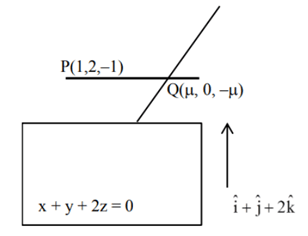
Ans. 7

⇒ (x, y, z) ≡ (r + 3, −r − 4, −6r − 5)
Now, satisfying it in the given plane.
We get r = −2
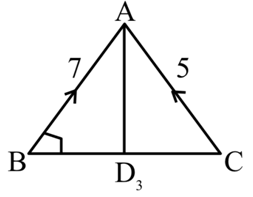
so, required point of intersection is T(1, −2, 7).
Hence, PT = 7

Q.103. Let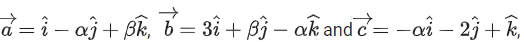 where α and β are integers. If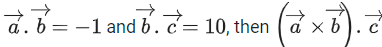is equal to ___________.          (JEE Main 2021)

Ans. 9


⇒ αβ = 2
Possible value of
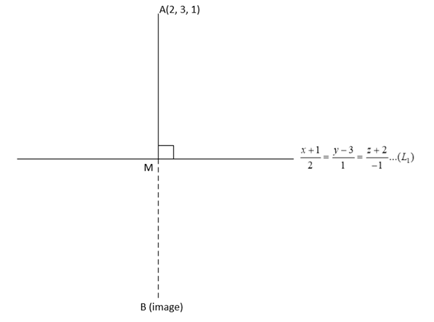
α and β
1      2
2      1
−1 −2
−2  −1

⇒ −3α − 2β − α = 10
⇒ 2α + β + 5 = 0
∴ α = −2; β = −1

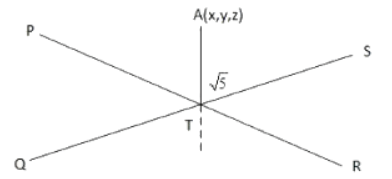
= 1(−1 + 4) − 2(3 − 4) − 1(−6 + 2)
= 3 + 2 + 4 = 9

Q.104. Let a plane P pass through the point (3, 7, −7) and contain the line, 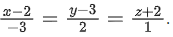If distance of the plane P from the origin is d, then d² is equal to ______________.          (JEE Main 2021)

Ans. 3


a = 1, b = 1, c = 1
Plane is (x − 2) + (y − 3) + (z + 2) = 0
⇒ x + y + z − 3 = 0
∴ d = √3 ⇒ d² = 3

Q.105. Let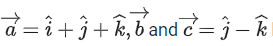be three vectors such that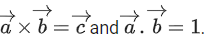If the length of projection vector of the vector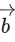on the vector 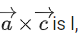then the value of 3l² is equal to _____________.          (JEE Main 2021)

Ans. 2


3l² = 2

Q.106. If the lines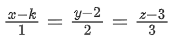and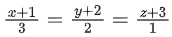are co-planar, then the value of k is _____________.          (JEE Main 2021)

Ans. 1

⇒ (k + 1)[2 − 6] − 4[1 − 9] + 6[2 − 6] = 0 
⇒ k = 1

Q.107. If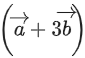is perpendicular to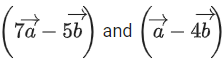is perpendicular to 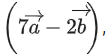then the angle between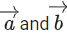(in degrees) is _______________.          (JEE Main 2021)

Ans. 60


Equation (1) × 30 

Equation (2) × 16 

from (3) & (4) 

From equation (2), 

cos⁡θ = 15/30 = 1/2 
∴ θ = 60^∘

Q.108. Let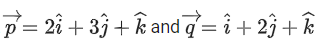be two vectors. If a vector 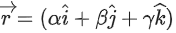is perpendicular to each of the vectors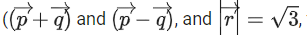then |α|+|β|+|γ| is equal to _______________.          (JEE Main 2021)

Ans. 3


According to question 

So, |α| = 1, |β| = 1, |γ| = 1
⇒ |α|+|β|+|γ| = 3

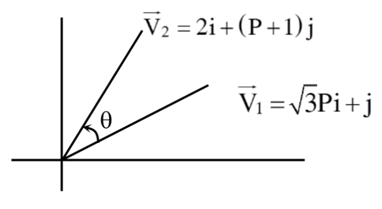
Q.109. For p > 0, a vectoris obtained by rotating the vector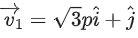 by an angle θ about origin in counter clockwise direction. If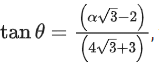then the value of α is equal to _____________.          (JEE Main 2021)

Ans. 6


3P² + 1 = 4 + (P + 1)²
2P² − 2P − 4 = 0 ⇒ P² − P − 2 = 0
P = 2, −1 (rejected) 


⇒ α = 6

Q.110. If the shortest distance between the lines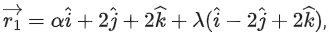λ ∈ R, α > 0 and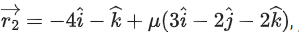μ ∈ R is 9, then α is equal to ____________.          (JEE Main 2021)

Ans. 6
shortest distance between two lines is 


or α = 6 

Q.111. Let P be a plane passing through the points (1, 0, 1), (1, −2, 1) and (0, 1, −2). Let a vector 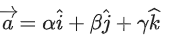be such that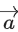is parallel to the plane P, perpendicular to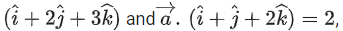then (α − β + γ)² equals ____________.          (JEE Main 2021)

Ans. 81
Equation of plane : 

⇒ 3x − z − 2 = 0

⇒ 3α − 8 = 0 ..... (1)

⇒ α + 2β + 38 = 0 ...... (2)

⇒ α + β + 28 = 2 ........ (3_)
On solving 1, 2 & 3
α = 1, β = −5, 8 = 3
So, (α − β + 8) = 81 

Q.112. Let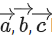be three mutually perpendicular vectors of the same magnitude and equally inclined at an angle θ, with the vector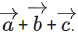Then 36cos²2θ is equal to ___________.          (JEE Main 2021)

Ans. 4

⇒ 1 = √3 cos⁡θ

⇒ 36cos²2θ = 4

Q.113. Let P be a plane containing the line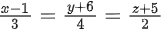and parallel to the line 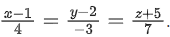If the point (1, −1, α) lies on the plane P, then the value of |5α| is equal to ____________.          (JEE Main 2021)

Ans. 38
Equation of required plane is

Since, (1, −1, α) lies on it,

So, replace x by 1, y by (−1) and z and α.

⇒ 5α + 38 = 0 ⇒ 5α = −38

∴ |5α| = |−38| = 38

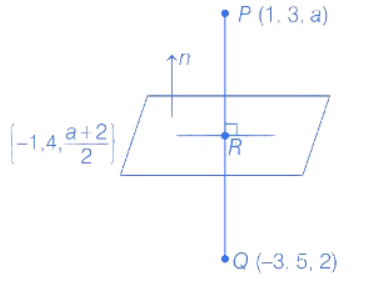
Q.114. Let the mirror image of the point (1, 3, a) with respect to the plane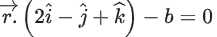 be (−3, 5, 2). Then, the value of | a + b | is equal to ____________.          (JEE Main 2021)

Ans. 1
Given equation of plane in vector form is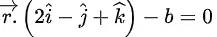 

Its Cartesian form will be

2x − y + z = b ...... (i)

∵ R is the mid-point of PQ.

∵ R lies on the plane (i).

⇒ a = 2b + 10 ....... (ii)

∵ Direction ratio's of QP is (1 − (−3), 3 − 5, a − 2)

i.e. (4, −2, a − 2)

and direction ratios of normal to the given plane are (2, −1, 1)

∵ n and QP are parallel.

∴ a − 2 = 2 ⇒ a = 4

From Eq. (ii), b = −3

∴ |a + b| = |4 − 3| = |1| = 1

Q.115. The equation of the planes parallel to the plane x − 2y + 2z − 3 = 0 which are at unit distance from the point (1, 2, 3) is ax + by + cz + d = 0. If (b − d) = K(c − a), then the positive value of K is          (JEE Main 2021)

Ans. 4
The equation of the planes parallel to the plane x − 2y + 2z − 3 = 0
x − 2y + 2z + λ = 0
Now given
|λ + 3| = 3
λ + 3 = ±3 ⇒ λ = 0, −6
So planes are: x − 2y + 2z − 6 = 0
and x − 2y + 2z = 0
b − d = −2 + 6 = 4
c − a = 2 − 1 = 1

⇒ k = 4

Q.116. Let the plane ax + by + cz + d = 0 bisect the line joining the points (4, −3, 1) and (2, 3, −5) at the right angles. If a, b, c, d are integers, then the minimum value of (a² + b² + c² + d²) is          (JEE Main 2021)

Ans. 28
Normal of plane =
a = −2, b = 6, c = −6
& equation of plane is
−2x + 6y − 6z + d = 0
M(3, 0, −2) is the midpoint of the line which present on the plane
which satisfy the plane
∴ d = −6

Now equation of plane is
−2x + 6y − 6z − 6 = 0
x − 3y + 3z + 3 = 0
⇒ (a² + b² + c² + d²)_min = 1² + 9 + 9 + 9 = 28 

Q.117. Let P be an arbitrary point having sum of the squares of the distances from the planes x + y + z = 0, lx − nz = 0 and x − 2y + z = 0, equal to 9. If the locus of the point P is x² + y² + z² = 9, then the value of l − n is equal to _________.          (JEE Main 2021)

Ans. 0
Let point P is (α, β, γ)


Since its given that x² + y² + z² = 9
After solving l = n,
then l − n = 0

Q.118. Let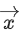be a vector in the plane containing vectors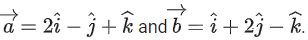If the vector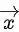is perpendicular to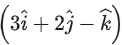and its projection on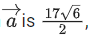then the value of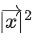is equal to __________.          (JEE Main 2021)

Ans. 486


I. k{(2 + λ)3 + (2λ − 1)2 + (1 − λ)(−1) = 0
⇒ 8λ + 3 = 0
λ = −3/8
II. Also projection ofthereforex→.a→|a→|=1762


k = 8

Q.119.


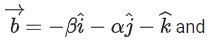
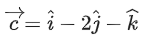
such that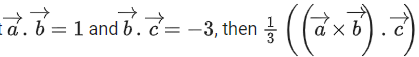is equal to _____________.          (JEE Main 2021)

Ans. 2
= 1 ⇒ −αβ − αβ − 3 = 1
⇒ αβ = −2 .... (i)
= −3 ⇒ −β + 2α + 1 = −3
2α − β = −4 ..... (ii)
Solving (i) & (ii) α = −1, β = 2, 

Q.120. If the equation of the plane passing through the line of intersection of the planes 2x − 7y + 4z − 3 = 0, 3x − 5y + 4z + 11 = 0 and the point (−2, 1, 3) is ax + by + cz − 7 = 0, then the value of 2a + b + c − 7 is ____________.          (JEE Main 2021)

Ans. 4
Equation of plane can be written using family of planes: P₁ + λP₂ = 0
(2x − 7y + 4z − 3) + λ (3x − 5y + 4z + 11) = 0
It passes through (−2, 1, 3)
∴ (−4 + 7 + 12 − 3) + λ (−6 − 5 + 12 + 11) = 0
−2 + λ (12) = 0
λ = 1/6
∴ 12x − 42y + 24z − 18 + 3x − 5y + 4z + 11 = 0
15x − 47y + 28z − 7 = 0
∴ a = 15, b = −47, c = 28
∴ 2a + b + c − 7 = 30 − 47 + 28 − 7 = 4 

Q.121. Let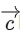be a vector perpendicular to the vectors,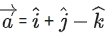andthen the value of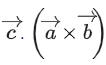is equal to __________.          (JEE Main 2021)

Ans. 28


⇒ 3λ − 2λ + 3λ = 8
⇒ 4λ = 8 ⇒ λ = 2

⇒ 18 + 8 + 2 = 28 

Q.122. If the distance of the point (1, −2, 3) from the plane x + 2y − 3z + 10 = 0 measured parallel to the line,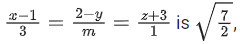then the value of |m| is equal to _________.          (JEE Main 2021)

Ans. 2

Given line L, 

∴ D.R of line = <3, -m, 1>
D.R of parallel line PQ will also be same.
∴ Equation of line PQ, 

Pt. Q(3λ + 1, −mλ − 2, λ + 3) lie on plane
(3λ + 1) + 2(−mλ − 2) − 3(λ + 3) + 10 = 0
⇒ 3λ − 2mλ − 3λ + 1 − 4 − 9 + 10 = 0
⇒ −2mλ = 2



⇒ 20 + 2m² = 7m² 
⇒ m² = 4 ⇒ |m| = 2 

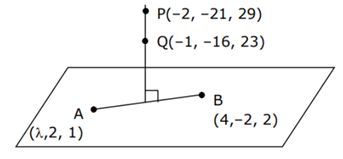
Q.123. Let (λ, 2, 1) be a point on the plane which passes through the point (4, −2, 2). If the plane is perpendicular to the line joining the points (−2, −21, 29) and (−1, −16, 23), then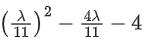is equal to __________.          (JEE Main 2021)

Ans. 8



4 − λ − 20 − 6 = 0
⇒ λ = -22
Now, λ/11 = −2

⇒ 4 + 8 − 4 = 8

Q.124. LetIf the area of the parallelogram whose adjacent sides are represented by the vectors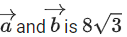square units, then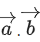is equal to __________.          (JEE Main 2021)

Ans. 2


(64)(3) = 16α² + 64 + 16α²
(64)(3) = 32α² + 64
6 = α² + 2
α² = 4

= 6 − α²
= 6 − 4
= 2

Q.125. A line 'l' passing through origin is perpendicular to the lines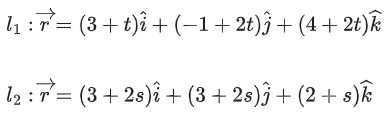

If the co-ordinates of the point in the first octant on 'l₂‘ at a distance of √17 from the point of intersection of 'l' and 'l₁' are (a, b, c) then 18(a + b + c) is equal to ___________.          (JEE Main 2021)

Ans. 44


D.R. of l is ⊥ to l₁ & k₂
∴ D.R. of l||(l₁ × l₂) ⇒ (−2, 3 − 2)
Solving l & l₁
(2λ, −3λ, 2λ) = (μ + 3, 2μ − 1, 2μ + μ)
⇒ 2λ = μ + 3
−3λ = 2μ − 1
2λ = 2μ + 4
⇒ μ + 3 = 2μ + 4
μ = −1
λ = 1
P(2, −3, 2) {intersection point}
Let, Q(2v + 3, 2v + 3, v + 2) be point on l₂

⇒ (2v + 1)² + (2v + 6)² + (v)² = 17
⇒ 9v² + 28v + 36 + 1 − 17 = 0
⇒ 9v² + 28v + 20 = 0
⇒ 9v² + 18v + 10v + 20 = 0
⇒ (9v + 10)(v + 2) = 0
⇒ v = −2 (rejected), (accepted)


∴ 18(a + b + c)

= 44

Q.126. Let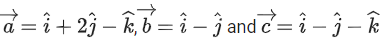be three given vectors. If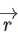is a vector such that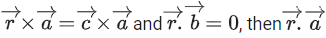is equal to __________.          (JEE Main 2021)

Ans. 12

⇒ λ(1 − 2) + 2 = 0

⇒ λ = 2

= 2(1 + 4 + 1) + (1 − 2 + 1)

Q.127. Let three vectors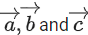be such that is coplanar with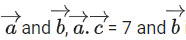is perpendicular to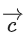, where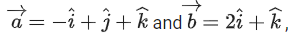then the value of 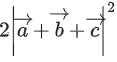is _____.          (JEE Main 2021)

Ans. 75



 

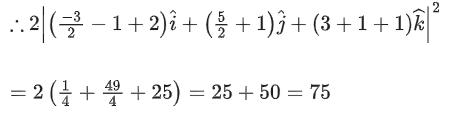
Q.128. The distance of line 3y − 2z − 1 = 0 = 3x − z + 4 from the point (2, −1, 6) is:          (JEE Main 2021)
(a) 26
(b) 25
(c) 26
(d) 42

Ans. c
3y − 2z − 1 = 0 = 3x − z + 4
3y − 2z − 1 = 0
D.R's ⇒ (0, 3, −2)
3x − z + 4 = 0
D.R's ⇒ (3, −1, 0)
Let DR's of given line are a, b, c
Now, 3b − 2c = 0 & 3a − c = 0
∴ 6a = 3b = 2c
a : b : c = 3 : 6 : 9
Any point on line
3K − 1, 6K + 1, 9K + 1
Now, 3(3K − 1) + 6(6K + 1)1 + 9(9K + 1) = 0
⇒ K = 1/3
Point on line ⇒ (0, 3, 4)
Given point (2, −1, 6)

Option (c) 

Q.129. Let the acute angle bisector of the two planes x − 2y − 2z + 1 = 0 and 2x − 3y − 6z + 1 = 0 be the plane P. Then which of the following points lies on P?          (JEE Main 2021)
(a)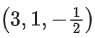
(b)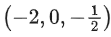
(c) (0, 2, −4)
(d) (4, 0, −2)

Ans. b
P₁: x − 2y − 2z + 1 = 0
P₂: 2x − 3y − 6z + 1 = 0

Since a₁a₂ + b₁b₂ + c₁c₂ = 20 > 0
∴ Negative sign will give acute bisector
7x − 14y − 14z + 7 = −[6x − 9y − 18z + 3]
⇒ 13x − 23y − 32z + 10 = 0
satisfy it ∴ Ans. (b)

Q.130. The distance of the point (−1, 2, −2) from the line of intersection of the planes 2x + 3y + 2z = 0 and x − 2y + z = 0 is:          (JEE Main 2021)
(a) 1/√2
(b) 5/2
(c) √42/2
(d) √34/2

Ans. d
P₁ : 2x + 3y + 2z = 0

P₂ : x − 2y + z = 0

Direction vector of line L which is line of intersection of P₁ & P₂

DR's of L are (1, 0, −1)




⇒ (λ + 1)(1) + (−2)(0) + (2 − λ)(−1) = 0

Q.131. Let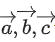three vectors mutually perpendicular to each other and have same magnitude. If a vector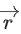satisfies. is equal to:          (JEE Main 2021)
(a)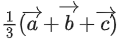
(b)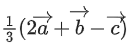
(c)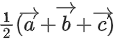
(d)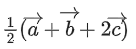

Ans. c

Q.132. Let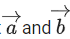be two vectors such that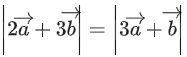and the angle between 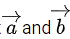is 60^∘. If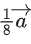is a unit vector, then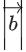is equal to:          (JEE Main 2021)
(a) 4
(b) 6
(c) 5
(d) 8

Ans. c





(rejected) 

Q.133. Let the equation of the plane, that passes through the point (1, 4, −3) and contains the line of intersection of the planes 3x − 2y + 4z − 7 = 0 and x + 5y − 2z + 9 = 0, be αx + βy + γz + 3 = 0, then α + β + γ is equal to:          (JEE Main 2021)
(a) −23
(b) −15
(c) 23
(d) 15

Ans. a
3x − 2y + 4z − 7 + λ(x + 5y − 2z + 9) = 0
(3 + λ)x + (5λ − 2)y + (4 − 2λ)z + 9λ − 7 = 0
passing through (1, 4, −3)
⇒ 3 + λ + 20λ − 8 − 12 + 6λ + 9λ − 7 = 0
⇒ λ = 23
⇒ equation of plane is
−11x − 4y − 8z + 3 = 0
⇒ α + β + γ = −23 

Q.134. The equation of the plane passing through the line of intersection of the planes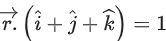and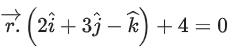and parallel to the x-axis is:          (JEE Main 2021)
(a)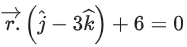
(b)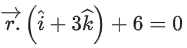
(c)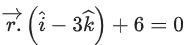
(d)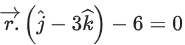

Ans. a
Equation of planes are 


equation of planes through line of intersection of these planes is:
(x + y + z − 1) + λ(2x + 3y − z + 4) = 0
⇒ (1 + 2λ)x + (1 + 3λ)y + (1 − λ)z − 1 + 4λ = 0
But this plane is parallel to x-axis whose direction are (1, 0, 0)
∴ (1 + 2λ)1 + (1 + 3λ)0 + (1 − λ)0 = 0

∴ Required plane is


⇒ y − 3z + 6 = 0

Q.135. Equation of a plane at a distance 2/√21 from the origin, which contains the line of intersection of the planes x − y − z − 1 = 0 and 2x + y − 3z + 4 = 0, is:          (JEE Main 2021)
(a) 3x − y − 5z + 2 = 0
(b) 3x − 4z + 3 = 0
(c) −x + 2y + 2z − 3 = 0
(d) 4x − y − 5z + 2 = 0

Ans. d
Required equation of plane
P₁ + λP₂ = 0
(x − y − z − 1) + λ(2x + y − 3z + 4) = 0
Given that its dist. From origin is 2/√21

⇒ 21(4λ − 1)² = 2(14λ² + 8λ + 3)
⇒ 336λ² − 168λ + 21 = 28λ² + 16λ + 6
⇒ 308λ² − 184λ + 15 = 0
⇒ 308λ² − 154λ − 30λ + 15 = 0
⇒ (2λ − 1)(154λ − 15) = 0
⇒ λ = 1/2 or 15/154
for λ = 1/2 reqd. plane is 4x − y − 5z + 2 = 0

Q.136. Let P be the plane passing through the point (1, 2, 3) and the line of intersection of the planes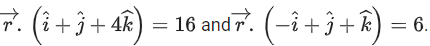Then which of the following points does NOT lie on P?          (JEE Main 2021)
(a) (3, 3, 2)
(b) (6, −6, 2)
(c) (4, 2, 2)
(d) (−8, 8, 6)

Ans. c
(x + y + 4z − 16) + λ(−x + y + z − 6) = 0
Passes through (1, 2, 3)
−1 + λ(−2) ⇒ λ =
2(x + y + 4z − 16) − (−x + y + z − 6) = 0
3x + y + 7z − 26 = 0

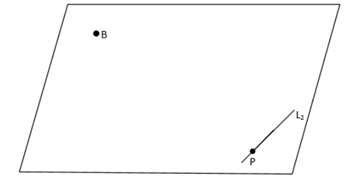
Q.137. A hall has a square floor of dimension 10 m × 10 m (see the figure) and vertical walls. If the angle GPH between the diagonals AG and BH is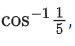then the height of the hall (in meters) is:          (JEE Main 2021)
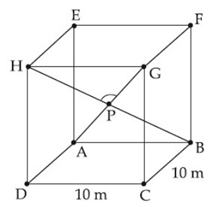(a) 5
(b) 2√10
(c) 5√3
(d) 5√2

Ans. d



4h² = 200 ⇒ h = 5√2

Q.138. A plane P contains the line x + 2y + 3z + 1 = 0 = x − y − z − 6, and is perpendicular to the plane −2x + y + z + 8 = 0. Then which of the following points lies on P?          (JEE Main 2021)
(a) (−1, 1, 2)
(b) (0, 1, 1)
(c) (1, 0, 1)
(d) (2, −1, 1)

Ans. b
Equation of plane P can be assumed as
P : x + 2y + 3z + 1 + λ (x − y − z − 6) = 0
⇒ P : (1 + λ)x + (2 − λ)y + (3 − λ)z + 1 − 6λ = 0


⇒ 2(1 + λ) − (2 − λ) − (3 − λ) = 0
⇒ 2 + 2λ − 2 + λ − 3 + λ = 0 ⇒ λ = 3/4

⇒ 7x + 5y + 9z = 14
(0, 1, 1) lies on P.

Q.139. Let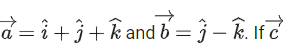is a vector such thatis equal to:          (JEE Main 2021)
(a) −2
(b) −6
(c) 6
(d) 2

Ans. a

Cross with

Q.140. Let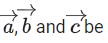three vectors such that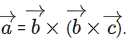If magnitudes of the vectors 1 and 2 respectively and the angle between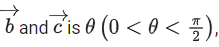then the value of 1 + tanθ is equal to:          (JEE Main 2021)
(a)
(b) 2
(c) 1
(d)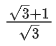

Ans. b


⇒ 2 = 4cos²θ + 4 − 4cos⁡θ.2cos⁡θ
⇒ −2 = −4cos²θ
⇒ cos²θ = 1/2
⇒ sec²θ = 2
⇒ tan²θ = 1
⇒ θ = π/4
∴ 1 + tan⁡θ = 2

Q.141. For real numbers α and β ≠ 0, if the point of intersection of the straight lines 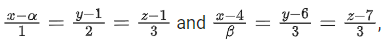lies on the plane x + 2y − z = 8, then α − β is equal to:          (JEE Main 2021)
(a) 5
(b) 9
(c) 3
(d) 7

Ans. d
First line is (ϕ + α, 2ϕ + 1, 3ϕ + 1)
and second line is (qβ + 4, 3q + 6, 3q + 7)
For intersection
ϕ + α = qβ + 4 ...... (i)
2ϕ + 1 = 3q + 6 .... (ii)
3ϕ + 1 = 3q + 7 ...... (iii)
for (ii) & (iii) ϕ = 1, q = −1
So, from (i) α + β = 3
Now, point of intersection is (α + 1, 3, 4)
It lies on the plane.
Hence, α = 5 & β = −2 

Q.142. Let the plane passing through the point (−1, 0, −2) and perpendicular to each of the planes 2x + y − z = 2 and x − y − z = 3 be ax + by + cz + 8 = 0. Then the value of a + b + c is equal to:          (JEE Main 2021) 
(a) 3
(b) 8
(c) 5
(d) 4

Ans. d
Normal of req. plane

Equation of plane
−2(x + 1) + 1(y − 0) − 3(z + 2) = 0
−2x + y − 3z − 8 = 0
2x − y + 3z + 8 = 0
a + b + c = 4

Q.143. LetThen the vector product 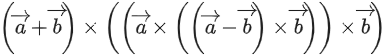is equal to:          (JEE Main 2021) 
(a)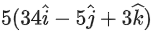
(b)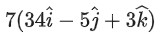
(c)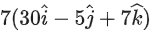
(d)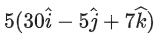

Ans. b

Q.144. If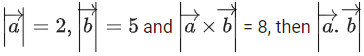is equal to:          (JEE Main 2021) 
(a) 6
(b) 4
(c) 3
(d) 5

Ans. a

Q.145. Let a, b and c be distinct positive numbers. If the vectors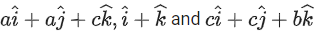are co-planar, then c is equal to:          (JEE Main 2021)
(a)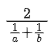
(b)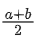
(c)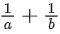
(d)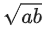

Ans. d
Because vectors are coplanar

Q.146. Let the foot of perpendicular from a point P(1, 2, −1) to the straight line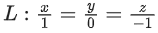be N. Let a line be drawn from P parallel to the plane x + y + 2z = 0 which meets L at point Q. If α is the acute angle between the lines PN and PQ, then cosα is equal to ________________.          (JEE Main 2021)
(a)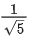
(b)
(c)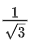
(d)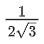

Ans. c


⇒ N(1, 0, −1) 
Now,


⇒ μ = − 1 
⇒ Q (−1, 0, 1)

Q.147. Let the vectors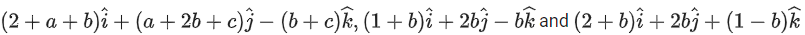a, b, c, ∈ R be co-planar. Then which of the following is true?          (JEE Main 2021)
(a) 2b = a + c
(b) 3c = a + b
(c) a = b + 2c
(d) 2a = b + c

Ans. a
If the vectors are co-planar, 

Now, R₃ → R₃ − R₂, R₁ → R₁ − R₂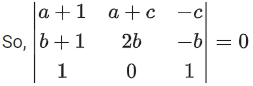
 
= (a + 1)2b − (a + c)(2b + 1) − c(−2b)
= 2ab + 2b − 2ab − a − 2bc − c + 2bc
= 2b − a − c = 0

Q.148. If the shortest distance between the straight lines 3(x − 1) = 6(y − 2) = 2(z − 1) and 4(x − 2) = 2(y − λ) = (z − 3), λ ∈ R is 1/√38, then the integral value of λ is equal to:          (JEE Main 2021)
(a) 3
(b) 2
(c) 5
(d) −1

Ans. a


Shortest distance = Projection of



⇒ |14 − 5λ| = 1
⇒ 14 − 5λ = 1 or 14 − 5λ = −1
⇒ λ = 13/5 or 3
∴ Integral value of λ = 3. 

Q.149. Let three vectors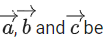such that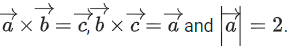Then which one of the following is not true?          (JEE Main 2021)
(a)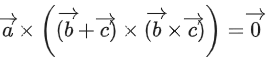
(b)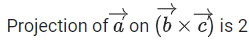
(c)
(d)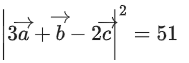

Ans. d





= (9 × 4) + 1 + (4 × 4)
= 36 + 1 + 16 = 53

Q.150. In a triangle ABC, if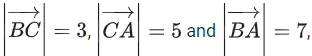then the projection of the vector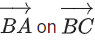is equal to          (JEE Main 2021)
(a) 19/2
(b) 13/2
(c) 11/2
(d) 15/2

Ans. c

Projection of
onis equal to

Q.151. Consider the line L given by the equation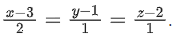Let Q be the mirror image of the point (2, 3, −1) with respect to L. Let a plane P be such that it passes through Q, and the line L is perpendicular to P. Then which of the following points is on the plane P?          (JEE Main 2021)
(a) (−1, 1, 2)
(b) (1, 1, 1)
(c) (1, 1, 2)
(d) (1, 2, 2)

Ans. d
Plane p is ⊥^r to line& passes through pt. (2, 3) equation of plane p
2(x − 2) + 1(y − 3) + 1 (z + 1) = 0
2x + y + z − 6 = 0
Point (1, 2, 2) satisfies above equation

Q.152. The lines x = ay − 1 = z − 2 and x = 3y − 2 = bz − 2, (ab ≠ 0) are coplanar, if:          (JEE Main 2021)
(a) b = 1, a ∈ R − {0}
(b) a = 1, b ∈ R − {0}
(c) a = 2, b = 2
(d) a = 2, b = 3

Ans. a
Lines are x = ay − 1 = z − 2

and x = 3y − 2 = bz − 2

∴ lines are co-planar


⇒ b = 1 and a ∈ R − {0}

Q.153. Let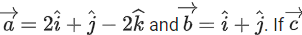is a vector such that 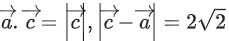and the angle between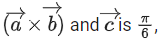then the value of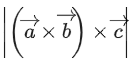is:          (JEE Main 2021)
(a) 2/3
(b) 4
(c) 3
(d) 3/2

Ans. d

⇒ c² + 9 − 2(c) = 8


= (3)(1)(1/2)
= 3/2

Q.154. In a triangle ABC, if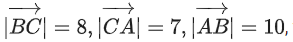then the projection of the vector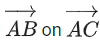is equal to:          (JEE Main 2021)
(a) 25/4
(b) 127/20
(c) 85/14
(d) 115/16

Ans. c

Q.155. Let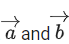be two non-zero vectors perpendicular to each other and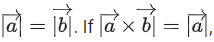then the angle between the vectorsis equal to:          (JEE Main 2021)
(a)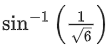
(b)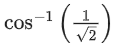
(c)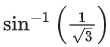
(d)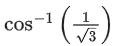

Ans. d









= k² + k² + k²

Q.156. A vector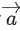has components 3p and 1 with respect to a rectangular cartesian system. This system is rotated through a certain angle about the origin in the counter clockwise sense. If, with respect to new system,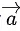has components p + 1 and √10, then the value of p is equal to:          (JEE Main 2021)
(a) 1
(b)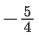
(c) 4/5
(d) -1

Ans. d

(3p)² + 1 = (p + 1)² + 10
⇒ 9p² − p² − 2p − 10 = 0
⇒ 8p² − 2p − 10 = 0
⇒ 4p² − p − 5 = 0
⇒ 4p² − 5p + 4p − 5 = 0
⇒ (4p − 5) (p + 1) = 0
⇒ p = 5/4, − 1

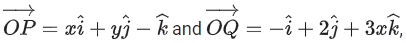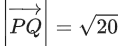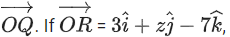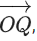Q.157. Let O be the origin. Letx, y ∈ R, x > 0, be such thatand the vectoris perpendicularz ∈ R, is coplanar withandthen the value of x² + y² + z² is equal to:          (JEE Main 2021)
(a) 2
(b) 9
(c) 7
(d) 1

Ans. b


20 = 1 + x² + 2x + 4 + y² − 4y + 9x² + 1 + 6x
20 = 10x² + y² + 8x + 6 − 4y
20 = 10x² + 4x² + 8x + 6 − 8x
14 = 14x² ⇒ x² = 1
Also,
−x + 2y − 3x = 0
4x = 2y
y = 2x
∴ y² = 4x² ⇒ y² = 4
x = 1 as x > 0 and y = 2

⇒ 1(−14 −3z) − 2(7 − 9) − 1(−z −6) = 0
⇒ −14 −3z + 4 + z + 6 = 0
⇒ 2z = −4 ⇒ z = −2
∴ x² + y² + z² = 9

Q.158. If the equation of plane passing through the mirror image of a point (2, 3, 1) with respect to line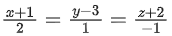and containing the line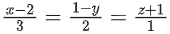is αx + βy + γz = 24, then α + β + γ is equal to:          (JEE Main 2021)
(a) 21
(b) 19
(c) 18
(d) 20

Ans. b

Let point M is (2λ − 1, λ + 3, − λ − 2)
D.R.'s of AM line are < 2λ − 1 − 2, λ + 3 − 3, −λ − 2 − 1>
= < 2λ − 3, λ, −λ −3 >
AM ⊥ line L₁
∴ 2(2λ − 3) + 1(λ) − 1(−λ − 3) = 0

M is mid-point of A & B

B = 2M − A
B ≡ (−2, 4, −6)
Now we have to find equation of plane passing through B(−2, 4, −6) & also containing the line



Point P on line is (2, 1, −1)
of line L₂ is 3, −2, 1


∴ equation of plane is

7x + 11y + z = −14 + 44 −6
7x + 11y + z = 24
∴ α = 7
β = 11
γ = 1
∴ α + β + γ = 19

Q.159. The equation of the plane which contains the y-axis and passes through the point (1, 2, 3) is:          (JEE Main 2021)
(a) x + 3z = 0
(b) 3x − z = 0
(c) x + 3z = 10
(d) 3x + z = 6

Ans. b
Let the equation of the plane is a (x − 1) + b(y − 2) + c(z − 3) = 0
Y-axis lies on it.
D.R.'s of y-axis are 0, 1, 0
∴ 0.a + 1.b + 0.c = 0 ⇒ b = 0
∴ Equation of plane is a(x − 1) + c(z − 3) = 0
x = 0, z = 0 also satisfy it −a −3c = 0 ⇒ a = −3c
−3c (x − 1) + c (z − 3) = 0
−3 + 3 + z − 3 = 0
3x − z = 0 

Q.160. Let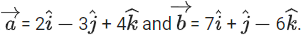
If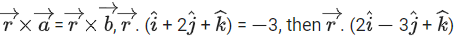is equal to:          (JEE Main 2021)
(a) 10
(b) 8
(c) 13
(d) 12

Ans. d


λ(−5 − 8 + 10) = −3 ⇒ λ = 1
∴ (−5, −4, 10) . (2, −3, 1)
= - 10 + 12 + 10 = 12 

Q.161. If (x, y, z) be an arbitrary point lying on a plane P which passes through the points (42, 0, 0), (0, 42, 0) and (0, 0, 42), then the value of the expression 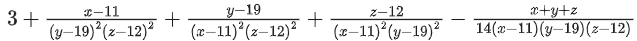is equal to:          (JEE Main 2021)
(a) 3
(b) 39C
(c) −45
(d) 0

Ans. a
From intercept from, equation of plane is x + y + z = 42
⇒ (x − 11) + (y − 19) + (z − 12) = 0
let a = x − 11, b = y − 19, c = z − 12
a + b + c = 0
Now, given expression is

If a + b + c = 0
⇒ a³ + b³ + c³ = 3 abc

= 3

Q.162. If the foot of the perpendicular from point (4, 3, 8) on the line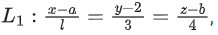l ≠ 0 is (3, 5, 7), then the shortest distance between the line L1 and lineis equal to:          (JEE Main 2021)
(a) 1/√6
(b) 1/2
(c) 1/√3
(d)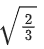

Ans. a
(3, 5, 7) lie on given line L₁

M(4, 3, 8)
N(3, 5, 7)
DR'S of MN = (1, −2, 1)
MN ⊥ line L₁
(1)(l) + (−2)(3) + 4(1) = 0
⇒ l = 2
a = 1
a = 1, b = 3, l = 2

A = <1, 2, 3>
B = <2, 4, 5>

Shortest distance =

Q.163. Let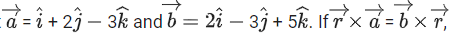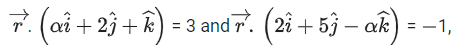α ∈ R, then the value of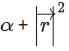is equal to:          (JEE Main 2021)
(a) 13
(b) 11
(c) 9
(d) 15

Ans. d



⇒ λ(6 − 5 − 2α) = −1
λ(1 − 2α) = −1 .... (1)

⇒ λ[3α − 2 + 2] = 3 ⇒ λα = 1 .... (2)
From (1) & (2)

λ − 2 = −1 ⇒ λ = 1α = 1

Q.164. If for a > 0, the feet of perpendiculars from the points A(a, −2a, 3) and B(0, 4, 5) on the plane lx + my + nz = 0 are points C(0, −a, −1) and D respectively, then the length of line segment CD is equal to:          (JEE Main 2021)
(a) √41
(b) √55
(c) √31
(d) √66

Ans. d

Let ϕ is the angle between
CD = AR = | AB |sinϕ


C on plane
(0)l − am − n = 0 ..... (1)


m = −l & an + 4m = 0 ..... (2)
From (1) and (2)
a²m + an = 0

(a² − 4)m = 0 ⇒ a = 2
2m + n = 0 .... (1)
m + l = 0
l² + m² + n² = 1
m² + m² + 4m² = 1
m² = 1/6
m = 1/√6
n = −2/√6
l = −1/√6

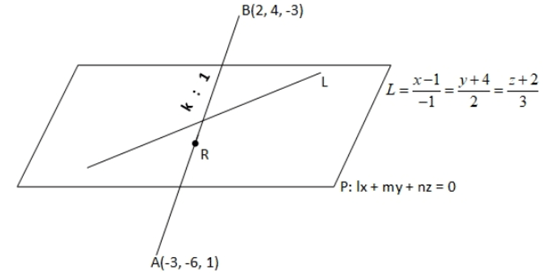
Q.165. Let P be a plane lx + my + nz = 0 containing the line,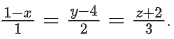If plane P divides the line segment AB joining points A(−3, −6, 1) and B(2, 4, −3) in ratio k : 1 then the value of k is equal to:          (JEE Main 2021)
(a) 2 B
(b) 3
(c) 1.5
(d) 4

Ans. a

Line lies on plane
−l + 2m + 3n = 0 ..... (1)
Point on line (1, −4, −2) lies on plane
l − 4m − 2n = 0 .... (2)
from (1) & (2)
−2m + n = 0 ⇒ 2m = n
l = 3n + 2m ⇒ l = 4n
l : m : n :: 4n : n/2 : n
l : m : n :: 8n : n : 2n
l : m : n :: 8 : 1 : 2
Now equation of plane is 8x + y + 2z = 0
R divide AB is ratio k : 1

−24 + 16k − 6 + 4k + 2 − 6k = 0
−28 + 14k = 0

Q.166. Let the position vectors of two points P and Q be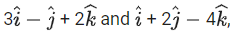 respectively. Let R and S be two points such that the direction ratios of lines PR and QS are (4, −1, 2) and (−2, 1, −2), respectively. Let lines PR and QS intersect at T. If the vector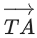is perpendicular to both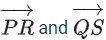and the length of vector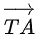is √5 units, then the modulus of a position vector of A is:          (JEE Main 2021)
(a) √171
(b) √227
(c) √482
(d) √5

Ans. a



Now T on PR = ⟨3 + 4λ, −1 − λ, 2 + 2λ⟩
Similarly T on QS = (1 − 2μ, 2 + μ, −4 − 2μ) 

⇒ T : (11, −3, 6) 

Now A = (11, −3 −4λ, 6 − 2λ)
Given, TA = √5
(−3 + 4λ + 3)² + (6 + 2λ − 6)² = 5
16λ² + 4λ² = 5
20λ² = 5 

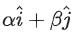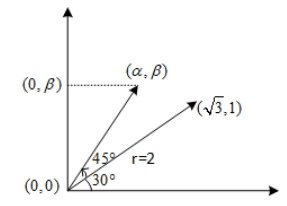
Q.167. Let a vectorbe obtained by rotating the vector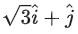by an angle 45^∘ about the origin in counterclockwise direction in the first quadrant. Then the area of triangle having vertices (α, β), (0, β) and (0, 0) is equal to:          (JEE Main 2021)
(a) 1/√2
(b) 1/2
(c) 1
(d) 2√2

Ans. b

(α, β) ≡ (2 cos 75^∘, 2 sin 75^∘)
Area = 12 (2 cos 75^∘) (2 sin 75^∘)
= sin(150^∘) = 1/2 square unit 

Q.168. Let L be a line obtained from the intersection of two planes x + 2y + z = 6 and y + 2z = 4. If point P(α, β, γ) is the foot of perpendicular from (3, 2, 1) on L, then the value of 21(α + β + γ) equals:          (JEE Main 2021)
(a) 102
(b) 142
(c) 136
(d) 68

Ans. a

Dr/s:- (3, −2, 1)
Points on the line (−2, 4, 0)


Dr's of PQ : 3λ−5,−2λ+2,λ−1
Dr's of y lines are (3, −2, 1)
Since PQ⊥ line
3(3λ − 5) − 2(−2λ + 2) + 1(λ − 1) = 0
λ = 10/7

21(α + β + γ) = 21(34/7) = 102

Q.169. If vectors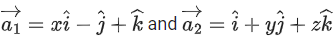are collinear, then a possible unit vector parallel to the vector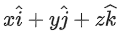is:          (JEE Main 2021)
(a)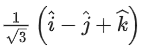
(b)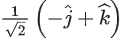
(c)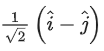
(d)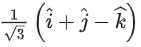

Ans. a

1 = λx, y = −λ, z = λ

Let λ² = 1, possible unit vector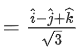 

Q.170. If the mirror image of the point (1, 3, 5) with respect to the plane 4x − 5y + 2z = 8 is (α, β, γ), then 5(α + β + γ) equals:          (JEE Main 2021)
(a) 39
(b) 41
(c) 47
(d) 43

Ans. c
Image of (1, 3, 5) in the plane 4x − 5y + 2z = 8 is (α, β, γ) 

Q.171. If (1, 5, 35), (7, 5, 5), (1, λ, 7) and (2λ, 1, 2) are coplanar, then the sum of all possible values of λ is:          (JEE Main 2021)
(a)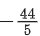
(b)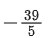
(c) 44/5
(d) 39/5

Ans. c
A(1, 5, 35), B(7, 5, 5), C(1, λ, 7), D(2λ, 1, 2)

Points are coplanar
= 6(−5λ + 25 − 2 + 2λ) − 30(−6 + 6λ − (2λ² − λ − 10λ + 5))
= 6(−3λ + 23) − 30(−2λ² + 11λ − 5 − 6 + 6λ)
= 6(−3λ + 23) − 30(−2λ² + 17λ −11)
= 6(−3λ + 23 + 10λ² − 85λ + 55)
= 6(10λ² − 88λ + 78) = 12(5λ² − 44λ + 39)
⇒ 0 = 12(5λ² − 44λ + 39)
⇒ 5λ² − 44λ + 39 = 0
this quadratic equation has two values λ₁ and λ₂
∴ λ₁ + λ₂ = 44/5

Q.172. Consider the three planes
P₁ : 3x + 15y + 21z = 9,
P₂ : x − 3y − z = 5, and
P₃ : 2x + 10y + 14z = 5
Then, which one of the following is true?          (JEE Main 2021)
(a) P₁ and P₂ are parallel.
(b) P₁, P₂ and P₃ all are parallel.
(c) P₁ and P₃ are parallel.
(d) P₂ and P₃ are parallel.

Ans. c
P₁ : 3x + 15y + 21z = 9,
P₂ : x − 3y − z = 5
P₃ : x + 5y + 7z = 5/2
∴ P₁ and P₃ are parallel. 

Q.173. If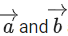are perpendicular, thenis equal to:          (JEE Main 2021)
(a)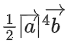
(b)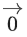
(c)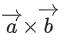
(d)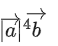

Ans. d

Q.174. A plane passes through the points A(1, 2, 3), B(2, 3, 1) and C(2, 4, 2). If O is the origin and P is (2, −1, 1), then the projection of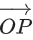on this plane is of length:          (JEE Main 2021)
(a)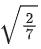
(b)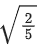
(c)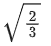
(d)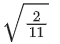

Ans. d
A(1, 2, 3), B(2, 3, 1), C(2, 4, 2), O(0, 0, 0)
Equation of plane passing through A, B, C will be

⇒ (x − 1)(−1 + 4) − (y − 2)(−1 + 2) + (z − 3)(2 − 1) = 0
⇒ (x − 1)(3) − (y − 2)(1) + (z − 3)(1) = 0
⇒ 3x − 3 − y + 2 + z − 3 = 0
⇒ 3x − y + z − 4 = 0, is the required plane.
Now, O(0, 0, 0) & P(2, −1, 1)

Plane is 3x − y + z − 4 = 0
O' & P' are foot of perpendiculars.
For O' 

for P' 

Q.175. Let α be the angle between the lines whose direction cosines satisfy the equations l + m − n = 0 and l² + m² − n² = 0. Then the value of sin⁴α + cos⁴α is:          (JEE Main 2021)
(a) 3/8
(b) 3/4
(c) 1/2
(d) 5/8

Ans. d
l² + m² + n² = 1
∴ 2n² = 1 (∵ l² + m² − n² = 0)

⇒ lm = 0 or m = 0

Q.176. The equation of the line through the point (0, 1, 2) and perpendicular to the line

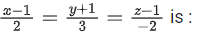         (JEE Main 2021)
(a)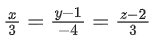
(b)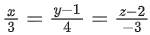
(c)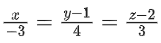
(d)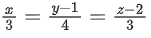

Ans. c

Any point on this line (2λ + 1, 3λ − 1, −2λ + 1)

Direction ratio of given line (2, 3, −2)
Direction ratio of line to be found (2λ + 1, 3λ − 2, −2λ − 1)

⇒ λ = 2/17
Direction ratio of line (21, −28, −21) ≡ (3, −4, −3) ≡ (−3, 4, 3)  

Q.177. The vector equation of the plane passing through the intersection of the planes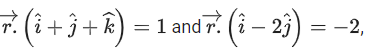and the point (1, 0, 2) is:         (JEE Main 2021)
(a)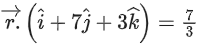
(b)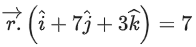
(c)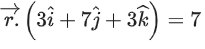
(d)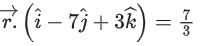

Ans. b
Given, point (1, 0, 2)
Equation of plane = 

Equation of plane passing through the intersection of given planes is

∴ This plane passes through point (1, 0, 2) i.e., 


⇒ (3 − 1) + λ(1 + 2) = 0
⇒ 2 + λ × 3 = 0
⇒ λ = −2/3
Hence, equation of required plane is 

Q.178. Let a, b ∈ R. If the mirror image of the point P(a, 6, 9) with respect to the line 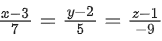is (20, b, −a−9), then | a + b |, is equal to:         (JEE Main 2021)
(a) 88
(b) 90
(c) 86
(d) 84

Ans. a
Given, P(a, 6, 9)
Equation of line
Image of point P with respect to line is point Q(20, b, −a −9)
Mid-point of P and Q =
This point lies on line 

Solving, we get a = − 56, b = − 32
∴ |a + b| = |−56 − 32| = 88

Q.179. The distance of the point (1, 1, 9) from the point of intersection of the line 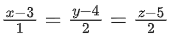and the plane x + y + z = 17 is:         (JEE Main 2021)
(a) 19√2
(b) 2√19
(c) 38
(d) √38

Ans. d
Given, P(1, 1, 9).
Equation of plane x + y + z = 17
Equation of line

⇒ x = λ + 3; y = 2λ + 4; z = 2λ + 5
∴ The point we have is (λ + 3, 2λ + 4, 2λ + 5).
∵ This point lies on the plane x + y + z = 17.
∴ λ + 3 + 2λ + 4 + 2λ + 5 = 17
⇒ λ = 1
∴ The coordinate of point is (4, 6, 7)
∴ Required distance between (1, 1, 9) and (4, 6, 7) is 

Q.180. The equation of the plane passing through the point (1, 2, -3) and perpendicular to the planes 3x + y - 2z = 5 and 2x - 5y - z = 7, is:         (JEE Main 2021)
(a) 6x - 5y + 2z + 10 = 0
(b) 3x - 10y - 2z + 11 = 0
(c) 6x - 5y - 2z - 2 = 0
(d) 11x + y + 17z + 38 = 0

Ans. d
Given, equation of planes are
3x + y - 2z = 5
2x - 5y - z = 7
and point ( 1, 2, 3).
Normal vector of required plane = 


Now, the equation of plane passing through (1, 2, -3) having normal vectoris
-[11(x - 1) + (y - 2) + 17(z + 3)] = 0
⇒ 11x + y + 17z + 38 = 0