Short Notes: Unsymmetrical Faults | Power Systems - Electrical Engineering (EE) PDF Download
Introduction
The types of faults occurring in power systems are symmetrical and unsymmetrical faults. The unsymmetrical fault is the type of fault in which the three-phase line of the system becomes unbalanced therefore giving rise to unbalanced currents in the different phases.
In brief the types of unsymmetrical faults we will be discussing are:
- Single line-to-ground fault (SLG)
- Line-to-line fault (L-L)
- Double line-to-ground fault (2LG)
- Balanced three-phase fault
These faults give rise to unsymmetrical currents therefore different fault currents flow in different phases.
Here we will be discussing the types of unsymmetrical faults concerning a synchronous generator operating at no load.
Types of Unsymmetrical Faults
Following are the types of unsymmetrical faults in the power system.
Balanced Three-Phase Unsymmetrical Faults
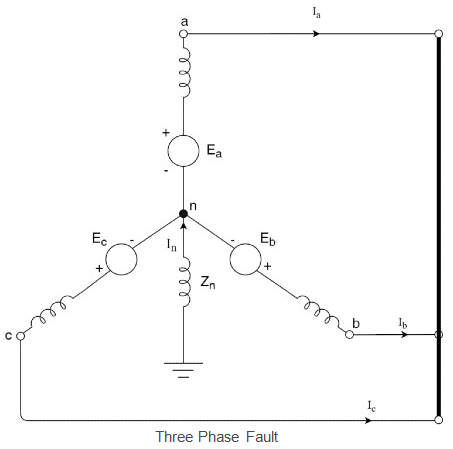
In balanced three-phase unsymmetrical faults, the fault occurs when all the three phases of the transmission line or the terminals of the machine come in contact with each other.
Here let us consider an unloaded three-phase star-connected alternator. There is balanced three-phase unsymmetrical faults occurring at the terminals of the generator as a result the phase currents (Ia, Ib, and Ic) and voltages to be zero.
Firstly here,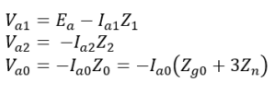
Where Zn is the impedance through which generator neutral is earthed.
Secondly, representing above relations in matrix form
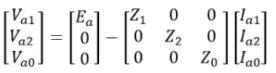
Further from the above matrix form we have, Finally, we have,
Finally, we have,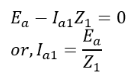 In the case of balanced three-phase unsymmetrical faults, only the positive sequence network is present in the solution.
In the case of balanced three-phase unsymmetrical faults, only the positive sequence network is present in the solution.
Single Line-To-Ground Fault (L-G)
For single line-to-ground unsymmetrical faults, we consider a synchronous generator where a fault occurs at the ‘a’ phase of the generator with the fault impedance of Zf.
The generator is grounded through an impedance of Zn.
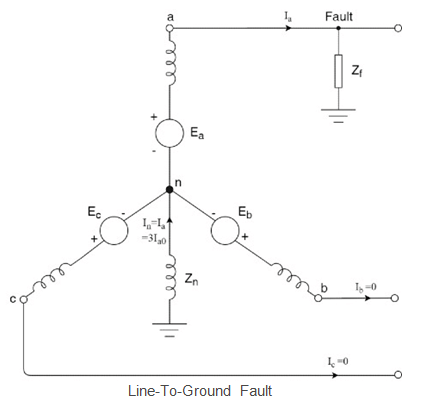
Under the single line-to-ground unsymmetrical faults condition, firstly we have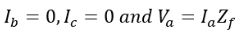 Here we use the symmetrical components and represent the fault currents by substituting the above values. As Ib=0 and Ic=0.
Here we use the symmetrical components and represent the fault currents by substituting the above values. As Ib=0 and Ic=0.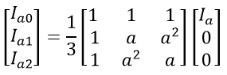 Secondly, from the above equation
Secondly, from the above equation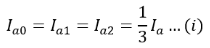 Further, we have,
Further, we have,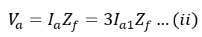 From the sequence network of a synchronous generator, we have the positive, negative, and zero sequence voltages as,
From the sequence network of a synchronous generator, we have the positive, negative, and zero sequence voltages as,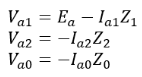 Moreover, substituting the value of equations (i) and (ii) in the above equations we have
Moreover, substituting the value of equations (i) and (ii) in the above equations we have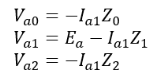 Also, we know that
Also, we know that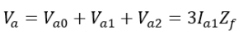 So,
So,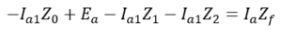 Therefore we have the expression of current as,
Therefore we have the expression of current as,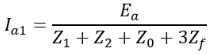 Finally, the figure below shows the sequence networks representing the L-G fault.
Finally, the figure below shows the sequence networks representing the L-G fault.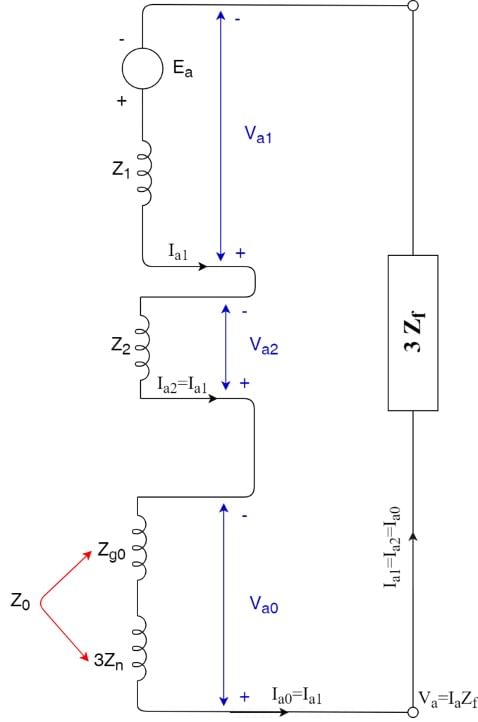
Line-To-Line Fault (L-L)
For line-to-line unsymmetrical faults, we consider a synchronous generator where a line-to-line fault occurs on the phases ‘b’ and ‘c’ with a fault impedance of Zf.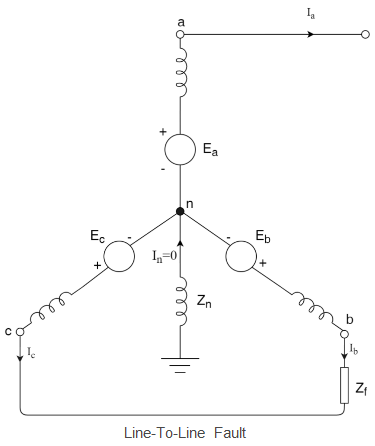
Firstly, under the condition of line-to-line fault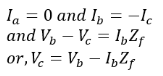 Here we use the symmetrical components and represent the fault currents by substituting the above values.
Here we use the symmetrical components and represent the fault currents by substituting the above values.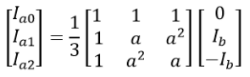 Secondly, from this relation we have
Secondly, from this relation we have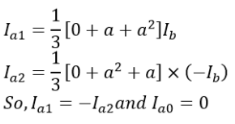 Similarly, representing the voltages in terms of symmetrical components.
Similarly, representing the voltages in terms of symmetrical components. Further from this equation we have,
Further from this equation we have,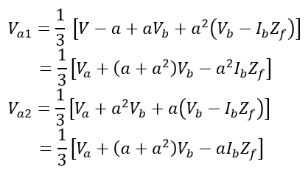 Solving the above two equations for Va1 and Va2.
Solving the above two equations for Va1 and Va2.
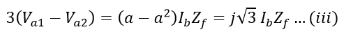 As Ia2 = – Ia1 and Ia =0 so,
As Ia2 = – Ia1 and Ia =0 so,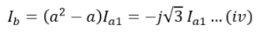 Moreover from equation (iii) and (iv), we have
Moreover from equation (iii) and (iv), we have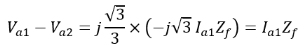 Finally, the figure below shows the sequence network of L-L fault occurring on phases b and c of the generator.
Finally, the figure below shows the sequence network of L-L fault occurring on phases b and c of the generator.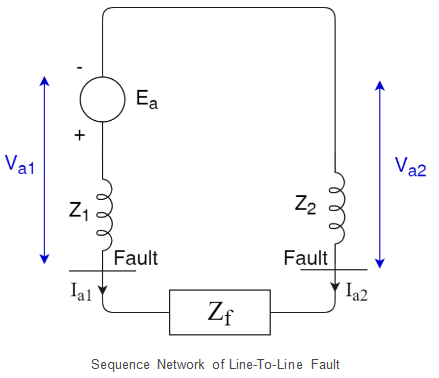 In the terms of Thevenin’s equivalent circuit, the currents are
In the terms of Thevenin’s equivalent circuit, the currents are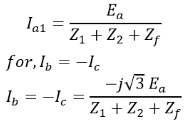
Double Line-to-Ground Fault (L-L-G)
Here, we consider a synchronous generator where a double line-to-ground fault occurs between phases ‘b’, ‘c’, and ground with a fault impedance of Zf.
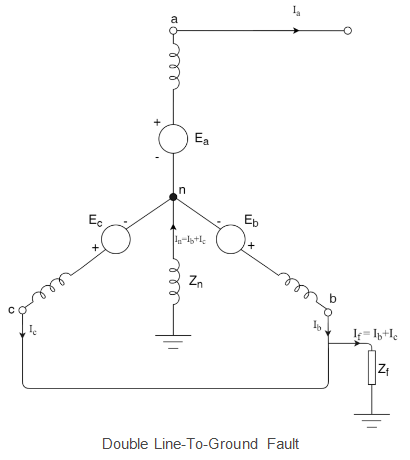 Under the condition of fault
Under the condition of fault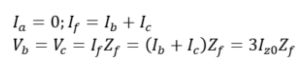 The symmetrical components of voltages are
The symmetrical components of voltages are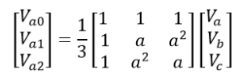 From the above equation
From the above equation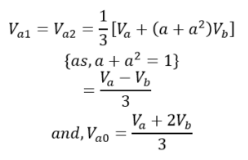 Now, subtracting Va1 from Va0.
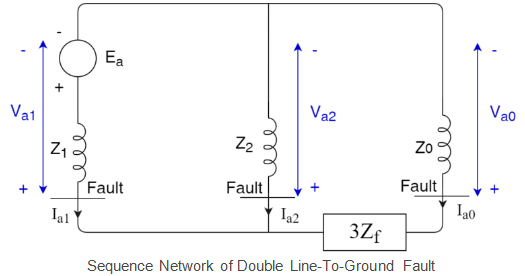
Now, subtracting Va1 from Va0.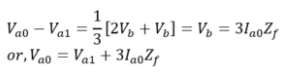 The figure below shows the sequence network of the double line-to-line fault of the generator.
The figure below shows the sequence network of the double line-to-line fault of the generator.
In the terms of Thevenin’s equivalent circuit, the currents are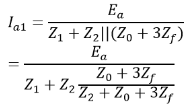 In the cases of direct short-circuit for all the above fault cases, take Zf =0.
In the cases of direct short-circuit for all the above fault cases, take Zf =0.
|
30 videos|101 docs|45 tests
|





















