Overhead Insulators & Underground Cables - 2 | Power Systems - Electrical Engineering (EE) PDF Download
Classification of Cables
Cables for underground service may be classified in two ways according to (i) the type of insulating material used in their manufacture (ii) the voltage for which they are manufactured. However, the latter method of classification is generally preferred, according to which cables can be divided into the following groups:
- Low-tension (L.T.) cables — up to 1000 V
- High-tension (H.T.) cables — up to 11,000V
- Super-tension (S.T.) cables — from 22 kV to 33 kV
- Extra high-tension (E.H.T.) cables — from 33 kV to 66 kV
- Extra super voltage cables — beyond 132 kV
A cable may have one or more than one core depending upon the type of service for which it is
intended. It may be (i) single-core (ii) two-core (iii) three-core (iv) four-core etc. For a 3-phase service, either 3-single-core cablesorthree-core cable can be used depending upon the operating voltage and load demand. Figure shows the constructional details of a single-core low tension cable. The cable has ordinary construction be- cause the stresses developed in the cable for low voltages(up to 6600 V) are generally small. It consists of one circular core of tinned stranded copper (or aluminium) insulated by layers of impregnated paper. The insulation is surrounded by a lead sheath which prevents the entry of moisture into the inner parts. In order to protect the lead sheath from corrosion, an overall serving of compounded fibrous material (jute etc.) is provided. Single-core cables are not usually armouredin order to avoid excessive sheath losses. The principal advantages of single-core cables are simple construction and availability of larger copper section.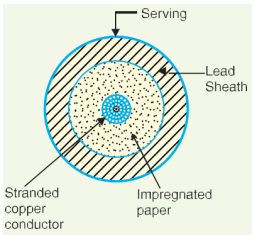
Cables for 3-Phase Service
- In practice, underground cables are generally required to deliver 3-phase power. For the purpose, either three-core cable or *three single core cables may be used. For voltages up to 66 kV, 3-core cable (i.e., multi-core construction) is preferred due to economic reasons. However, for voltages beyond 66 kV, 3-corecables become too large and unwieldy and, therefore, single-core cables are used. The following types of cables are generally used for 3-phase service:
1. Belted cables: These cables are used for voltages upto 11kV but in extraordinary cases, their use may be extended upto 22kV. Fig. 11.3 shows the constructional details of a 3-core belted cable. The cores are insulated from each other by layers of impregnated paper. Another layer of impreg- nated paper tape, called paper belt is wound round the grouped insulated cores. The gap between the insulated coresis filled with fibrousinsulating material (jute etc.) so as to give circular cross-section to the cable. The cores are generally stranded and may be of non- circular shape to make better use of available space. The belt is covered with lead sheath to protect the cable against ingress of moisture and mechanical injury. The lead sheath is covered with one or more layers of armouring with an outer serving (not shown in the fig- ure). The belted type construction is suitable only for low and medium voltages as the electrostatic stresses developed in the cables for these voltages are more or less radial i.e., across the insulation. However, for high voltages (beyond 22 kV), the tangential stresses also become important. These stresses act along the layers of paper insulation. As the insulation resistance of paper is quitesmall along the layers, therefore, tangential stresses set up **leakage current along the layers of paper insulation. The leakage current causes local heating, resulting in the risk of breakdown of insulation at any moment. In order to overcome this difficulty, screened cables are used where leakage currents are conducted to earth through metallic screens.
2. Screened cables: These cables are meant for use up to 33 kV, but in particular cases their use may be extended to operating voltages up to 66 kV. Two principal types of screened cables are H- type cables and S.L. type cables.
- H-type cables: This type of cable was first designed by H. Hochstadter and hence the name. Figure shows the constructional details of a typical 3-core, H-type cable. Each core is insulated by layers of impregnated paper. The insulation on each core is covered with ametallic screen which usually consists of a perforated aluminium foil. The cores are laid in such a way that metallic screens make contact with one another. An additional conducting belt (copper woven fabric tape) is wrapped round the three cores. The cable has no insulating belt but lead sheath, bedding, armouring and serving follow as usual. It is easy to see that each core screen is in electrical con- tact with the conducting belt and the lead sheath. As all the four screens (3 core screens and one conducting belt) and the lead sheath are at †earth potential, therefore, the electrical stresses are purely radial and consequently dielectric losses are reduced.
- Two principal advantages are claimed for H-type cables. Firstly, the perforations in the metallic screens assist in the complete impregnation of the cable with the compound and thus the possibility of air pockets or voids (vacuous spaces) in the dielectric is eliminated. The voids if present tend to reduce the breakdown strength of the cable and may cause considerable damage to the paper insulation. Secondly, the metallic screens increase the heat dissipating power of the cable.
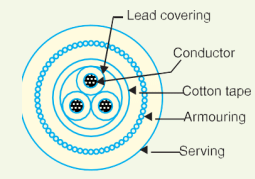
- S.L. type cables: Figure shows the constructional details of a 3-core *S.L. (separate lead) type cable. It is basically H-type cable but the screen round each core insulation is covered by its own lead sheath. There is no overall lead sheath but only armouring and serving are provided. The S.L. type cables have two main advantages over H-type cables. Firstly, the separate sheaths minimize the possibility of core-to-core breakdown. Secondly, bending of cables becomes easy due to the elimination of overall lead sheath. However, the disadvantage is that the three lead sheaths of S.L. cable are much thinner than the single sheath of H-cable and, therefore, call for greater care in manufacture.
Limitations of solid type cables:
All the cables of above construction are referred to as solid type cables because solid insulation is used and no gas or oil circulates in the cable sheath. The voltage limit for solid type cables is 66 kV due to the following reasons:
- As a solid cable carries the load, its conductor temperature increases and the cable compound (i.e., insulating compound over paper) expands. This action stretches the lead sheath which may be damaged.
- When the load on the cable decreases, the conductor cools and a partial vacuum is formed within the cable sheath. If the pinholes are present in the lead sheath, moist air may be drawn into the cable. The moisture reduces the dielectric strength of insulation and may eventually cause the break- down of the cable.
- In practice, †voids are always present in the insulation of a cable. Modern techniques of manufacturing have resulted in void free cables. However, under operating conditions, the voids are formed as a result of the differential expansion and contraction of the sheath and impregnated compound. The breakdown strength of voids is considerably less than that of the insulation. If the void is small enough, the electrostatic stress across it may cause its breakdown. The voids nearest to the conductor are the first to break down, the chemical and thermal effects of ionization causing permanent damage to the paperinsulation.
3. Pressure cables: For voltages beyond 66 kV, solid type cables are unreliable because there is a danger of breakdown of insulation due to the presence of voids. When the operating voltages are greater than 66 kV, pressure cables are used. In such cables, voids are eliminated by increasing the pressure of compound and for this reason they are called pressure cables. Two types of pressure cables viz oil-filled cables and gas pressure cables are commonly used.
- Oil-filled cables. In such types of cables, channels or ducts are provided in the cable for oil circulation. The oil under pressure (it is the same oil used for impregnation) is kept constantly supplied to the channel by means of external reservoirs placed at suitable distances (say 500 m) along the route of the cable. Oil under pressure compresses the layers of paper insulation and is forced into any voids that may have formed between the layers. Due to the elimination of voids, oil-filled cables can be used for higher voltages, the range being from 66 kV up to 230 kV. Oil-filled cables are of three types viz., single-core conductor channel, single-core sheath channel and three-core filler-space channels. Figure shows the constructional details of a single-core conductor channel, oil filled cable.
- The oil channel is formed at the centre by stranding the conductor wire around a hollow cylindrical steel spiral tape. The oil under pressure is supplied to the channel by means of external reservoir. As the channel ismade of spiral steel tape, it allows the oil to percolate between copper strands to the wrapped insulation. The oil pressure compresses the layers of paper insulation and prevents the possibility of void formation. The system is so designed that when the oil gets expanded due to increase in cable temperature, the extra oil collects in the reservoir. How- ever, when the cable temperature falls during light load conditions, the oil from the reservoir flows to the channel. The disadvantage of this type of cable is that the channel is at the middle of the cable and is at full voltage w.r.t. earth, so that a very complicated system of joints is necessary. Figure shows the constructional details of a single- core sheath channel oil-filled cable. In this type of cable, the conductor is solid similar to that of solid cable and is paper insulated. However, oil ducts are provided in the metallic sheath asshown. In the 3-core oil-filler cable shown
Dielectric stress in cable
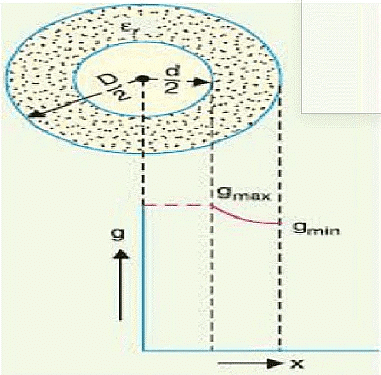 Under operating conditions, the insulation of a cable is subjected to electrostatic forces. This is known as dielectric stress. The dielectric stress at any point in a cable is in fact the potential gradient (or electric intensity) at that point. Consider a single core cable with core diameter d and internal sheath diameter D. The electric intensity at a point x meters from the centre of the cable is
Under operating conditions, the insulation of a cable is subjected to electrostatic forces. This is known as dielectric stress. The dielectric stress at any point in a cable is in fact the potential gradient (or electric intensity) at that point. Consider a single core cable with core diameter d and internal sheath diameter D. The electric intensity at a point x meters from the centre of the cable is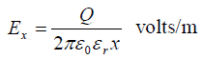 By definition, electric intensity is equal to potential gradient. Therefore, potential gradient g at a point x meters from the Centre of cable is
By definition, electric intensity is equal to potential gradient. Therefore, potential gradient g at a point x meters from the Centre of cable is Potential difference V between conductor and sheath is
Potential difference V between conductor and sheath is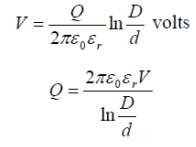 Substituting the value of Q, we get
Substituting the value of Q, we get It is clear from the above equation that potential gradient varies inversely as the distance x. Therefore, potential gradient will be maximum when x is minimum i.e., when x = d/2 or at the surface of the conductor. On the other hand, potential gradient will be minimum at x = D/2 or at sheath surface. Maximum potential gradient is Minimum potential gradient is The variation of stress in the dielectric is shown in Figure. It is clear that dielectric stress is maximum at the conductor surface and its value goes on decreasing as we move away from the conductor. It may be noted that maximum stress is an important consideration in the design of a cable. For instance, if a cable is to be operated at such a voltage that maximum stress is 5 kV/mm, then the insulation used must have a dielectric strength of at least 5 kV/mm, otherwise breakdown of the cable will become inevitable.
It is clear from the above equation that potential gradient varies inversely as the distance x. Therefore, potential gradient will be maximum when x is minimum i.e., when x = d/2 or at the surface of the conductor. On the other hand, potential gradient will be minimum at x = D/2 or at sheath surface. Maximum potential gradient is Minimum potential gradient is The variation of stress in the dielectric is shown in Figure. It is clear that dielectric stress is maximum at the conductor surface and its value goes on decreasing as we move away from the conductor. It may be noted that maximum stress is an important consideration in the design of a cable. For instance, if a cable is to be operated at such a voltage that maximum stress is 5 kV/mm, then the insulation used must have a dielectric strength of at least 5 kV/mm, otherwise breakdown of the cable will become inevitable.
Most Economical Conductor
It has already been shown that maximum stress in a cable occurs at the surface of the conductor. For safe working of the cable, dielectric strength of the insulation should be more than the maximums tress. Rewriting the expression for maximum stress, we get,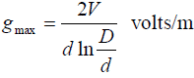 The values of working voltage V and internal sheath diameter D have to be kept fixed at certain values due to design considerations. This leaves conductor diameter d to be the only variable. For given values of V and D, the most economical conductor diameter will be one for which gmax has a minimum value. The value of gmax will be minimum when dln D/d is maximum i.e.
The values of working voltage V and internal sheath diameter D have to be kept fixed at certain values due to design considerations. This leaves conductor diameter d to be the only variable. For given values of V and D, the most economical conductor diameter will be one for which gmax has a minimum value. The value of gmax will be minimum when dln D/d is maximum i.e.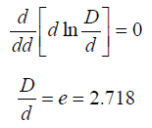 Most economical conductor diameter is
Most economical conductor diameter is
d = D/2.718
And the value of gmax under this condition is
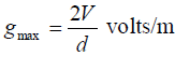 Grading of cables
Grading of cables
- The process of achieving uniform electrostatic stress in the dielectric of cables is known as grading of cables. It has already been shown that electrostatic stress in a single core cable has a maximum value (gmax) at the conductor surface and goes on decreasing as we move towards the sheath. The maximum voltage that can be safely applied to a cable depends upon gmax i.e., electrostatic stress at the conductor surface. For safe working of a cable having homogeneous dielectric, the strength of dielectric must be more than gmax. If a dielectric of high strength is used for a cable, it is useful only near the conductor where stress is maximum. But as we move away from the conductor, the electrostatic stress decreases, so the dielectric will be unnecessarily over strong. The unequal stress distribution in a cable is undesirable for two reasons. Firstly, insulation of greater thickness is required which increases the cable size.
- Secondly, it may lead to the breakdown of insulation. In order to overcome above disadvantages, it is necessary to have a uniform stress distribution in cables. This can be achieved by distributing the stress in such a way that its value is increased in the outer layers of dielectric. This is known as grading of cables.
The following are the two main methods of grading of cables:
- Capacitance Grading: The process of achieving uniformity in the dielectric stress by using layers of different dielectrics is known as capacitance grading. In capacitance grading, the homogeneous dielectric is replaced by a composite dielectric. The composite dielectric consists of various layers of different dielectrics in such a manner that relative permittivity > r of any layer is inversely proportional to its distance from the center. Under such conditions, the value of potential gradient any point in the dielectric is constant and is independent of its distance from the center. In other words, the dielectric stress in the cable is same everywhere and the grading is ideal one. However, ideal grading requires the use of an infinite number of dielectrics which is an impossible task. In practice, two or three dielectrics are used in the decreasing order of permittivity, the dielectric of highest permittivity being used near the core. The capacitance grading can be explained beautifully by referring to the above Figure. There are three dielectrics of outer diameter d1, d2 and D and of relative permittivity >1, >2 and >3 respectively. If the permittivity are such that >1 > 2 > 3 and the three dielectrics are worked at the same maximum stress, then
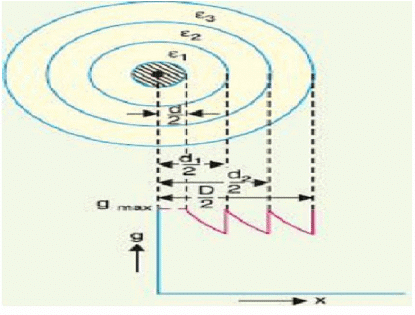
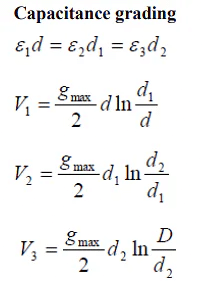 Total p.d. between core and earthed sheath is
Total p.d. between core and earthed sheath is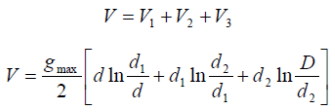
Intersheath Grading: In this method of cable grading, a homogeneous dielectric is used, but it is divided into various layers by placing metallic inters heaths between the core and lead sheath. The inter sheaths are held at suitable potentials which are in between the core potential and earth potential. This arrangement improves voltage distribution in the dielectric of the cable and consequently more uniform potential gradient is obtained.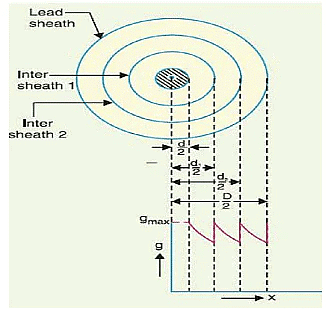 Consider a cable of core diameter d and outer lead sheath of diameter D. Suppose that two intersheaths of diameters d1 and d2 are inserted into the homogeneous dielectric and maintained at some fixed potentials. Let V1, V2 and V3 respectively be the voltage between core and Intersheath 1, between inter sheath 1 and 2 and between inter sheath 2 and outer lead sheath. As there is a definite potential difference between the inner and outer layers of each inter sheath, therefore, each sheath can be treated like a homogeneous single core cable Maximum stress between core and inter sheath 1 is
Consider a cable of core diameter d and outer lead sheath of diameter D. Suppose that two intersheaths of diameters d1 and d2 are inserted into the homogeneous dielectric and maintained at some fixed potentials. Let V1, V2 and V3 respectively be the voltage between core and Intersheath 1, between inter sheath 1 and 2 and between inter sheath 2 and outer lead sheath. As there is a definite potential difference between the inner and outer layers of each inter sheath, therefore, each sheath can be treated like a homogeneous single core cable Maximum stress between core and inter sheath 1 is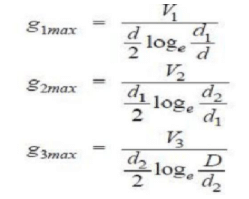
Since the dielectric is homogeneous, the maximum stress in each layer is the same i.e.,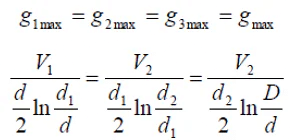 As the cable behaves like three capacitors in series, therefore, all the potentials are in phase i.e. Voltage between conductor and earthed lead sheath is
As the cable behaves like three capacitors in series, therefore, all the potentials are in phase i.e. Voltage between conductor and earthed lead sheath is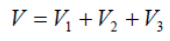 Inter sheath grading has three principal disadvantages. Firstly, there are complications in fixing the sheath potentials. Secondly, the inter sheaths are likely to be damaged during transportation and installation which might result in local concentrations of potential gradient. Thirdly, there are considerable losses in the inter sheaths due to charging currents. For these reasons, inter sheath grading is rarely used.
Inter sheath grading has three principal disadvantages. Firstly, there are complications in fixing the sheath potentials. Secondly, the inter sheaths are likely to be damaged during transportation and installation which might result in local concentrations of potential gradient. Thirdly, there are considerable losses in the inter sheaths due to charging currents. For these reasons, inter sheath grading is rarely used.
Measurements capacitance of 3-core cables
In three-core cables, capacitance does not have a single value, but can be lumped as shown in below figure.
Capacitance between each core and sheath = CS
Capacitance between cores = C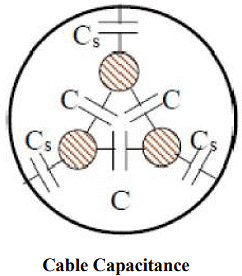 These can be separated from measurements as described in the following section.
These can be separated from measurements as described in the following section.
(a) Strap the 3 cores together and measure the capacitance between this bundle and the sheath as shown in figure.
Measured value = Cm1 = 3 Cs
This gives the capacitance to the sheath as Cs =CMI/3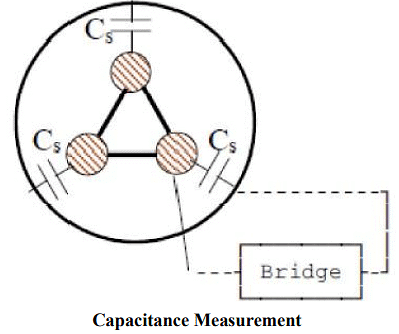 (b) Connect 2 of the cores to the sheath and measure between the remaining core and the sheath.
(b) Connect 2 of the cores to the sheath and measure between the remaining core and the sheath.
Measured value Cm2= 2 C + Cs
i.e. C = (Cm2 – Cs)/2 = (3 Cm2 – Cm1)/6
Which gives the capacitance between the conductors.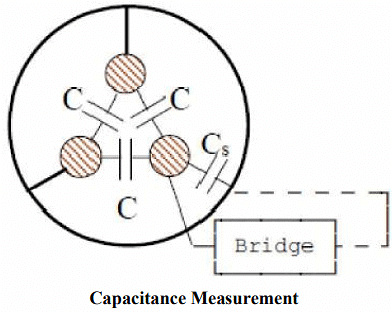
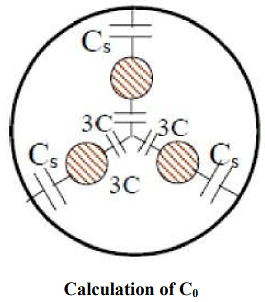
The effective capacitance to neutral Co of any of the cores may be obtained by considering the star equivalent. This gives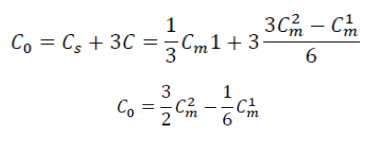
 In the breakdown of actual 3-core belted cables, it is generally observed that charring occurs at those places where the stress is tangential to the layers of paper. Thus for the insulation to be effective, the tangential stresses in paper insulation should be preferably avoided. This can usually be accomplished only screening each core separately (or by having individual lead sheaths for each of the cores), so that the cable in effect becomes 3 individual cables laid within the same protective covering.
In the breakdown of actual 3-core belted cables, it is generally observed that charring occurs at those places where the stress is tangential to the layers of paper. Thus for the insulation to be effective, the tangential stresses in paper insulation should be preferably avoided. This can usually be accomplished only screening each core separately (or by having individual lead sheaths for each of the cores), so that the cable in effect becomes 3 individual cables laid within the same protective covering.
|
21 videos|109 docs|45 tests
|
















