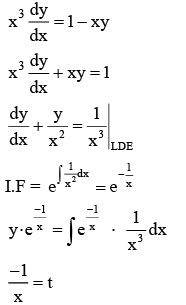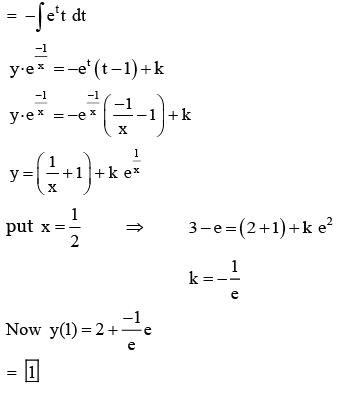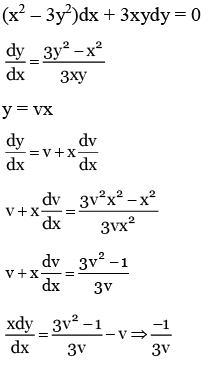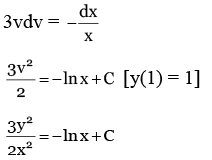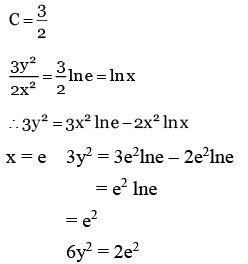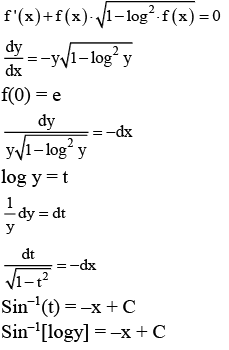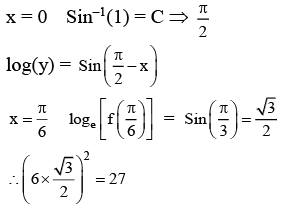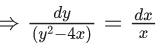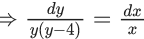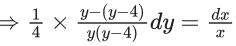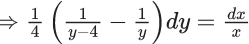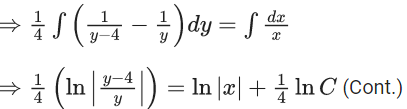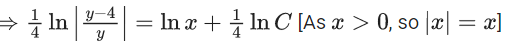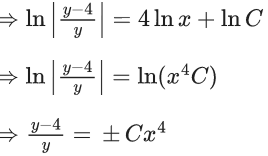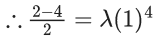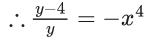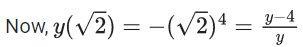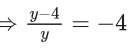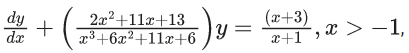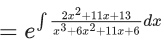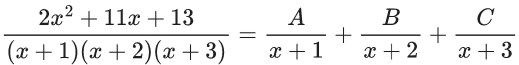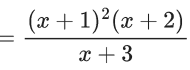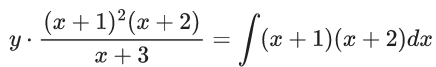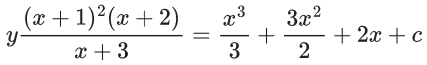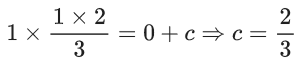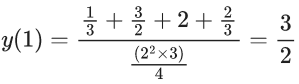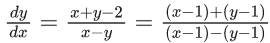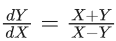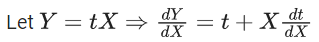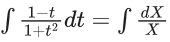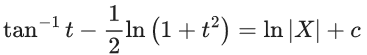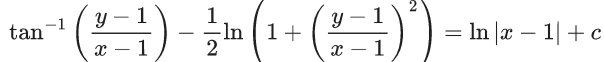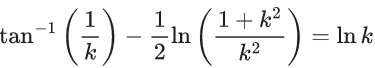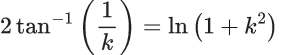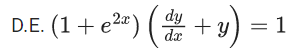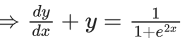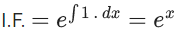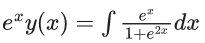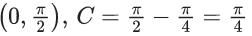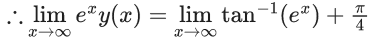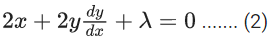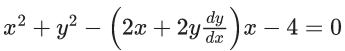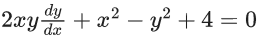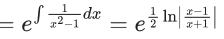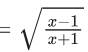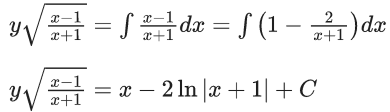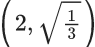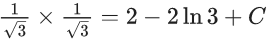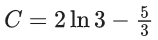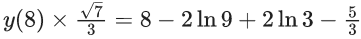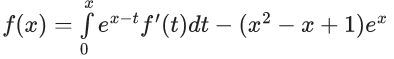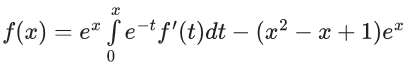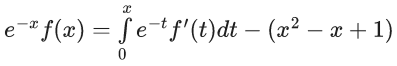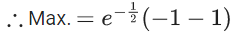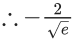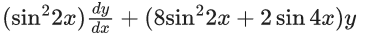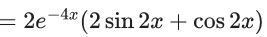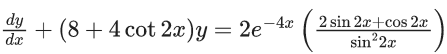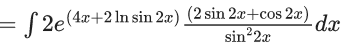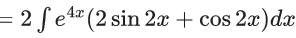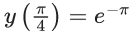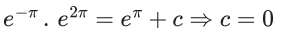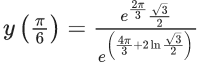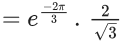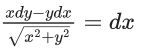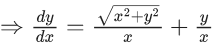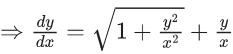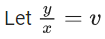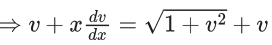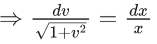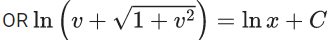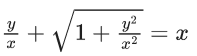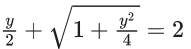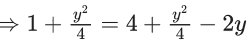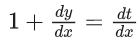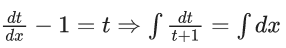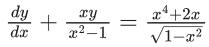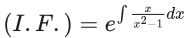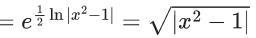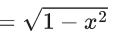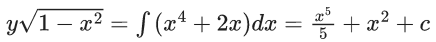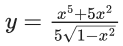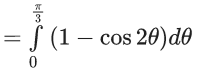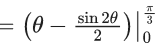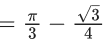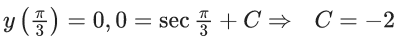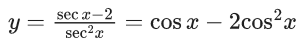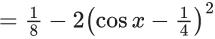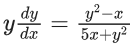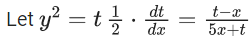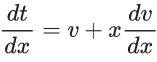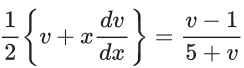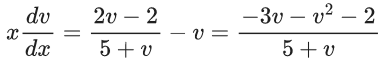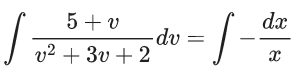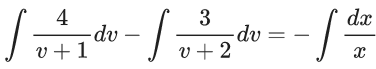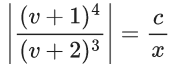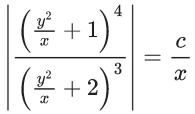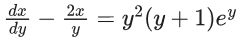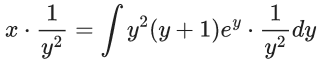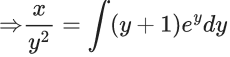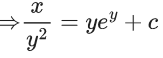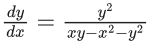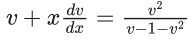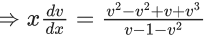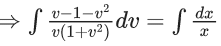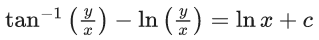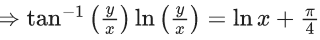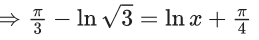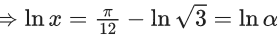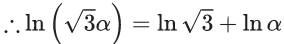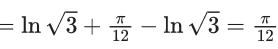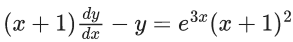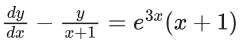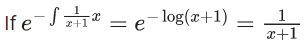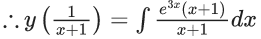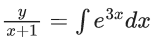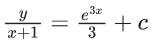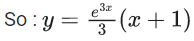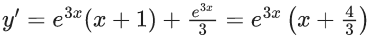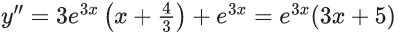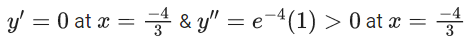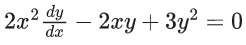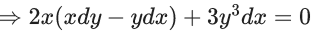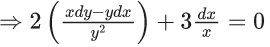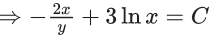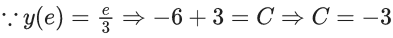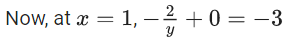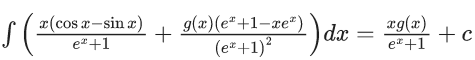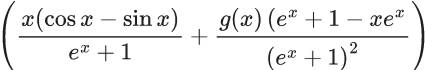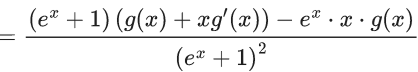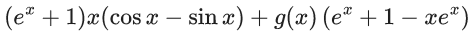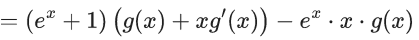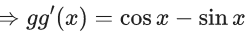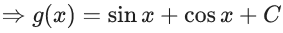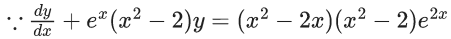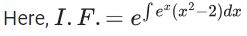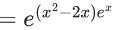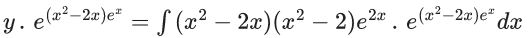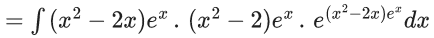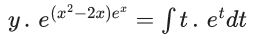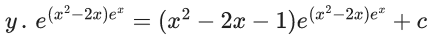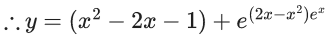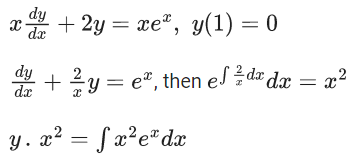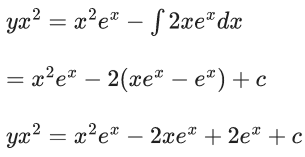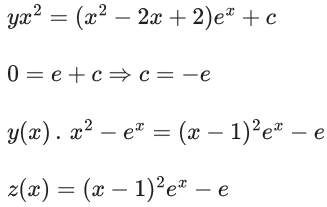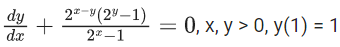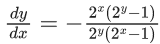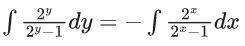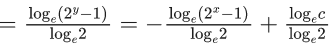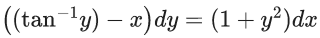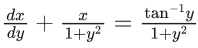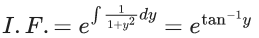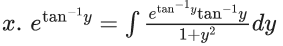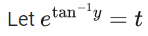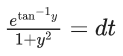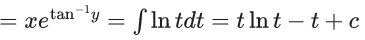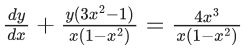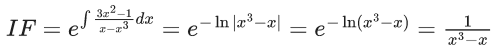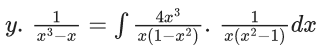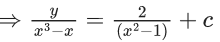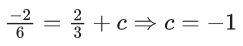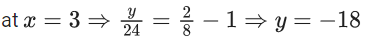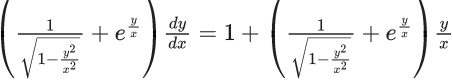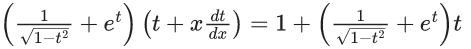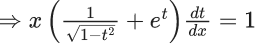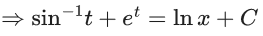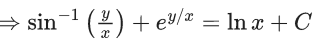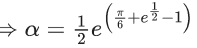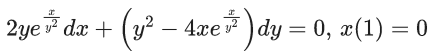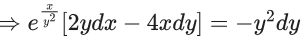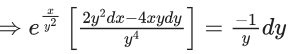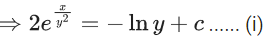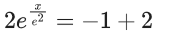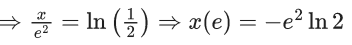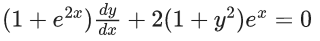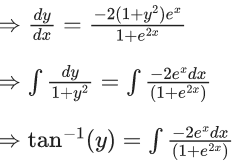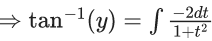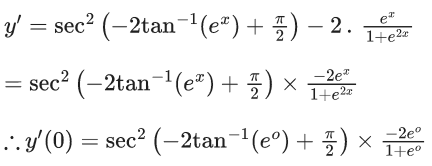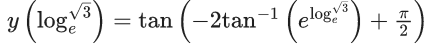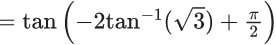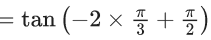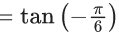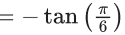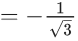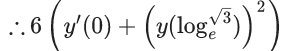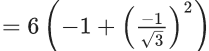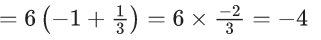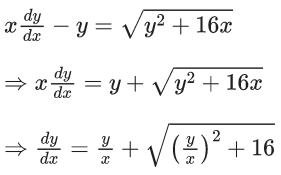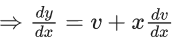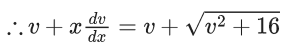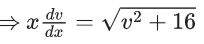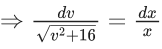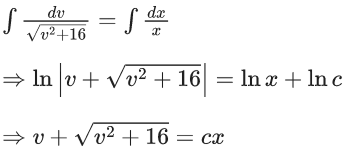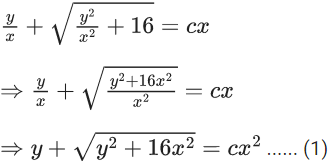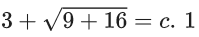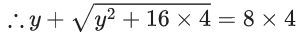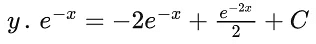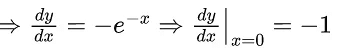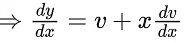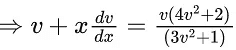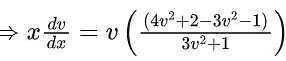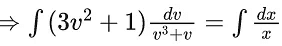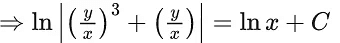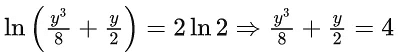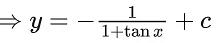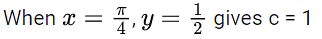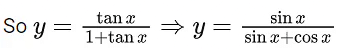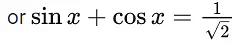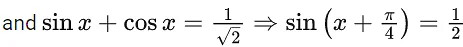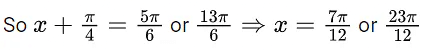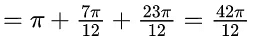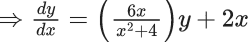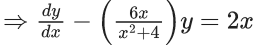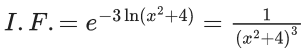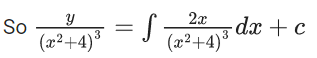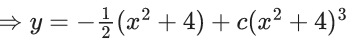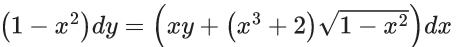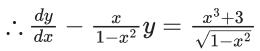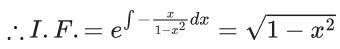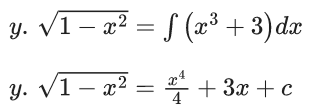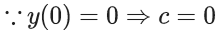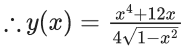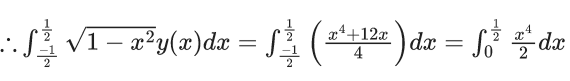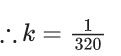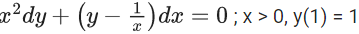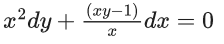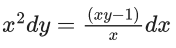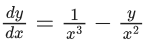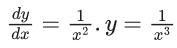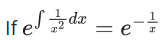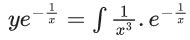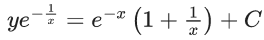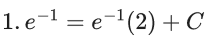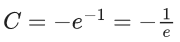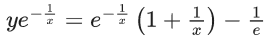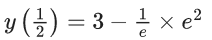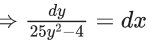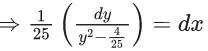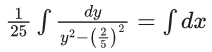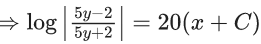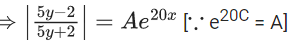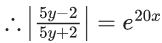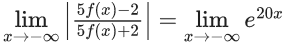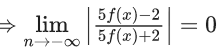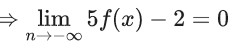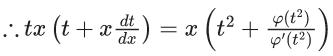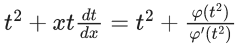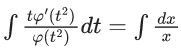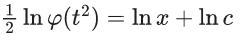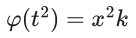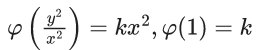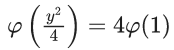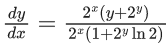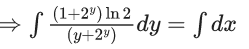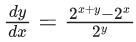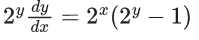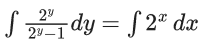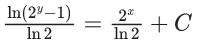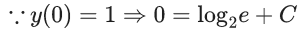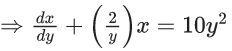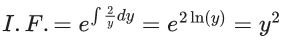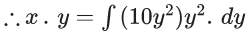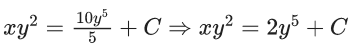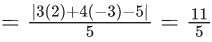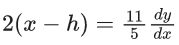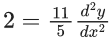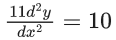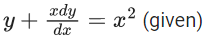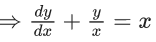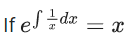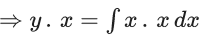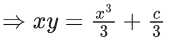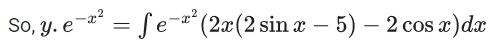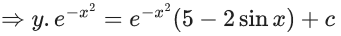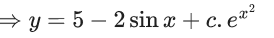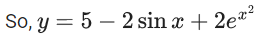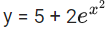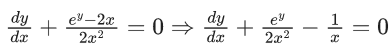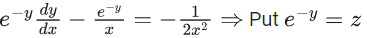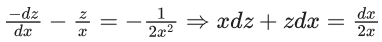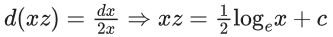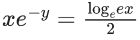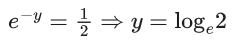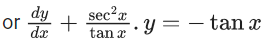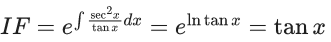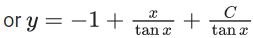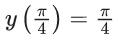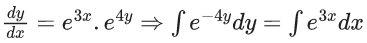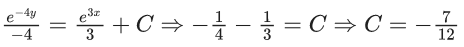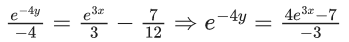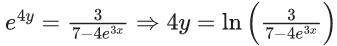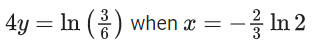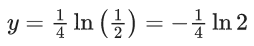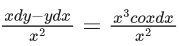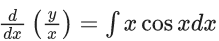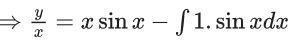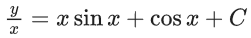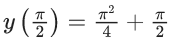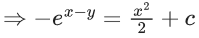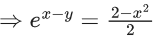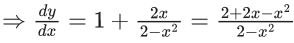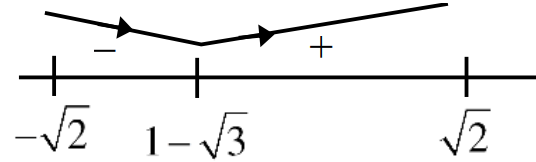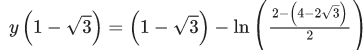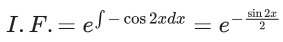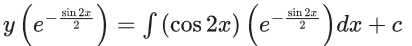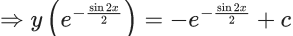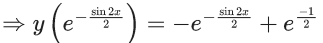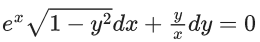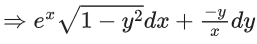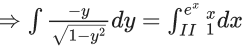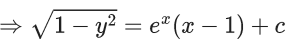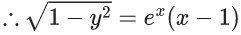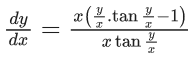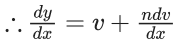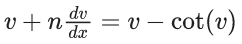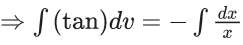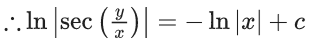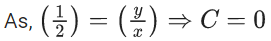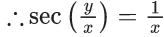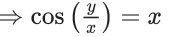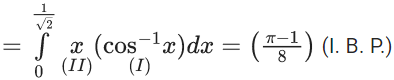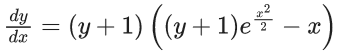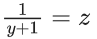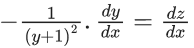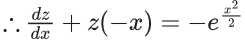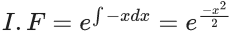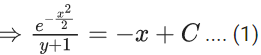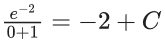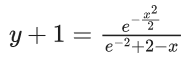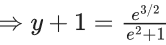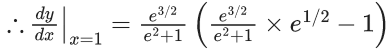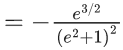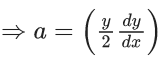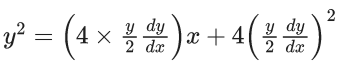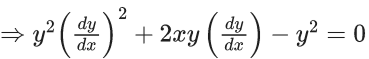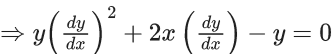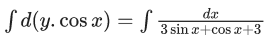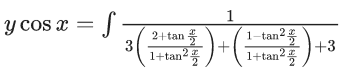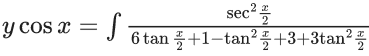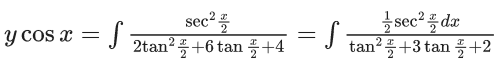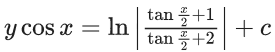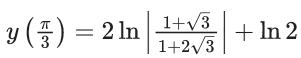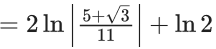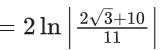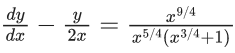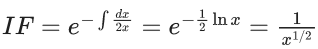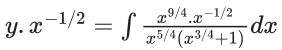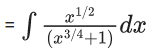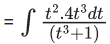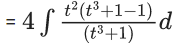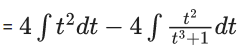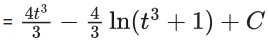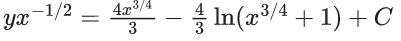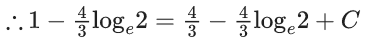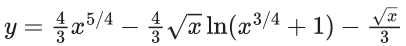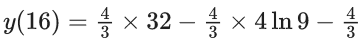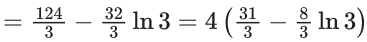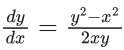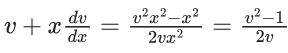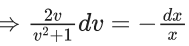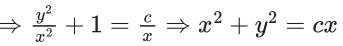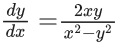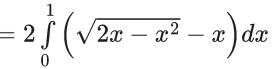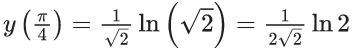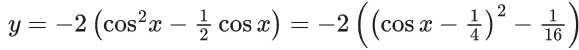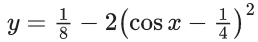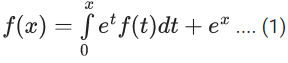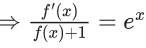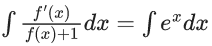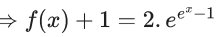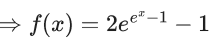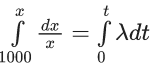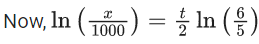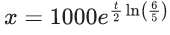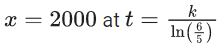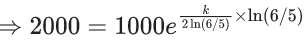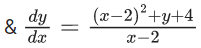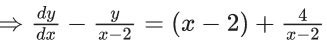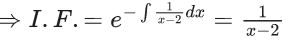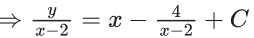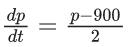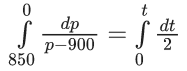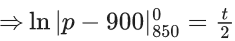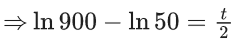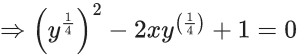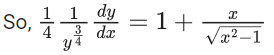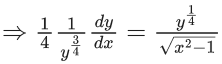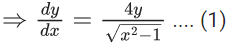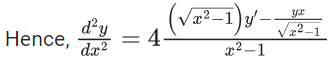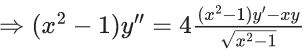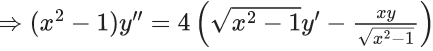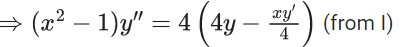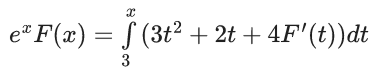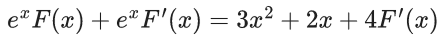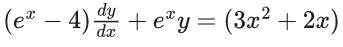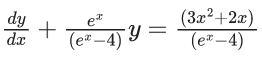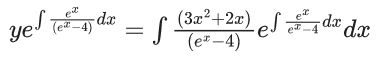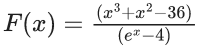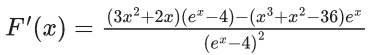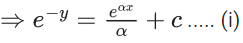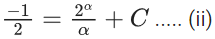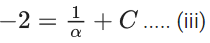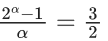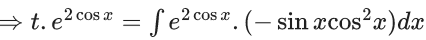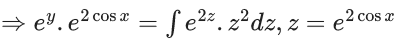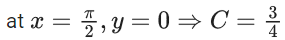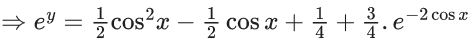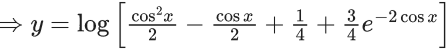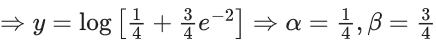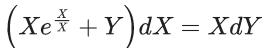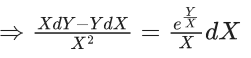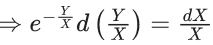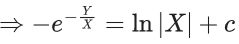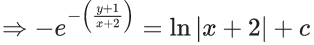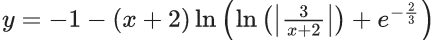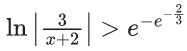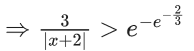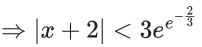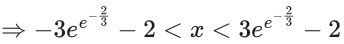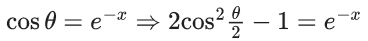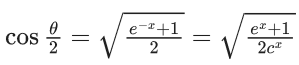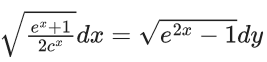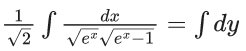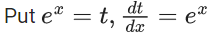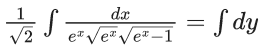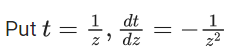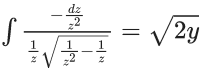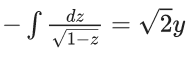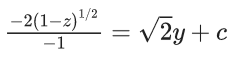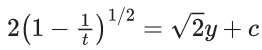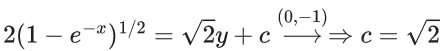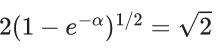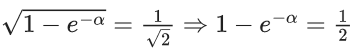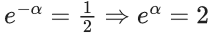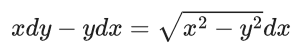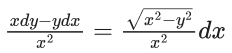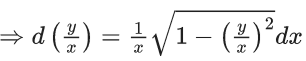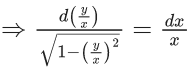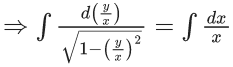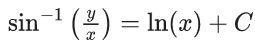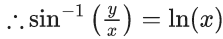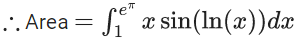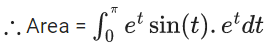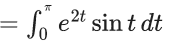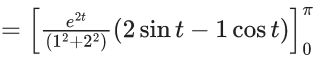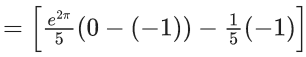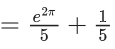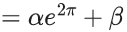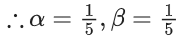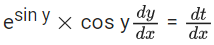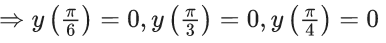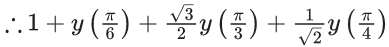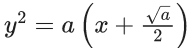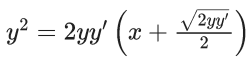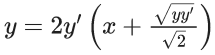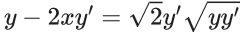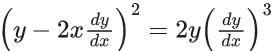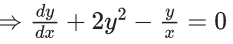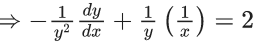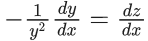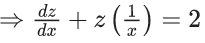JEE Main Previous year questions (2021-23): Differential Equations PDF Download

Q.1. Let y = y(x) be the solution of the differential equation x³ dy + (xy − 1)dx = 0, x > 0, y (1/2) = 3 - e.
Then y(1) is equal to      (JEE Main 2023)
(a) 1
(b) e
(c) 3
(d) 2 – e

Ans. a
x³ dy + (xy – 1) dx = 0

Q.2. Let y = y(x) be the solution of the differential equation (x² − 3y²)dx + 3xydy = 0, y(1) = 1.

Then 6y²(e) is equal to       (JEE Main 2023)
(a) 2e2
(b) 3e2
(c) e2
(d)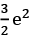

Ans. a

Q.3. Let f be a differentiable function defined on 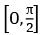 such that f(x) > 0 and
 is equal to      (JEE Main 2023)

Ans. 27

Q.4. For  let the function y(x) be the solution of the differential equation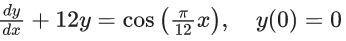

Then, which of the following statements is/are TRUE ?      (JEE Advanced 2022)
(a) y(x) is an increasing function
(b) y(x) is a decreasing function
(c) There exists a real number β such that the line y=β intersects the curve y=y(x) at infinitely many points
(d) y(x) is a periodic function

Ans. c

Q.5. If y(x) is the solution of the differential equation for xdy − (y² − 4y)dx = 0 for x > 0, y(1) = 2, and the slope of the curve y = y(x) is never zero, then the value of 10y(√2) is     (JEE Advanced 2022)

Ans. 8
xdy = (y² - 4y)dx = 0
⇒ xdy = (y² - 4y)dx




Integrating both side, we get




Given, y(1) = 2

⇒ λ = -1



⇒ y − 4 = −4y
⇒ 5y = 4
⇒ y = 45
∴ 10y(√2) = 10 x (4/5) = 8

Q.6. Let y = y(x) be the solution curve of the differential equation 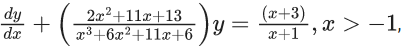 which passes through the point (0, 1). Then y(1) is equal to :     (JEE Main 2022)
(a) 1/2
(b) 3/2
(c) 5/2
(d) 7/2

Ans. b

Integrating factor I.F.
 Let
A = 2, B = 1, C = -1
 I.F. = e(2In|x+1) + In|x+2| - In|x+3|)

Solution of differential equation


Curve passes through (0, 1)

 So,

Q.7. If the solution curve of the differential equation  passes through the points (2, 1) and (k+1, 2), k > 0, then     (JEE Main 2022)
(a)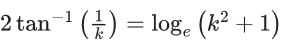
(b)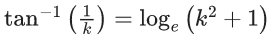
(c)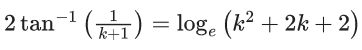
(d)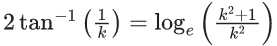

Ans. a

Let x − 1 = X, y − 1 = Y







Curve passes through (2,1)
0 − 0 = 0 + c ⇒ c = 0
If (k + 1, 2) also satisfies the curve

Q.8. Let the solution curve y = y(x) of the differential equation 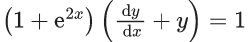  pass through the point  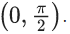Then, 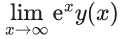  is equal to :     (JEE Main 2022)
(a) π/4
(b) 3π/4
(c) π/2
(d) 3π/2

Ans. b



∴ Solution

⇒ e^xy(x) = tan⁻¹(e^x) + C
∵ It passes through

= 3π/4

Q.9. The differential equation of the family of circles passing through the points (0, 2) and (0, −2) is :    (JEE Main 2022)
(a)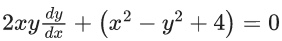
(b)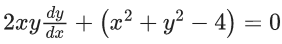
(c)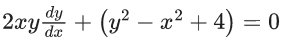
(d)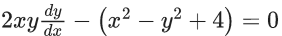

Ans. a
Family of circles passing through the points (0, 2) and (0, −2)
x² + (y − 2)(y + 2) + λx = 0, λ ∈ R
x² + y² + λx − 4 = 0 ...... (1)
Differentiate w.r.t x

Using (1) and (2), eliminate λ

Q.10. Let y = y(x) be the solution curve of the differential equation 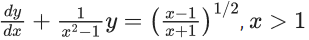 passing through the point  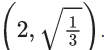Then √7y(8) is equal to :       (JEE Main 2022)
(a) 11 + 6log_e⁡3
(b) 19
(c) 12 − 2log_e⁡3
(d) 19 − 6log_e⁡3

Ans. d

Integrating factor I.F.

Solution of differential equation

Curve passes through



√7 .y(8) = 19 - 6 In 3

Q.11. The minimum value of the twice differentiable function 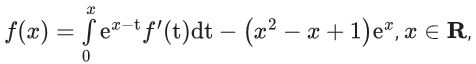 is :      (JEE Main 2022)
(a)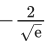
(b)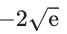
(c)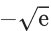
(d)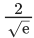

Ans. a



Differentiate on both side
e^−xf′(x) + (−f(x)e^−x) = e^−xf′(x) − 2x + 1
f(x) = e^x(2x − 1)
f′(x) = e^x(2) + e^x(2x − 1)
= e^x(2x + 1)
x = −(1/2)
f″(x) = e^x(2) + (2x+1)e^x
= e^x(2x + 3)
For x = -(1/2) f"(x) > 0
⇒ Maxima

Q.12. If y = y(x), x ∈ (0, π/2) be the solution curve of the differential equation (sin²⁡2x)(dy/dx) + (8sin²⁡2x + 2sin⁡4x)y = 2e^−4x(2sin⁡2x + cos⁡2x), with y(π/4) = e^−π, then y(π/6) is equal to :      (JEE Main 2022)
(a)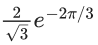
(b)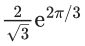
(c)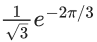
(d)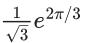

Ans. a



Integrating factor
(I.F.) = e^{∫(8 + 4cot⁡2x)dx}
= e^{8x+2ln⁡sin⁡2x}
Solution of differential equation
y.e^{8x + 2ln⁡sin⁡2x}

Q.13. Let the solution curve of the differential equation 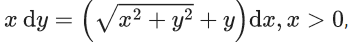 intersect the line x = 1 at y = 0 and the line x = 2 at y = α. Then the value of α is :      (JEE Main 2022)
(a) 1/2
(b) 3/2
(c) -(3/2)
(d) 5/2

Ans. b







at x = 1, y = 0
⇒ C = 0

At x = 2,


OR y = 3/2

Q.14. Let y = y₁(x) and y = y₂(x) be two distinct solutions of the differential equation dy/dx = x + y, with y₁(0) = 0 and y₂(0) = 1 respectively. Then, the number of points of intersection of y = y₁(x) and y = y₂(x) is     (JEE Main 2022)
(a) 0
(b) 1
(c) 2
(d) 3

Ans. a
dy/dx = x + y
Let x + y = t


ln⁡|t + 1| = x + C′
|t + 1| = Ce^x
|x + y + 1| = Ce^x
For y₁(x), y₁(0) = 0 ⇒ C = 1
For y₂(x), y₂(0) = 1 ⇒ C = 2
y₁(x) is given by |x + y + 1| = ex
y₂(x) is given by |x + y + 1| = 2ex
At point of intersection
e^x = 2e^x
No solution
So, there is no point of intersection of y₁(x) and y₂(x).

Q.15. Let the solution curve y=f(x) of the differential equation 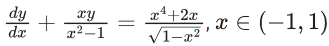 pass through the origin. Then  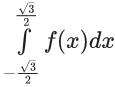is equal to     (JEE Main 2022)
(a)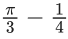
(b)
(c)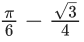
(d)

Ans. b

which is first order linear differential equation.
Integrating factor


∵ x ∈ (−1, 1)
Solution of differential equation

Curve is passing through origin, c = 0


put x = sin⁡θ
dx = cos⁡θdθ

Q.16. If (dy/dx) + 2y tanx = sinx, 0 < x < (π/2) and y(π/3) = 0, then the maximum value of y(x) is :     (JEE Main 2022)
(a) 1/8
(b) 3/4
(c) 1/4
(d) 3/8

Ans. a
(dy/dx) + 2y tanx = sinx
which is a first order linear differential equation.
Integrating factor (I. F.) = e^∫2tanxdx
= e^{2ln⁡|sec⁡x|} = sec²x
Solution of differential equation can be written as
y . sec²x = ∫sin⁡x . sec²x dx = ∫secx . tan⁡ x dx
y sec²x = sec⁡x + C



y_max = 1/8

Q.17. The general solution of the differential equation (x − y²)dx + y(5x + y²)dy = 0 is :     (JEE Main 2022)
(a) (y²+x)⁴ = C|(y²+2x)³|
(b) (y²+2x)⁴ = C|(y²+x)³|
(c) |(y²+x)³| = C(2y²+x)⁴
(d) |(y²+2x)³| = C(2y²+x)⁴

Ans. a
(x−y²)dx + y(5x+y²)dy = 0


Now substitute, t = vx

|(y² + x)⁴| = C|(y² + 2x)³|

Q.18. If x = x(y) is the solution of the differential equation ((y)(dx/dy)) = 2x + y³(y + 1)e^y, x(1) = 0; then x(e) is equal to :     (JEE Main 2022)
(a) e³(e^e - 1)
(b) e^e(e³- 1)
(c) e²(e^e + 1)
(d) e^e(e² - 1)

Ans. a


Solution is given by



⇒ x = y²(ye^y + c) at, y=1,x=0
⇒ 0 = 1(1⋅e¹ + c) ⇒ c = −e at y = e,
x = e²(e.e^e − e)

Q.19. If the solution curve y = y(x) of the differential equation y²dx + (x² − xy + y²)dy = 0, which passes through the point (1, 1) and intersects the line y = √3x at the point (α, √3α), then value of log_e(√3α) is equal to :      (JEE Main 2022)
(a) π/3
(b) π/2
(c) π/12
(d) π/6

Ans. c

Put y = vx we get




As it passes through (1, 1)
c = π/4

Put y = √3x we get

Q.20. Let y = y(x) be the solution of the differential equation (x + 1)y′ − y = e^3x(x + 1)², with y(0) = (1/3). Then, the point x = −(4/3) for the curve y = y(x) is :     (JEE Main 2022)
(a) not a critical point
(b) a point of local minima
(c) a point of local maxima
(d) a point of inflection

Ans. b






∵ y(0) = (1/3)

∴ c = 0




⇒ x = (−4)/3 is point of local minima.

Q.21. If y = y(x) is the solution of the differential equation 2x²(dy/dx) - 2xy + 3y² = 0 such that y(e) = e/3, then y(1) is equal to     (JEE Main 2022)
(a) 1/3
(b) 2/3
(c) 3/2
(d) 3

Ans. b

y = 2/3

Q.22. Let g : (0, ∞) → R be a differentiable function such that 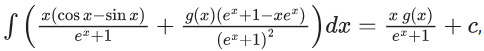 for all x > 0, where c is an arbitrary constant. Then :      (JEE Main 2022)
(a) g is decreasing in (0,π4)
(b) g' is increasing in (0,π4)
(c) g + g' is increasing in (0,π2)
(d) g − g' is increasing in (0,π2)

Ans. d

On differentiating both sides w.r.t. x, we get






g(x) is increasing in (0, π/4)
g"(x) = −sin⁡x − cos⁡x < 0
⇒ g′(x) is decreasing function
let h(x) = g(x) + g′(x) = 2cos⁡x + C
⇒ h′(x) = g′(x) + g′′(x) = −2sin⁡x < 0
⇒ h is decreasing
let ϕ(x) = g(x) − g′(x) = 2sin⁡x + C
⇒ ϕ′(x) = g′(x) − g′′(x) = 2cos⁡x > 0
⇒ ϕ is increasing
Hence option D is correct.

Q.23. If the solution of the differential equation (dy/dx) + e^x(x² − 2)y = (x²−2x)(x²−2)e^2x satisfies y(0) = 0, then the value of y(2) is ______.      (JEE Main 2022)
(a) -1
(b) 1
(c) 0
(d) e

Ans. c



∴ Solution of the differential equation is


Let (x² − 2x)ex = t
∴ (x² − 2)e^xdx = dt

∴ y(0) = 0
∴ c = 1

∴ y(2) = −1 + 1 = 0

Q.24. If y = y(x) is the solution of the differential equation x(dy/dx) +2y = xe^x, y(1) = 0 then the local maximum value of the function z(x) = x²y(x) − e^x, x ∈ R is :     (JEE Main 2022)
(a) 1 - e
(b) 0
(c) 1/2
(d) (4/e) - e

Ans. d



For local maximum z'(x) = 0
∴ 2(x−1)e^x + (x−1)²e^x = 0
∴ x = −1
And local maximum value = z(−1)
= (4/e) − e

Q.25. If 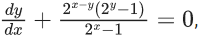 x, y > 0, y(1) = 1, then y(2) is equal to:     (JEE Main 2022)
(a) 2 + log₂3
(b) 2 + log₃2
(c) 2 - log₃2
(d) 2 - log₂3

Ans. d




= |(2^y−1)(2^x−1)| = c
∵ y(1) = 1
∴ c = 1
= |(2^y−1)(2^x−1)| = 1
For x = 2
|(2^y−1)3| = 1
2y−1 = (1/3) ⇒ 2y = (4/3)
Taking log to base 2.
∴ y = 2 − log₂3

Q.26. If the solution curve of the differential equation ((tan⁻¹y)−x)dy = (1+y²)dx passes through the point (1, 0), then the abscissa of the point on the curve whose ordinate is tan(1), is      (JEE Main 2022)
(a) 2e
(b) 2/e
(c) 2
(d) 1/e

Ans. b



∴ Solution





∵ It passes through (1, 0) ⇒ c = 2
Now put y = tan1, then
ex = e−e + 2
⇒ x = 2e

Q.27. Let y = y(x) be the solution of the differential equation x(1−x²)(dy/dx) + (3x²y−y−4x³) = 0, x > 1, with y(2) = −2. Then y(3) is equal to       (JEE Main 2022)
(a) -18
(b) -12
(c) -6
(d) -3

Ans. a


Solution of D.E. can be given by



at x = 2, y = −2

Q.28. Let the solution curve y = y(x) of the differential equation 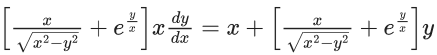 pass through the points (1, 0) and (2α, α), α > 0. Then α is equal to     (JEE Main 2022)
(a)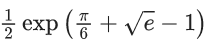
(b)
(c)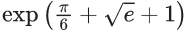
(d)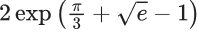

Ans. a

Putting y = tx




at x = 1, y = 0
So, 0 + e⁰ = 0 + C ⇒ C = 1
at (2α, α)
sin⁻¹(y/x)+e^y/x = ln⁡x+1
⇒ π/6 + e^(1/2)−1 = ln⁡(2α)

Q.29. Let x = x(y) be the solution of the differential equation 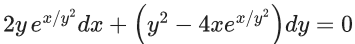 such that x(1) = 0. Then, x(e) is equal to :       (JEE Main 2022)
(a) elog_e(2)
(b) -elog_e(2)
(c) e²log_e(2)
(d) -e²log_e(2)

Ans. d
Given differential equation





Now, using x(1) = 0, c = 2
So, for x(e), Put y = e in (i)

Q.30. If y = y(x) is the solution of the differential equation 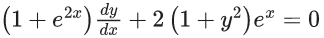 and y (0) = 0, then  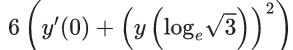is equal to       (JEE Main 2022)
(a) 2
(b) -2
(c) -4
(d) -1

Ans. c
Given,


Now,
Let ex = t
⇒ e^xdx = dt

⇒ tan−1(y)= −2tan⁻¹(t) + C
⇒ tan−1(y)= −2tan⁻¹(e^x) + C [Putting value of t]
Given, y(0) = 0 means when x = 0 the y = 0
∴ tan⁻¹(0) = −2tan⁻¹(e^o) + C
⇒ 0 = −2 × (π/4) + C
⇒ C = (π/2)
∴ tan⁻¹(y) = 2tan⁻¹(e^x) + π/2
⇒ y = tan⁡(−2tan⁻¹(e^x) + π/2)
Differentiating both sides, we get


= sec²(0)x − 1
= 1 × 1
= −1
And

Q.31. Let the solution curve of the differential equation 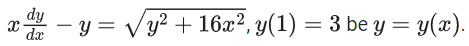 Then y(2) is equal to:     (JEE Main 2022)
(a) 15
(b) 11
(c) 13
(d) 17

Ans. a
Given,

This is a homogenous different equation.
Let (y/x) = v
⇒ y  = vx




Integrating both sides, we get

Now putting, v = (y/x), we get

Given, y(1) = 3
∴ When x = 1 then y = 3.
Putting in equation (1) we get,

⇒ c = 8
∴ Solution of equation,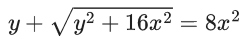
 
Now, y(2) means when x = 2 then y = ?

⇒ y = 15

Q.32. Suppose y = y(x) be the solution curve to the differential equation (dy/dx) − y = 2 − e^−x such that 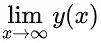 is finite. If a and b are respectively the x - and y-intercepts of the tangent to the curve at x = 0, then the value of a − 4b is equal to ____.     (JEE Main 2022)

Ans. 3
IF = e^−x

⇒ y = −2 + e^−x + Ce^x
 is finite 

so C = 0y = −2 + e^−x

Equation of tangenty + 1 = −1(x − 0)
or y + x = −1
So a = −1, b = −1
⇒ a − 4b = 3

Q.33. Let f be a twice differentiable function on 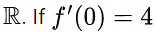 and 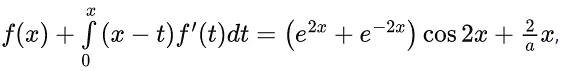 then (2a + 1)⁵a² is equal to _____.     (JEE Main 2022)

Ans. 8

Q.34. Let y = y(x) be the solution of the differential equation 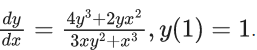 If for some  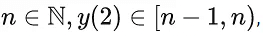 then n is equal to ____.     (JEE Main 2022)

Ans. 3

Put y = vx

⇒ C = ln⁡2

∴ for y(2)

⇒ [y(2)] = 2⇒ n = 3

Q.35. Let 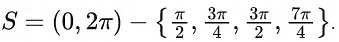 Let y = y(x), x ∈ S, be the solution curve of the differential equation  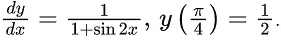If the sum of abscissas of all the points of intersection of the curve y = y(x) with the curve  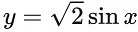is kπ/12, then k is equal to ______.     (JEE Main 2022)

Ans. 42

sin⁡x = 0 gives x = π only.

Sum of all solutions

Hence, k = 42.

Q.36. Let the solution curve y = y(x) of the differential equation (4+x²)dy − 2x(x² + 3y + 4)dx  = 0 pass through the origin. Then y(2) is equal to _____.      (JEE Main 2022)

Ans. 12
(4 + x²)dy - 2x(x² + 3y + 4)dx = 0





When x = 0, y = 0 gives c = 1/32,
So, for x = 2, y = 12

Q.37. Let y = y(x) be the solution of the differential equation 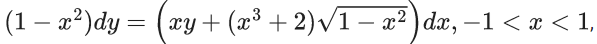 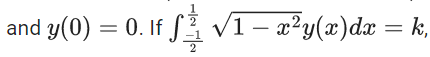 then k⁻¹ is equal to _____.    (JEE Main 2022)

Ans. 320



Solution is





∴ = k^-1 = 320.

Q.38. Let y = y(x), x > 1, be the solution of the differential equation 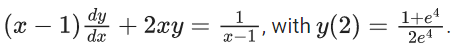 If 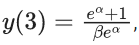 then the value of α + β is equal to _____.      (JEE Main 2022)

Ans. 14

Q.39. Let y = y(x) be the solution of the differential equation 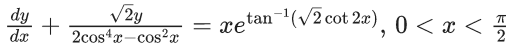 with 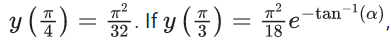 then the value of 3α² is equal to ____.      (JEE Main 2022)

Ans. 2

Q.40. If y = y(x) is the solution curve of the differential equation 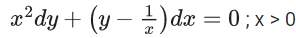 and y(1) = 1, then y(1/2) is equal to :     (JEE Main 2021)
(a)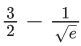
(b)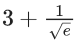
(c) 3 + e
(d) 3 - e

Ans. d

y(1/2) = 3 - e

Q.41. Let f : R → R be a differentiable function with f(0) = 0. If y = f(x) satisfies the differential equation (dy/dx) = (2 + 5y)(5y − 2), then the value of 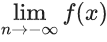 is ____.     (JEE Advanced 2021)

Ans. 0.4

We have,
dy/dx = (2 + 5y)(5y - 2)


On integrating both sides, we get




when x = 0 ⇒ y = 0, then A = 1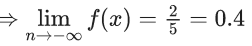




 

Q.42. If 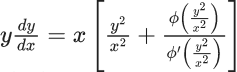 x > 0, ϕ > 0, and y(1) = −1, then  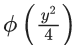is equal to :      (JEE Main 2021)
(a) 4 ϕ (2)
(b) 4 ϕ (1)
(c) 2 ϕ (1)
(d) ϕ (1)

Ans. b
Let, y = tx




Let φ(t²) = p
∴ φ′(t²)2tdt = dp

Q.43. If 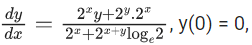 then for y = 1, the value of x lies in the interval :     (JEE Main 2021)
(a) (1, 2)
(b) ((1/2), 1]
(c) (2, 3)
(d) (0, (1/2)]

Ans. a


⇒ ln⁡|y + 2^y|= x + c
x = 0; y = 0 ⇒ c = 0
⇒ x = ln⁡|y + 2^y|
⇒ at y = 1, x = ln3
∵ 3 ∈ (e, e²) ⇒ x ∈ (1,2)

Q.44. If 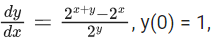 then y(1) is equal to :     (JEE Main 2021)
(a) log₂(2 + e)
(b) log₂(1 + e)
(c) log₂(2e)
(d) log₂(1 + e²)

Ans. b






C = −log₂e
⇒ log₂(2^y − 1) = (2^x − 1)log₂e
put x = 1, log₂(2^y − 1) = log₂e
2^y = e + 1
y = log₂(e + 1) Ans.

Q.45. If the solution curve of the differential equation (2x − 10y³)dy + ydx = 0, passes through the points (0, 1) and (2, β), then β is a root of the equation :      (JEE Main 2021)
(a) y⁵ − 2y − 2 = 0
(b) 2y⁵ − 2y − 1 = 0
(c) 2y⁵ − y² − 2 = 0
(d) y⁵ − y² − 1 = 0

Ans. d
(2x − 10y³)dy + ydx = 0


Solution of D.E. is


It passes through (0, 1) → 0 = 2 + C ⇒ C = −2
∴ Curve is xy² = 2y⁵ − 2
Now, it passes through (2, β)
2β² = 2β⁵ − 2 ⇒ β⁵ − β² − 1 = 0
∴ β is root of an equation y⁵ − y² − 1 = 0

Q.46. A differential equation representing the family of parabolas with axis parallel to y-axis and whose length of latus rectum is the distance of the point (2, −3) from the line 3x + 4y = 5, is given by :      (JEE Main 2021)
(a)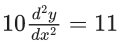
(b)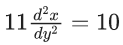
(c)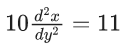
(d)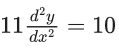

Ans. d
Length of latus rectum

(x−h)² = (11/5)(y−k)
differentiate w.r.t. 'x' :-

again differentiate

Q.47. Let us consider a curve, y = f(x) passing through the point (−2, 2) and the slope of the tangent to the curve at any point (x, f(x)) is given by f(x) + xf'(x) = x². Then :      (JEE Main 2021)
(a) x² + 2xf(x) − 12 = 0
(b) x³ + xf(x) + 12 = 0
(c) x³ − 3xf(x) − 4 = 0
(d) x² + 2xf(x) + 4 = 0

Ans. c



Solution of DE


Passes through (−2, 2), so
−12 = − 8 + c ⇒ c = − 4
∴ 3xy = x³ − 4
i.e. 3x . f(x) = x³ − 4

Q.48. Let y = y(x) be the solution of the differential equation (dy/dx) = 2(y + 2sin⁡x−5)x − 2cos⁡x such that y(0) = 7. Then y(π) is equal to :      (JEE Main 2021)
(a)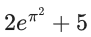
(b)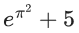
(c)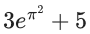
(d)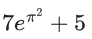

Ans. a
(dy/dx) − 2xy = 2(2sin⁡x − 5)x − 2cos⁡x




Given at x = 0, y = 7
⇒ 7 = 5 + c ⇒ c = 2

Now, at x = π,

Q.49. Let y(x) be the solution of the differential equation 2x² dy + (ey − 2x)dx = 0, x > 0. If y(e) = 1, then y(1) is equal to :    (JEE Main 2021)
(a) 0
(b) 2
(c) log_e 2
(d) log_e (2e)

Ans. c
2x²dy + (e^y − 2x)dx = 0




xe^−y = (1/2)log_ex + c, passes through (e, 1)
⇒ C = 1/2

Q.50. Let y = y(x) be a solution curve of the differential equation (y + 1)tan²xdx + tan ⁡x dy + y dx = 0, x ∈ (0, (π/2)). If  then the value of y(π/4) is :     (JEE Main 2021)
(a) -(π/4)
(b) (π/4) - 1
(c) (π/4) + 1
(d) (π/4)

Ans. d
(y+1)tan² x dx + tan ⁡x dy + y dx = 0


∴ y tan⁡ x = −∫tan²x dx

or y tan ⁡x = −tan⁡x + x + C


or C = 1
y(x) = cot ⁡x + x cot⁡ x − 1

Q.51. Let y = y(x) be solution of the differential equation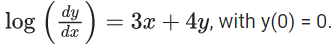
 If 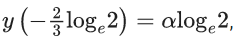  then the value of α is equal to :      (JEE Main 2021)
(a) -(1/4)
(b) (1/4)
(c) 2
(d) -(1/2)

Ans. a

Q.52. Let y = y(x) be the solution of the differential equation xdy = (y + x³ cosx)dx with y(π) = 0, then y(π/2) is equal to :       (JEE Main 2021)
(a)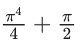
(b)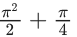
(c)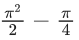
(d)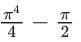

Ans. a
xdy = (y + x³cos⁡x)dx
xdy = ydx + x³cos ⁡x dx




⇒ 0 = −1 + C ⇒ C = 1, x = π, y = 0
so, y/x = xsin⁡x + cos⁡x + 1
y = x²sin⁡x + xcos⁡x + x
x = π/2

Q.53. Let y = y(x) be the solution of the differential equation (x − x³)dy = (y + yx² − 3x⁴)dx, x > 2. If y(3) = 3, then y(4) is equal to :     (JEE Main 2021)
(a) 4
(b) 12
(c) 8
(d) 16

Ans. b
(x−x³)dy = (y+yx²−3x⁴)dx
⇒ xdy−ydx = (yx²−3x⁴)dx + x³dy
⇒ (xdy−ydx)/x² = (ydx+xdy) − 3x²dx
⇒ d(y/x) = d(xy)−d(x³)
Integrate
⇒ y/x = xy − x³ + c
given f(3) = 3
⇒ (3/3) =3×3−3³+c
⇒ c = 19
∴ y/x = xy − x³ + 19
at x = 4, y/4 = 4y − 64 + 19
15y = 4 × 45
⇒ y = 12

Q.54. Let y = y(x) be the solution of the differential equation (dy/dx) = 1 + xe^y−x, −√2 < x < 2, y(0) = 0 then, the minimum value of y(x), x ∈ (−√2, √2) is equal to :     (JEE Main 2021)
(a) (2 − √3) − log_e2
(b) (2 + √3) + log_e2
(c) (1 + √3) − log_e (√3−1)
(d) (1 − √3) − log_e (√3−1)

Ans. d



At x = 0, y = 0 ⇒ c = −1

So minimum value occurs at x = 1 − √3

=(1−√3) − ln⁡(√3−1)

Q.55. Let y = y(x) be the solution of the differential equation cos⁡ ec²xdy + 2dx = (1 + ycos⁡2x)cos⁡ ec² xdx, with y(π/4) = 0. Then, the value of (y(0) + 1)² is equal to :      (JEE Main 2021)
(a) e^1/2
(b) e^(-1/2)
(c) e^-1
(d) e

Ans. c
(dy/dx) + 2sin²x = 1 + ycos⁡2x
⇒ (dy/dx) + (−cos⁡2x)y = cos⁡2x

Solution of D.E.


Given
y(π/4) = 0
⇒ 0 = −e^(−1/2) + c ⇒ c = e^(−1/2)

at x = 0
y= −1 + e^(−1/2)
⇒ y(0) = −1 + e^(−1/2) ⇒ (y(0) + 1)² = e⁻¹

Q.56. Let y = y(x) be the solution of the differential equation 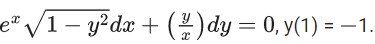 Then the value of (y(3))² is equal to :     (JEE Main 2021)
(a) 1 - 4e³
(b) 1 − 4e⁶
(c) 1 + 4e³
(d) 1 + 4e⁶

Ans. b




Given : At x = 1, y = −1
⇒ 0 = 0 + c ⇒ c = 0

At x = 3
1 − y² = (e³2)² ⇒ y² = 1 − 4e⁶

Q.57. Let y = y(x) be the solution of the differential equation x tan⁡(y/x)dy = (ytan⁡(y/x) − x)dx, −1 ≤ x ≤ 1, y(1/2) = (π/6). Then the area of the region bounded by the curves x = 0, x = (1/√2) and y = y(x) in the upper half plane is :      (JEE Main 2021)
(a) (1/8)(π - 1)
(b)  (1/12)(π - 3)
(c)  (1/4)(π - 2)
(d)  (1/6)(π - 1)

Ans. a
We have,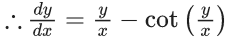 

 
Put (y/x) = v
⇒ y = vn

Now, we get






∴ y = xcos⁻¹(x)
So, required bounded area

∴ Option (1) is correct.

Q.58. Let y = y(x) be the solution of the differential equation 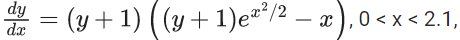 with y(2) = 0. Then the value of (dy/dx) at x = 1 is equal to :      (JEE Main 2021)
(a)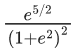
(b)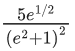
(c)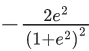
(d)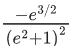

Ans. d


Put,





Given y = 0 at x = 2 Put in (1)

C = e⁻² + 2 .... (2)
From (1) and (2)

Again, at x = 1

Q.59. The differential equation satisfied by the system of parabolas y² = 4a(x + a) is :     (JEE Main 2021)
(a)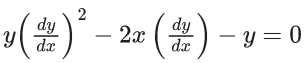
(b)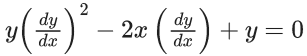
(c)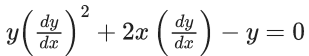
(d)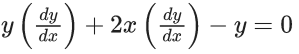

Ans. c
y² = 4ax + 4a²
differentiate with respect to x
⇒ 2y(dy/dx) = 4a

So, required differential equation is

Q.60. Let y = y(x) be the solution of the differential equation cos⁡ x(3sin⁡x + cos⁡x + 3)dy = (1 + y sin ⁡x(3sin⁡x + cos⁡x + 3))dx, 0 ≤ x ≤ π/2, y(0) = 0. Then, y(π/3) is equal to :      (JEE Main 2021)
(a)
(b)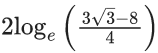
(c)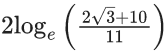
(d)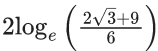

Ans. c
cos⁡x(3sin⁡x + cos⁡x + 3)dy = (1 + ysin⁡x(3sin⁡x + cos⁡x + 3))dx ..... (1)
(3sin⁡x + cos⁡x + 3)(cos⁡ x dy − y sin⁡ x dx) = dx





Put x = 0 & y = 0
C = −ln⁡(1/2) = ln⁡(2)

Q.61. If the curve y = y(x) is the solution of the differential equation 2(x² + x^5/4)dy − y(x + x^1/4)dx = 2^9/4dx, x > 0 which passes through the point (1, 1−(4/3) log_e2), then the value of y(16) is equal to :     (JEE Main 2021)
(a)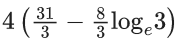
(b)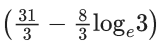
(c)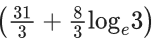
(d)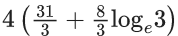  

Ans. a




Let, x = t⁴ ⇒ dx = 4t³dt





It passes through the point (1, 1 - (4/3)log_e2)

⇒ C = -(1/3)

Q.62. Which of the following is true for y(x) that satisfies the differential equation
(dy/dx) = xy − 1 + x − y; y(0) = 0 :     (JEE Main 2021)
(a) y(1) = 1
(b) y(1) = e^-(1/2) - 1
(c) y(1) = e^-(1/2) - e^-(1/2)
(d) y(1) = e^(1/2) - 1

Ans. b
dy/dx = (x−1)y+(x−1)
dy/dx = (x−1)(y+1)
dy/(y+1) = (x−1)dx
Integrating both sides, we get
ln⁡(y + 1) = x²/2 − x + c
x = 0, y = 0
⇒ c = 0
∴ ln⁡(y+1) = (x²/2) − x
putting x = 1, ln⁡(y+1) = (1/2) −1 = −(1/2)
y+1 = e^−(1/2)
y = e^−(1/2)−1
∴ y(1) = e^−(1/2)−1

Q.63. Let C₁ be the curve obtained by the solution of differential equation 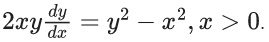 Let the curve C₂ be the solution of 

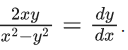 If both the curves pass through (1, 1), then the area enclosed by the curves C₁ and C₂ is equal to :     (JEE Main 2021)
(a) (π/4) + 1
(b) π + 1
(c) π - 1
(d) (π/2) - 1

Ans. d

Put y = vx



ln ⁡(v²+1) = −ln⁡ x + ln ⁡c ⇒ v² + 1 = (c/x)

It pass through (1, 1)
∴ x² + y² - 2x = 0
Similarly for second differential equation
Equation of curve is x² + y² − 2y = 0
Now required area is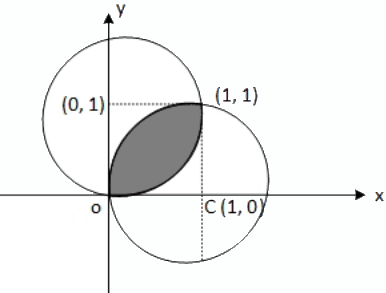
 

 

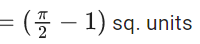
Q.64. If y = y(x) is the solution of the differential equation (dy/dx) + (tan x) y = sin x, 0 ≤ x ≤ (π/3), with y(0) = 0, then y(π/4) equal to :      (JEE Main 2021)
(a) (1/2)(log_e 2)
(b) (1/(2√2)) (log_e 2)
(c) log_e 2
(d) (1/4)log_e2

Ans. b
Integrating Factor = e^∫tan⁡xdx = e^{ln⁡(sec⁡x)} = sec⁡ x
y sec⁡ x = ∫(sin⁡ x) sec⁡ x dx = ln⁡(sec⁡ x) + C
y(0) = 0 ⇒ C = 0
∴ y = cos ⁡x ln ⁡|sec ⁡x|

Q.65. If y = y(x) is the solution of the differential equation, (dy/dx) + 2ytan⁡x = sin⁡x, y(π/3) = 0, then the maximum value of the function y(x) over R is equal to:      (JEE Main 2021)
(a) 1/8
(b) 8
(c) -(15/4)
(d) 1/2

Ans. a
(dy/dx) +2tan⁡x.y = sin⁡x
I.F. = e^{2ln⁡(sec⁡x)} = sec²x
y.sec²x = ∫ sin ⁡x sec²xdx = ∫ tan⁡ x sec ⁡x dx + c
ysec²x = sec ⁡x + c
y = cos⁡x + ccos²x
x = π/3, y = 0
⇒ (1/2) + (c/4) ⇒ c = −2
∴ y = cos⁡x − 2cos²x


∴ y_max = 1/8

Q.66. Let 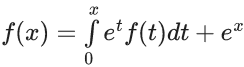 be a differentiable function for all x ∈ R. Then f(x)  equals :     (JEE Main 2021)
(a)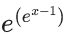
(b)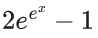
(c)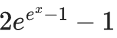
(d)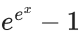

Ans. c

Differentiating both sides w.r.t. x
f′(x) = e^x.f(x) + e^x (Using Newton L:eibnitz Theorem)

Integrating w.r.t. x

⇒ ln⁡(f(x) + 1) = e^x + c
Put x = 0
ln 2 = 1 + c (∵ f(0) = 1, from equation (1))
∴ ln⁡(f(x) + 1) = e^x + ln⁡ 2 − 1

Q.67. The rate of growth of bacteria in a culture is proportional to the number of bacteria present and the bacteria count is 1000 at initial time t = 0. The number of bacteria is increased by 20% in 2 hours. If the population of bacteria is 2000 after 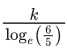 hours, then  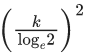is equal to :     (JEE Main 2021)
(a) 16
(b) 8
(c) 2
(d) 4

Ans. d
(dx/dt) ∝ x
(dx/dt) = λx

ln ⁡x − ln⁡ 1000 = λt
ln⁡(x/1000) = λt
Put t = 2, x = 1200





⇒ 2 = e^k/2
⇒ ln ⁡2 = (k/2)
⇒ (k/ln⁡ 2) = 2
⇒ (k/ln ⁡2)² = 4

Q.68. If a curve passes through the origin and the slope of the tangent to it at any point (x, y) is 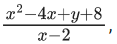 then this curve also passes through the point :      (JEE Main 2021)
(a) (4, 4)
(b) (5, 5)
(c) (5, 4)
(d) (4, 5)

Ans. b
Given
y (0) = 0



Solution of D.E.


Now, at x = 0, y = 0 ⇒ C = −2
∴ y = x (x − 2) − 4 − 2 (x − 2)
⇒ y = x2 − 4x
This curve passes through (5, 5)

Q.69. The population P = P(t) at time 't' of a certain species follows the differential equation (dP/dt) = 0.5P - 450. If P(0) = 850, then the time at which population becomes zero is :     (JEE Main 2021)
(a) log_e18
(b) (1/2)log_e18
(c) 2log_e18
(d) log_e9

Ans. c




⇒ (t/2) = ln⁡ 18
⇒ t = 2 ln⁡ 18

Q.70. If y^1/4 + y^−1/4 = 2x, and 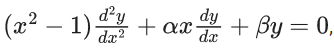 then |α − β| is equal to ______.      (JEE Main 2021)

Ans. 17










⇒ (x2−1)y″ + xy′ − 16y = 0
So, |α − β| = 17

Q.71. If y = y(x), y ∈ [0, (π/2)) is the solution of the differential equation sec⁡ y(dy/dx) − sin⁡(x+y)− sin⁡(x − y) = 0, with y(0) = 0, then 5y′(π/2) is equal to _____.     (JEE Main 2021)

Ans. 2
sec⁡ y(dy/dx) = 2sin⁡xcos⁡y
sec²ydy = 2sin ⁡x dx
tan⁡ y = −2cos⁡ x + c
c = 2
tan ⁡y = −2cos⁡x + 2 ⇒ at x = π/2
tan ⁡y = 2
sec²y(dy/dx) = 2sin⁡x
∴ 5(dy/dx) = 2

Q.72. Let F : [3, 5] → R be a twice differentiable function on (3, 5) such that 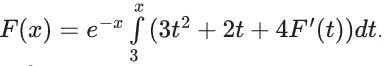 If 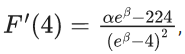 then α + β is equal to _______.      (JEE Main 2021)

Ans. 16
F(3) = 0





y.(e^x − 4) = ∫(3x² + 2x)dx + c
y(e^x − 4) = x³ + x² + c
Put x = 3 ⇒ c = −36


Now, put value of x = 4 we will get α = 12 & β = 4

Q.73. Let y = y(x) be the solution of the differential equation dy = e^{αx + y} dx; α ∈ N. If y(log_e2) = log_e2 and y(0) = log_e(1/2), then the value of α is equal to _____.      (JEE Main 2021)

Ans. 2
∫e^−ydy = ∫e^αxdx

Put (x, y) = (ln2, ln2)

Put (x, y) ≡ (0, −ln2) in (i)

(ii) − (iii)

⇒ α = 2 (as α ∈ N)

Q.74. Let y = y(x) be solution of the following differential equation  If y(0) = log_e(α+βe⁻²), then 4(α+β) is equal to ____.       (JEE Main 2021)

Ans. 4
Let e^y = t
⇒ (dt/dx) - (2sin x)t = -sin xcos²x
I.F. = e^{2cos x}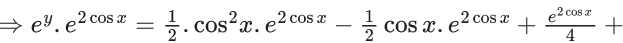


 

 


Put x = 0

Q.75. Let y = y(x) be the solution of the differential equation 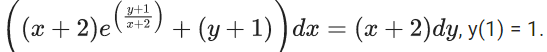 If the domain of y = y(x) is an open interval (α, β), then |α + β| is equal to _______.     (JEE Main 2021)

Ans. 4
Let y + 1 = Y and x + 2 = X
dy = dY
dx = dX





∵ (1, 1) satisfy this equation
So, c = −e^−(2/3)−ln⁡ 3
Now,
Domain :




So, α + β = −4
⇒ |α + β| = 4

Q.76. Let a curve y = y(x) be given by the solution of the differential equation 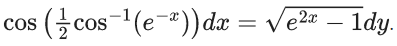 If it intersects y-axis at y = −1, and the intersection point of the curve with x-axis is (α, 0), then e^α is equal to  ______.      (JEE Main 2021)

Ans. 2















2(1 − e^−x)^1/2 = √2(y + 1), passes through (α, 0)

Q.77. Let y = y(x) be the solution of the differential equation 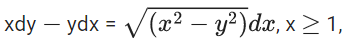 with y(1) = 0. If the area bounded by the line x = 1, x = e^π, y = 0 and y = y(x) is αe^2π + β, then the value of 10(α + β) is equal to ____.       (JEE Main 2021)

Ans. 4

dividing both sides by x², we get



Integrating both side, we get


Given, y(1) = 0 ⇒ at x = 1, y = 0
∴ ⇒sin⁻¹(0) = ln⁡(1)+C
⇒ C = 0

⇒ y = x sin(ln(x))

Let, lnx = t
⇒ x = e^t
⇒ dx = e^t dt
New lower limit, t = ln(1) = 0
and upper limit t = ln(e^π) = π







So, 10(α + β) = 4

Q.78. If y = y(x) is the solution of the equatio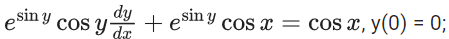n  then 

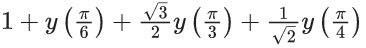 is equal to ______.        (JEE Main 2021)

Ans. 1
e^{sin y} cos y(dy/dx) + e^{sin y} cos x = cos x
Put e^{sin y} = t

I. F. = e^∫cos⁡xdx=e^sin⁡x
Solution of differential equation :
t.e^{sin⁡ x} = ∫e^{sin⁡ x}.cos⁡ x dx
e^{sin⁡ y}.e^{sin ⁡x} = e^{sin ⁡x}+c
at x = 0, y = 0
1 = 1 + c ⇒ c = 0
∴ e^{sin x + sin y} = e^{sin x}
⇒ sin x + sin y = sin x
⇒ sin y = 0 ⇒ y = 0


= 1 + 0 + 0 + 0 = 1

Q.79. The difference between degree and order of a differential equation that represents the family of curves given by 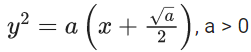 is _____.       (JEE Main 2021)

Ans. 2

Differentiating both sides, we get
2yy′ = a




D = 3 & O = 1
∴ D − O = 3 − 1 = 2

Q.80. If the curve, y = y(x) represented by the solution of the differential equation (2xy² − y)dx + xdy = 0, passes through the intersection of the lines, 2x − 3y = 1 and 3x + 2y = 8, then |y(1)| is equal to ___.      (JEE Main 2021)

Ans. 1
Given,
(2xy²−y)dx + xdx = 0


1/y = z


I. F. = e^∫(1/x)dx = x
∴ z(x) = ∫2(x)dx = x² + c
⇒ (x/y) = x² + c
As it passes through P(2, 1)
[Point of intersection of 2x − 3y = 1 and 3x + 2y = 8]
∴ (2/1) = 4 + c
⇒ c =-2
⇒ (x/y) = x² - 2
Put x = 1
(1/y) = 1 - 2 = -1
 ⇒ y(1) = -1
⇒ |y(1)| = 1