JEE Main Previous year questions (2021-23): Sequences and Series PDF Download

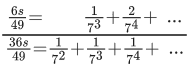
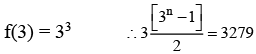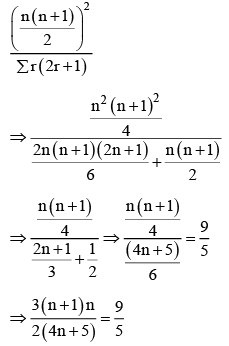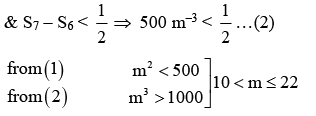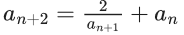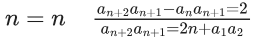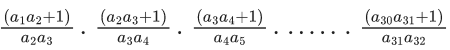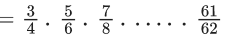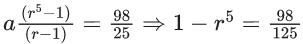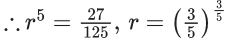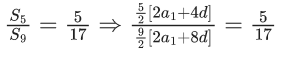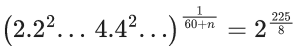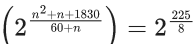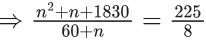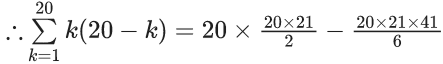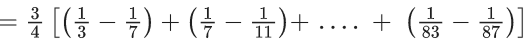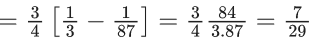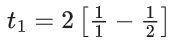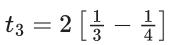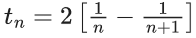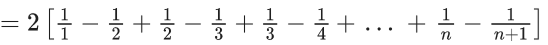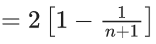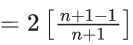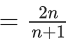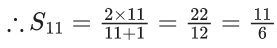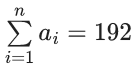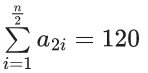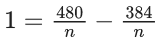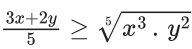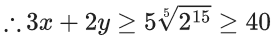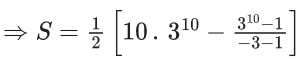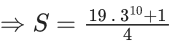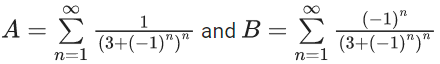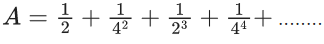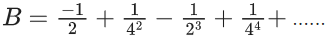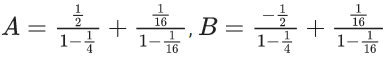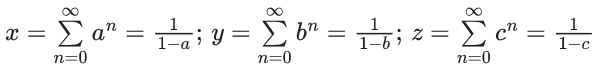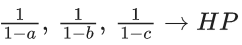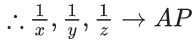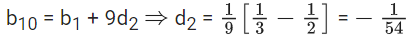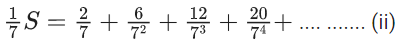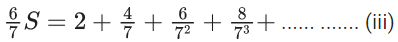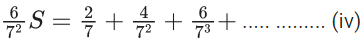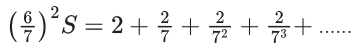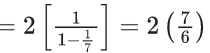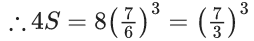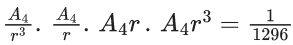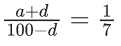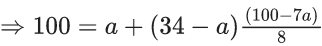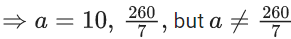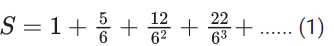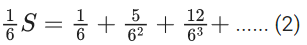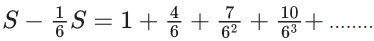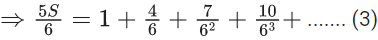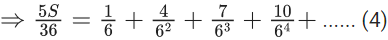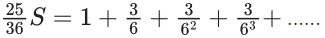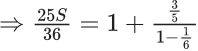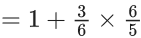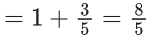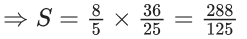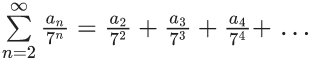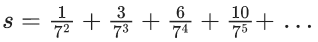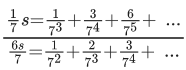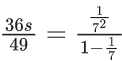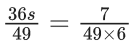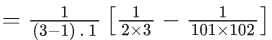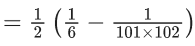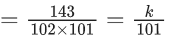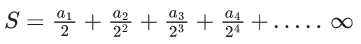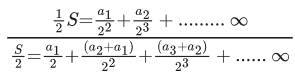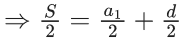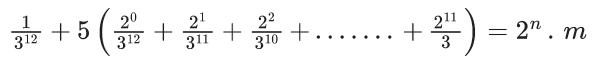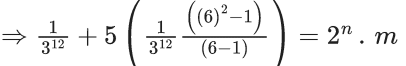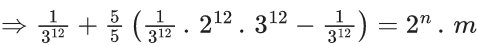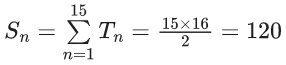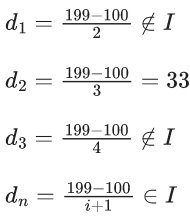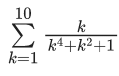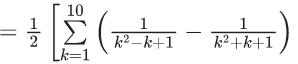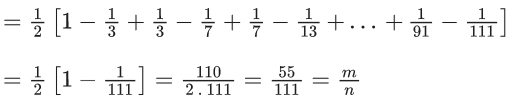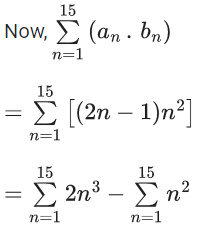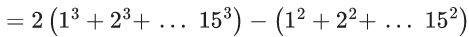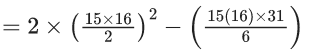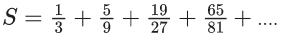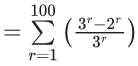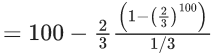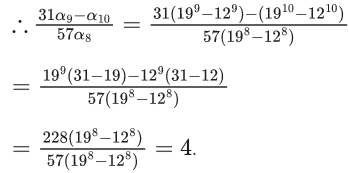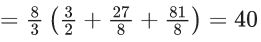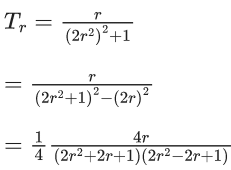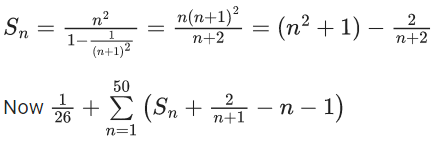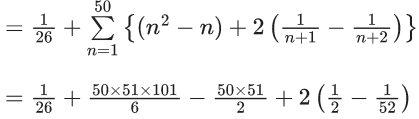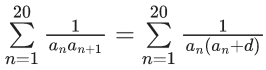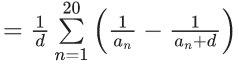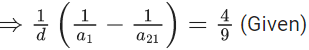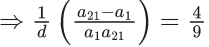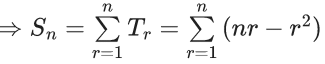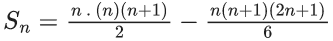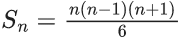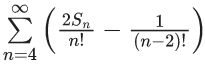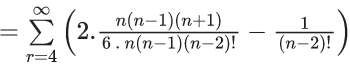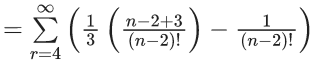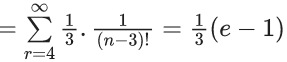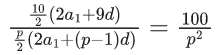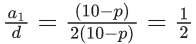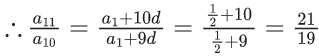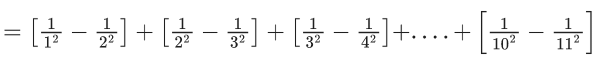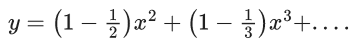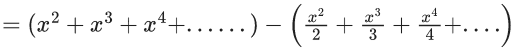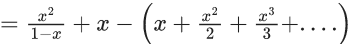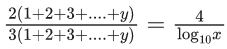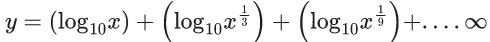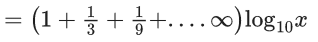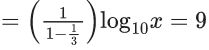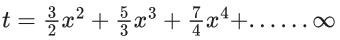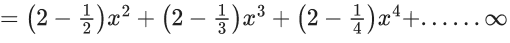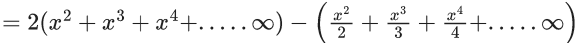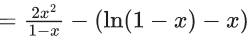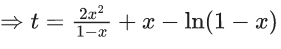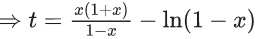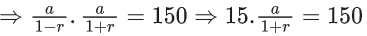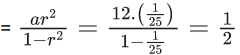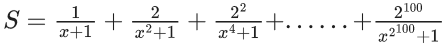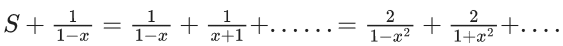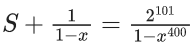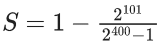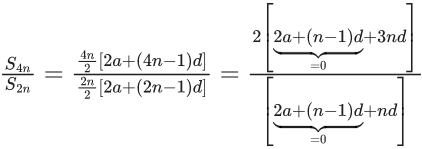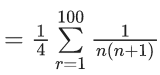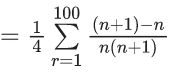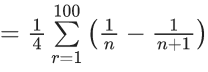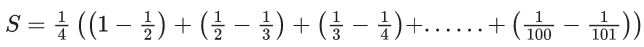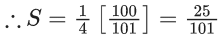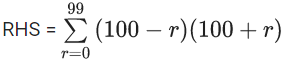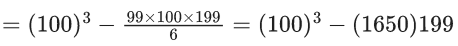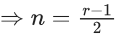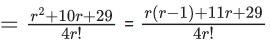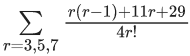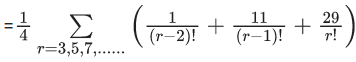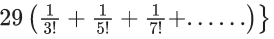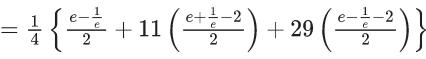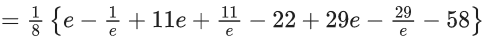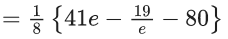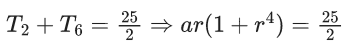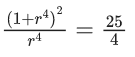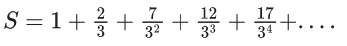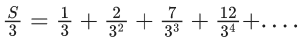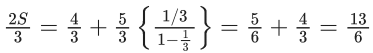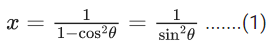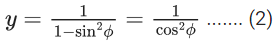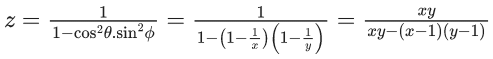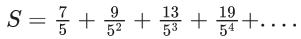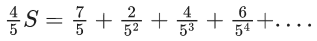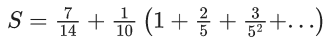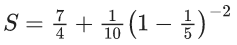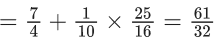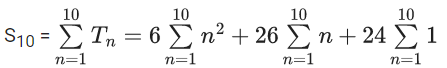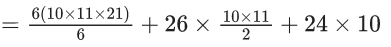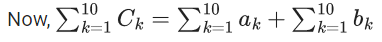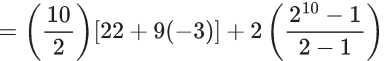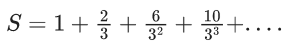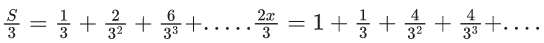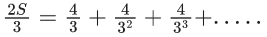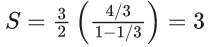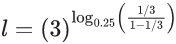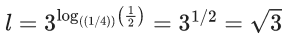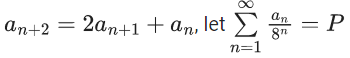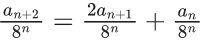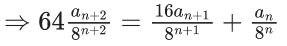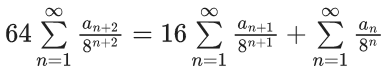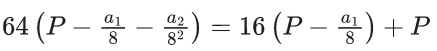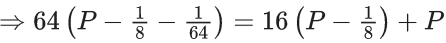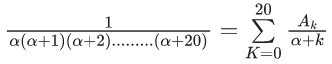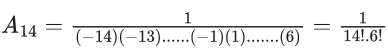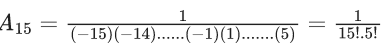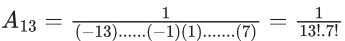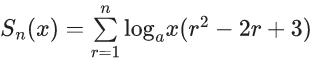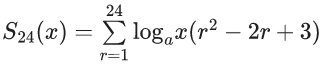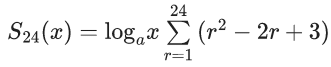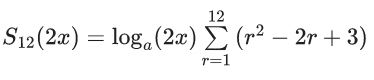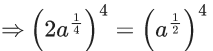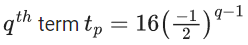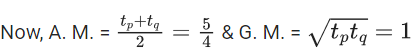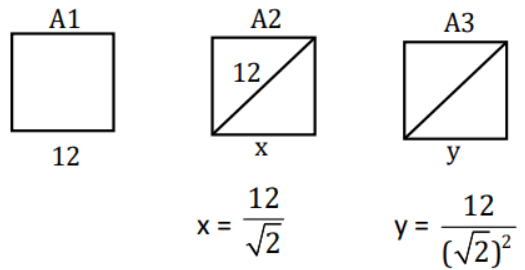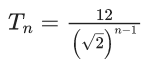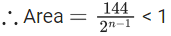Q.1. Let f(x) be a funciton such that f (x + y) = f (x) × f (y) for all x, y ∈ N . If f(1) = 3 and  = 3279, then the value of n is        (JEE Main 2023)
(a) 9
(b) 6
(c) 8
(d) 7

Ans. d
f(x +y) = f(x).f(y), x,y∈N
f(2) = 3² 

3ⁿ – 1 = 1093x2
3ⁿ - 1 = 2186
3ⁿ = 2187
n = 7

Q.2. If 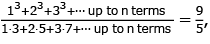 then the value of n is         (JEE Main 2023)

Ans. 5

⇒ 5n² + 5n = 24n + 30
⇒ 5n² – 19n – 30 = 0
5n² – 25n + 6n – 30 = 0
(5n + 6) (n – 5) = 0
n = 5

Q.3. The 4th term of GP is 500 and its common ratio is 1/m , m ∈ N. Let S_n denote the sum of the first n terms of this GP. If S₆ > S₅ + 1 and 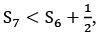 then the number of possible values of m is        (JEE Main 2023)

Ans. 12


Number of possible values of m is = 12 

Q.4. Let a₁, a₂, a₃,… be an arithmetic progression with a₁ = 7 and common difference 8. Let T₁, T₂, T₃,… be such that T₁ = 3 and T_n+1 − T_n = a_n for n ≥ 1. Then, which of the following is/are TRUE ?      (JEE Advanced 2022)
(a) T₂₀ = 1604
(b)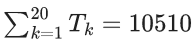
(c) T₃₀ = 3454
(d)

Ans. b and c

Q.5. Let l₁, l₂ ,…, l₁₀₀ be consecutive terms of an arithmetic progression with common difference d₁, and let w₁, w₂ ,…, w₁₀₀ be consecutive terms of another arithmetic progression with common difference d₂, where d₁d₂ = 10. For each i = 1, 2,…, 100, let R_i be a rectangle with length l_i, width w_i and area A_i. If A₅₁ − A₅₀ = 1000, then the value of A₁₀₀ − A₉₀ is _____.      (JEE Advanced 2022)

Ans. 18900
Given,
l₁, l₂,......., l₁₀₀ are in A.P with common difference d₁.
So from property of A.P we can say,
l₂ = l₁ + d₁
l₃ = l₁ + 2d₁
⋮
l₁₀₀ = l₁ + 99d₁
Also given,
w₁, w₂ ,......, w₁₀₀ are in A.P with common difference d₂.
∴ From the property of A.P we can say,
w₂ = w₁ + d₂
w₃ = w₁ + 2d₂
⋮
w₁₀₀ = w₁ + 99d₂
Now, also given,
d₁d₂ = 10
and R_i is a rectangle whose length is l_i and width is w_i and area A_i.
∴ We know, area of rectangle
A_i = l_i × w_i
∴ A₅₁ = l₅₁ × w₅₁
and A₅₀ = l₅₀ × w₅₀
Given, A₅₁ − A₅₀ = 1000
⇒ (l₁ + 50d₁)(w₁ + 50d₂)−(l₁ + 49d₁)(w₁ + 49d₂) = 1000
⇒ [l1w₁ + 2500d₁d₂ + 50(l₁d₂ + d₁w₁)] − [l₁w₁ + 49 × 49d₁d₂ + 49(l₁d₂ + w₁d₁)] = 1000
⇒ [(50)2d₁d₂ − (49)2d₁d₂] + (50−49)(l₁d₂+d₁w₁) = 1000
⇒ (99 × 1)d₁d₂ + l₁d₂ + d₁w₁ = 1000
⇒ 99 × 10 + l₁d₂ + w₁d₁ = 1000
⇒ l₁d₂ + w₁d₁ = 10
Now,
A₁₀₀ − A₉₀
= l₁₀₀.w₁₀₀ − l₉₀.w₉₀
= (l₁+99d₁)(w₁+99d₂) − (l₁ + 89d₁)(w₁ + 89d₂)
= [l₁w₁ + (99)2d₁d₂ + 99(l₁d₂ + w₁d₁)]−[l₁w₁ + (89)2d₁d₂ + 89(l₁d₂ + w₁d₁)]
= [(99)²−89²]d₁d₂ + 10(l₁d₂ + w₁d₁)
= 188 × 10 × d₁d₂ + 10×10
= 188 × 10 × 10 + 100
= 18800 + 100
= 18900

Q.6. Let 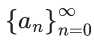 be a sequence such that a₀ = a  = 0 and a_n+1 = 3a_n+1 - 2a_n + 1, ∀n ≥ 0. Then a₂₅a₂₃ − 2a₂₅a₂₂ − 2a₂₃a₂₄ + 4a₂₂a₂₄ is equal to       (JEE Main 2022)
(a) 483
(b) 528
(c) 575
(d) 624

Ans. b
Given,
a₀ = a₁ = 0
and a_n+2 = 3a_{n + 1} − 2a_{n + 1}
For n = 0, a₂ = 3a₁ − 2a₀ + 1
= 3.0 − 2.0 + 1
= 1
For n = 1, a₃ = 3a₂ − 2a₁ + 1
= 3.1 − 2.0 + 1
= 4
For n = 2, a₄ = 3a₃−2a₂ + 1
= 3.4 − 2.1 + 1
= 11
For n = 3, a₅ = 3a₄ − 2a₃ + 1
= 3.11 − 2.4 + 1
= 26
For n = 4, a₆ = 3a₅−2a₄ + 1
= 3.26 − 2.11 + 1
= 57
∴ S_n = 1 + 4 + 11 + 26 + 57  +....+ t_n
S_n = 1 + 4 + 11 + 26 +....+ t_n−1 + t_n
0 = 1 + 3 + 7 + 15 + 31 +..... − tn
⇒ t_n = 1 + 3 + 7 + 15 + 31 +....
Now, find the sum of the series,
t_n = 1 + 3 + 7 + 15 + 31 +.....+ x_n−1 + x_n .....(1)
t_n = 1 + 3 + 7 + 15 +.....+ x_n−1 + x_n ......(2)
Subtracting (2) from (1), we get
_____________
0 = 1 + 2 + 4 + 8 + 16 +....+ x_n
⇒ x_n =1 + 2 + 4 + 8 + 16 +.....+ n terms

Q.7. Consider the sequence a₁, a₂, a₃, … such that a₁ = 1, a₂ = 2 and a_n+2 = 2/(a_n+1) + a_n for n = 1, 2, 3, …. If 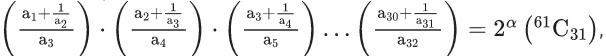 then α is equal to :     (JEE Main 2022)
(a) -30
(b) -31
(c) -60
(d) -61

Ans. c

⇒ anan+1 + 1 = a_n+1a_n+2 − 1
⇒ a_n+2 a_n+1 − a_n.a_n+1 = 2
For
n = 1 a₃a₂ − a₁a₂ = 2
n = 2 a₄a₃ − a₃a₂ =2
n = 3 a₅a₄ − a₄a₃ = 2
.
.
.
.

Now,


= 2^-60(⁶¹C₃₁)

Q.8. Let the sum of an infinite G.P., whose first term is a and the common ratio is r, be 5 . Let the sum of its first five terms be 98/25. Then the sum of the first 21 terms of an AP, whose first term is 10ar, n^th  term is a_n and the common difference is 10ar², is equal to :     (JEE Main 2022)
(a) 21 a₁₁
(b) 22 a₁₁
(c) 15 a₁₆
(d) 14 a₁₆

Ans. a
Let first term of G.P. be a and common ratio is r
Then, a/(1−r) = 5 ...... (i)


∴ Then, S₂₁ = (21/2) [2 × 10ar + 20 × 10ar²]
= 21[10ar + 10.10ar²]
= 21a₁₁

Q.9. Suppose a₁, a₂ ,…, a_n, .. be an arithmetic progression of natural numbers. If the ratio of the sum of first five terms to the sum of first nine terms of the progression is 5:17 and , 110 < a₁₅ < 120, then the sum of the first ten terms of the progression is equal to     (JEE Main 2022)
(a) 290
(b) 380
(c) 460
(d) 510

Ans. b
∵ a₁, a₂, .... a_n be an A.P of natural numbers and

⇒ 34a₁ + 68d = 18a₁ + 72d
⇒ 16a₁ = 4d
∴ d = 4a₁
And 110 < a₁₅ < 120
∴ 110 < a₁ + 14d < 120 ⇒ 110 < 57a₁ < 120
∴ a₁ =2 (∵ a_i ∈ N)
d = 8
∴ S₁₀ = 5[4 + 9 × 8] = 380

Q.10. Consider two G.Ps. 2, 2², 2³, ..... and 4, 4², 4³, .... of 60 and n terms respectively. If the geometric mean of all the 60 + n terms is (2)^(225/8), then 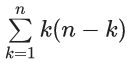 is equal to :       (JEE Main 2022)
(a) 560
(b) 1540
(c) 1330
(d) 2600

Ans. c
Given G.P's 2, 2², 2³, .... 60 terms
4, 4², .... n terms
Now, G.M = 2^(225/8)



⇒ 8n² − 217n + 1140 = 0
n = (57/8), 20, so n = 20

Q.11. The sum 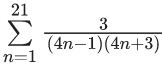 is equal to     (JEE Main 2022)
(a) 7/87
(b) 7/29
(c) 14/87
(d) 21/29

Ans. b

Q.12. The value of  is equal to:     (JEE Main 2022)
(a) 20/11
(b) 11/6
(c) 241/132
(d) 21/11

Ans. b
Given,

General term,








.
.
.

∴ S_n = t₁ + t₂ + t₃ +....+ t_n

Q.13. If 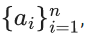 where n is an even integer, is an arithmetic progression with common difference 1, and  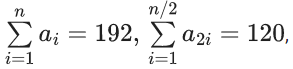then n is equal to :      (JEE Main 2022)
(a) 48
(b) 96
(c) 92
(d) 104

Ans. b

⇒ a₁ + a₂ + a₃ + ...... + a_n = 192
⇒ (n/2)[a₁+a_n] = 192
⇒ a₁ + a_n = (384/n) ..... (1)
Now,

⇒ a₂ + a₄ + a₆ + ...... + a_n = 120
Here total (n/2) terms present.

⇒ (n/4)[a₁ + 1 + a_n] = 120
⇒ a₁ + a_n + 1 = (480/n) ..... (2)
Subtracting (1) from (2), we get

⇒ 1 = (96/n)
⇒ n = 96

Q.14. Let x, y > 0. If x³y² = 2¹⁵, then the least value of 3x + 2y is     (JEE Main 2022)
(a) 30
(b) 32
(c) 36
(d) 40

Ans. d
x, y > 0 and x³y² = 2¹⁵
Now, 3x + 2y = (x + x + x) + (y + y)
So, by A.M ≥ G.M inequality


∴ Least value of 3x + 4y = 40

Q.15. If 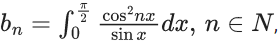 then     (JEE Main 2022)
(a) b₃−b₂, b₄−b₃, b₅−b₄ are in A.P. with common difference −2
(b) 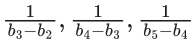  are in an A.P. with common difference 2
(c) b₃−b₂, b₄−b₃, b₅−b₄ are in a G.P.
(d) 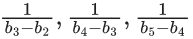 are in A.P. with common difference - 2

Ans. d



So, b₃−b₂, b₄−b₃, b₅−b₄ are in H.P.
 are in A.P. with common difference −2.

Q.16. The sum 1 + 2 . 3 + 3 . 3² + ......... + 10 . 3⁹ is equal to :     (JEE Main 2022)
(a)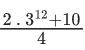
(b)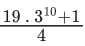
(c) 5.3¹⁰ - 2
(d)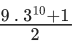

Ans. b
Let S = 1.3⁰+2.3¹+3.3²+......+10.3⁹
3S = 1.3¹ + 2.3² + .......... + 10.3¹⁰
___________________________________________________________
−2S = (1.3⁰ + 1.3¹ + 1.3² + ........ + 1.3⁹)−10.3¹⁰

Q.17. If 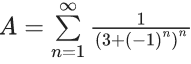 and 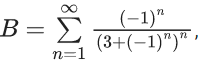 then (A/B) is equal to :     (JEE Main 2022)
(a) 11/9
(b) 1
(c) -(11/9)
(d) -(11/3)

Ans. c




A = (11/15), B = (-9)/15
∴ (A/B) = (-11)/9

Q.18. 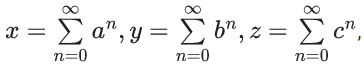 where a, b, c are in A.P. and |a| < 1, |b| < 1, |c| < 1, abc ≠ 0, then :       (JEE Main 2022)
(a) x, y, z are in A.P.
(b) x, y, z are in G.P.
(c) (1/x), (1/y), (1/z) are in A.P.
(d) (1/x) + (1/y) + (1/z) = 1 − (a + b + c)

Ans. c

Now,
a, b, c → AP
1 − a, 1 − b, 1 − c → AP

x, y, z → HP

Q.19. If a₁, a₂, a₃ ...... and b₁, b₂, b₃ ....... are A.P., and a₁ = 2, a₁₀ = 3, a₁b₁ = 1 = a₁₀b₁₀, then a₄ b₄ is equal to -     (JEE Main 2022)
(a) 35/27
(b) 1
(c) 27/28
(d) 28/27

Ans. d
a₁, a₂, a₃ .... are in A.P. (Let common difference is d₁)
b₁, b₂, b₃ .... are in A.P. (Let common difference is d₂)
and a₁ = 2, a₁₀ = 3, a₁b₁ = 1 = a₁₀b₁₀
∵ a₁b₁ = 1
∴ b₁ = 1/2
a₁₀b₁₀ = 1
∴ b₁₀ = 1/3
Now, a₁₀ = a₁ + 9d₁ ⇒ d₁ = 1/9

Now, a₄ = 2 + (3/9) = (7/3)
b₄ = (1/2) − (3/54) = (4/9)
∴ a₄b₄ = 28/27

Q.20. Let 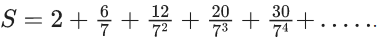 Then 4S is equal to     (JEE Main 2022)
(a) (7/3)²
(b) (7³)/(3²⁾
(c) (7/3)³
(d) (7)²/(3)³

Ans. c


(i) - (ii)


(iii) - (iv)

Q.21. Let A₁, A₂, A₃, ....... be an increasing geometric progression of positive real numbers. If A₁A₃A₅A₇ = 1/(1256) and A₂ + A₄ = (7/36), then the value of A₆ + A₈ + A₁₀ is equal to       (JEE Main 2022)
(a) 33
(b) 37
(c) 43
(d) 47

Ans. c

A₄ = 1/6
A₂ = (7/36) - (1/6) = 1/36
So A₆ + A₈ + A₁₀ = 1 + 6 + 36 = 43

Q.22. If n arithmetic means are inserted between a and 100 such that the ratio of the first mean to the last mean is 1 : 7 and a + n = 33, then the value of n is :      (JEE Main 2022)
(a) 21
(b) 22
(c) 23
(d) 24

Ans. c
a, A₁, A₂ ........... A_n, 100
Let d be the common difference of above A.P. then

⇒ 7a + 8d = 100 ...... (i)
and a + n = 33 ..... (ii)
and 100 = a + (n+1)d

⇒ 800 = 8a + 7a² - 338a + 3400
⇒ 7a² - 330a + 2600 = 0

∴ n = 23

Q.23. The sum of the infinite series 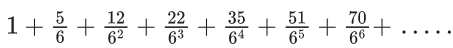  is equal to :     (JEE Main 2022)
(a) 425/216
(b) 429/216
(c) 288/125
(d) 280/125

Ans. c




Now, multiplying both sides by (1/6), we get

Subtract equation (4) from equation (3), we get

Q.24. Let 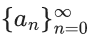 be a sequence such that a₀ = a₁ = 0 and a_n+2 = 2a_n+1 − a_n+1 for all n ≥ 0. Then,  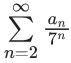is equal to:      (JEE Main 2022)
(a) 6/343
(b) 7/216
(c) 8/343
(d) 49/216

Ans. b
a_n+2 = 2a_{n + 1} − a_n + 1 & a₀ = a₁ = 0
a₂ = 2a₁ − a₀ + 1 = 1
a₃ = 2a₂ − a₁ + 1 = 3
a₄ = 2a₃ − a₂ + 1 = 6
a₅ = 2a₄ − a₃ + 1 = 10

s = 7/216

Q.25. If 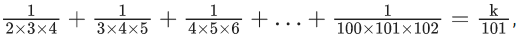 then 34 k is equal to _____.      (JEE Main 2022)

Ans. 286




∴ 34k = 286.

Q.26. Let a₁, a₂, a₃, … be an A.P. If 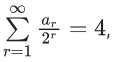 then 4a₂ is equal to ____.     (JEE Main 2022)

Ans. 16
Given



⇒ a₁ + d = a₂ = 4 ⇒ 4a₂ = 16

Q.27. 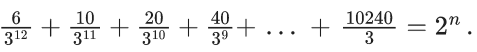m, where m is odd, then m . n is equal to ______.       (JEE Main 2022)

Ans. 12




⇒ 2ⁿ.m = 2¹²
⇒ m = 1 and n = 12
m . n = 12

Q.28. 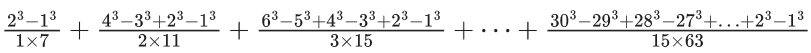 is equal to ________.       (JEE Main 2022)

Ans. 120



∴ T_n = n

Q.29. Different A.P.'s are constructed with the first term 100, the last term 199, and integral common differences. The sum of the common differences of all such A.P.'s having at least 3 terms and at most 33 terms is ____.       (JEE Main 2022)

Ans. 53

di = 33 + 11, 9
Sum of CD's = 33 + 11 + 9
= 53

Q.30. If 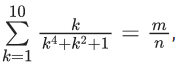 where m and n are co-prime, then m + n is equal to _____.    (JEE Main 2022)

Ans. 166



∴ m + n = 55 + 111 = 166

Q.31. The series of positive multiples of 3 is divided into sets : {3}, {6, 9, 12}, {15, 18, 21, 24, 27}, … Then the sum of the elements in the 11^th  set is equal to _____.     (JEE Main 2022)

Ans. 6993
Given series

∴ 11^th set will have 1+(10)2 = 21 term
Also upto 10^th set total 3 × k type terms will be 1 + 3 + 5 +......+ 19 = 100 − term
∴ Set 11= {3 × 101, 3 × 102 ,...... 3 × 121}
∴ Sum of elements = 3 × (101 + 102 +...+ 121)
= (3 × 222 × 21)/2 = 6993

Q.32. Let a₁ = b₁ = 1, a_n = a_n−1 + 2 and b_n = a_n + b_n−1 for every natural number n ⩾ 2. Then 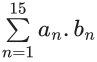 is equal to _____.        (JEE Main 2022)

Ans. 27560
Given,
a_n = a_n−1 + 2
⇒a_n − a_n−1 = 2
∴ In this series between any two consecutives terms difference is 2. So this is an A.P. with common difference 2.
Also given a₁ = 1
∴ Series is = 1, 3, 5, 7 ......
∴ a_n = 1+(n−1)2 = 2n−1
Also b_n = a_n + b_n−1
When n = 2 then
b₂−b₁ = a₂ = 3
⇒ b₂−1 = 3 [Given b₁ = 1]
⇒ b₂ = 4
When n = 3 then
b₃ − b₂ = a₃
⇒ b₃ − 4 = 5
⇒ b₃ = 9
∴ Series is = 1, 4, 9 ......
= 1², 2², 3² ....... n²
∴ b_n = n²



= 27560

Q.33. Let a, b be two non-zero real numbers. If p and r are the roots of the equation x² − 8ax + 2a = 0 and q and s are the roots of the equation x² + 12 bx + 6 b = 0, such that (1/p), (1/q), (1/r), (1/s) are in A.P., then a⁻¹−b⁻¹ is equal to _______.      (JEE Main 2022)

Ans. 38
∵ Roots of 2ax² − 8ax + 1 = 0 are (1/p) and (1/r) and roots of 6bx² + 12bx + 1 = 0 are 1/q and 1/s.
Let (1/p), (1/q), (1/r), (1/s) as α−3β, α−β, α+β, α+3β
So sum of roots 2α − 2β = 4 and 2α + 2β = −2
Clearly α = (1/2) and β = −(3/2)
Now product of roots, 1/p⋅1/r = 1/2a = −5 ⇒ 1/a = −10
and 1/q⋅1/x = 1/6b = −8 ⇒ 1/b = −48
So, (1/a) - (1/b) = 38

Q.34. The greatest integer less than or equal to the sum of first 100 terms of the sequence 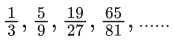 is equal to _____.      (JEE Main 2022)

Ans. 98



= 98 + 2(2/3)¹⁰⁰
∴ [S] = 98

Q.35. For a natural number n, let α_n = 19ⁿ − 12ⁿ. Then, the value of 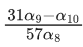 is ____.       (JEE Main 2022)

Ans. 4
αn = 19ⁿ−12ⁿ
Let equation of roots 12 & 19 i.e.
x² − 31x + 228 = 0
⇒ (31 − x) = (228/x) (where x can be 19 or 12)

Q.36. If a₁ (> 0), a₂, a₃, a₄, a₅ are in a G.P., a₂ + a₄ = 2a₃ + 1 and 3a₂ + a₃ = 2a₄, then a₂ + a₄ + 2a₅ is equal to ____.     (JEE Main 2022)

Ans. 40
Let G.P. be a₁ = a, a₂ = ar, a₃ = ar², .........
∵ 3a₂ + a₃ = 2a₄
⇒ 3ar + ar² = 2ar³
⇒ 2ar² − r − 3 = 0
∴ r = −1 or (3/2)
∵ a₁ = a > 0 then r ≠ −1
Now, a₂ + a₄ = 2a₃ + 1
ar + ar³ = 2ar² + 1
a((3/2) + (27/8) − (9/2)) = 1
∴ a = 8/3
∴ a₂ + a₄ + 2a₅ = a(r + r³ + 2r⁴)

Q.37. If the sum of the first ten terms of the series 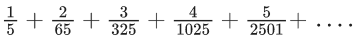 is (m/n), where m and n are co-prime numbers, then m + n is equal to ______.      (JEE Main 2022)

Ans. 276


∴ m + n = 276

Q.38. Let for n = 1, 2, ......, 50, S_n be the sum of the infinite geometric progression whose first term is n² and whose common ratio is 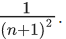 Then the value of  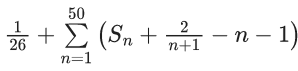is equal to _____.      (JEE Main 2022)

Ans. 41651


= 1 + 25 × 17(101 − 3)
= 41651

Q.39. Let 3, 6, 9, 12, ....... upto 78 terms and 5, 9, 13, 17, ...... upto 59 terms be two series. Then, the sum of the terms common to both the series is equal to ______.       (JEE Main 2022)

Ans. 2223
1st AP :
3, 6, 9, 12, ....... upto 78 terms
t₇₈ = 3 + (78 − 1)3
= 3 + 77 × 3
= 234
2nd AP :
5, 9, 13, 17, ...... upto 59 terms
t₅₉ = 5 + (59 − 1)4
= 5 + 58 × 4
= 237
Common term's AP :
First term = 9
Common difference of first AP = 3
And common difference of second AP = 4
∴ Common difference of common terms
AP = LCM (3, 4) = 12
∴ New AP = 9, 21, 33, .......
t_n = 9 + (n − 1)12 ≤ 234
⇒ n ≤ (237/12)
⇒ n = 19
∴ S₁₉ = (19/2)[2.9+(19−1)12]
= 19(9+108)
= 2223

Q.40. Let a₁, a₂, ____, a₂₁ be an AP such that 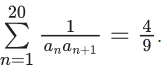 If the sum of this AP is 189, then a₆a₁₆ is equal to :     (JEE Main 2021)
(a) 57
(b) 72
(c) 48
(d) 36

Ans. b




 ⇒ a₁a₂ = 45 .... (1)
Now sum of first 21 terms = (21/2)(2a₁ + 20d) = 189
⇒ a₁ + 10d = 9 ..... (2)
For equation (1) & (2) we get
a₁ = 3 & d =(3/5)
or a₁ = 15 & d =-(3/5)
So, a₆ . a₁₆ = (a₁ + 5d) (a₁ + 15d)
⇒ a₆a₁₆ = 72
Option (b)

Q.41. Let S_n = 1 . (n − 1) + 2 . (n − 2) + 3 . (n − 3) + ..... + (n − 1) . 1, n ≥ 4.
The sum 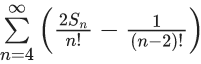 is equal to :     (JEE Main 2021)
(a) (e-1)/3
(b) (e-2)/6
(c) e/3
(d) e/6

Ans. a
Let T_r = r(n − r)
T_r = nr − r²



Now,



Option (a)

Q.42. Let a₁, a₂, a₃, ..... be an A.P. If 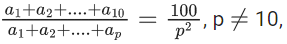 then (a₁₁/a₁₀) is equal to :      (JEE Main 2021)
(a) 19/21
(b) 100/121
(c) 21/19
(d) 121/100

Ans. c

(2a₁+9d)p = 10(2a₁ + (p−1)d)
9dp = 20a₁ − 2pa₁ + 10d(p−1)
9p = (20−2p)(a₁/d) + 10(p−1)

Q.43. Three numbers are in an increasing geometric progression with common ratio r. If the middle number is doubled, then the new numbers are in an arithmetic progression with common difference d. If the fourth term of GP is 3 r², then r² − d is equal to :     (JEE Main 2021)
(a) 7 - 7√3
(b) 7 + √3
(c) 7 - √3
(d) 7 + 3√3

Ans. b
Let numbers be (a/r), a, ar → G.P.
(a/r), 2a, ar → A.P. ⇒ 4a = (a/r) + ar ⇒ r + (1/r) = 4
r = 2 ± √3
4^th form of G.P. = 3r² ⇒ ar² = 3r² ⇒ a = 3

r² − d = (2 + √3)² − 3√3
= 7 + 4√3 − 3√3
= 7 + √3

Q.44. The sum of 10 terms of the series 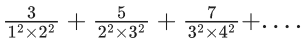 is :     (JEE Main 2021)
(a) 1
(b) 120/121
(c) 99/100
(d) 143/144

Ans. b


= 1 - (1/121)
= 120/121

Q.45. If 0 < x < 1 and 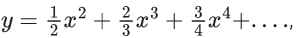 then the value of e^1+y at x = 1/2 is :     (JEE Main 2021)
(a) (1/2)e²
(b) 2e
(c) (1/2)√e
(d) 2e²

Ans. a




x = (1/2) ⇒ y = 1 − ln⁡²
e^1+y = e^1+1−ln⁡2
= e^{2-In 2} = e²/2

Q.46. If for x, y ∈ R, x > 0, y = log₁₀x + log₁₀x^1/3 + log₁₀x^1/9 + ...... upto ∞ terms and 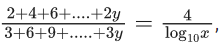 then the ordered pair (x, y) is equal to :       (JEE Main 2021)
(a) (10⁶, 6)
(b) (10⁴, 6)
(c) (10², 3)
(d) (10⁶, 9)

Ans. d

⇒ log₁₀x = 6 ⇒ x = 10⁶
Now,



So, (x, y) = (10⁶, 9)

Q.47. If 0 < x < 1, then  is equal to :        (JEE Main 2021)
(a)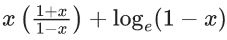
(b)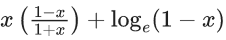
(c)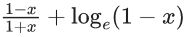
(d)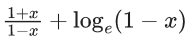

Ans. a
Let

Q.48. If the sum of an infinite GP a, ar, ar², ar³, ....... is 15 and the sum of the squares of its each term is 150, then the sum of ar², ar⁴, ar⁶, ....... is :     (JEE Main 2021)
(a) 5/2
(b) 1/2
(c) 25/2
(d) 9/2

Ans. b
Sum of infinite terms :
a/(1−r) = 15 ..... (i)
Series formed by square of terms :
a², a²r², a²r⁴, a²r⁶ .......
Sum = a²/(1 − (r²)) = 150

⇒ (a)/(1+r) = 10 ....(ii)
by (i) and (ii), a = 12; r = (1/5)
Now, series : ar², ar⁴, ar⁶
Sum

Q.49. The sum of the series 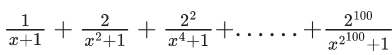 when x = 2 is :     (JEE Main 2021)
(a)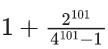
(b)
(c)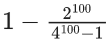
(d)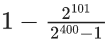

Ans. d

Q.50. Let S_n be the sum of the first n terms of an arithmetic progression. If S_3n = 3S_2n, then the value of S_4n/S_2n is :     (JEE Main 2021)
(a) 6
(b) 4
(c) 2
(d) 8

Ans. a
Let a be first term and d be common diff. of this A.P.
Given, S_3n = 3S_2n
⇒ (3n/2)[2a + (3n−1)d] = 3(2n/2)[2a + (2n−1)d]
⇒ 2a + (3n−1)d = 4a + (4n−2)d
⇒ 2a + (n−1)d = 0
Now,

= 6nd/nd =6

Q.51. Let S_n denote the sum of first n-terms of an arithmetic progression. If S₁₀ = 530, S₅ = 140, then S₂₀ − S₆ is equal to:       (JEE Main 2021)
(a) 1862
(b) 1842
(c) 1852
(d) 1872

Ans. a
Let first term of A.P. be a and common difference is d.
∴ S₁₀ = (10/2){2a + 9d} = 530
∴ 2a + 9d = 106 ..... (i)
S₅ = (5/2){2a+4d}=140
a + 2d = 28 ...... (ii)
From equation (i) and (ii), a = 8, d = 10
∴ S₂₀−S₆ = (20/2){2 × 8 + 19 × 10} − (6/2){2 × 8 + 5 × 10}
= 2060 − 198 = 1862

Q.52. If sum of the first 21 terms of the series 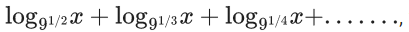 where x > 0 is 504, then x is equal to       (JEE Main 2021)
(a) 243
(b) 9
(c) 7
(d) 81

Ans. d
s = 2log₉x + 3log₉x +.......+ 22log₉x
s = log₉x(2 + 3 +.....+ 22)
s = log₉x{(21/2)(2 + 22)}
Given, 252log₉x = 504
⇒ log₉x = 2 ⇒ x = 81

Q.53. Let S₁ be the sum of first 2n terms of an arithmetic progression. Let S2 be the sum of first 4n terms of the same arithmetic progression. If (S₂ − S₁) is 1000, then the sum of the first 6n terms of the arithmetic progression is equal to :      (JEE Main 2021)
(a) 7000
(b) 1000
(c) 3000
(d) 5000

Ans. c
S₁ = 2n/2[2a + (2n − 1)d]
S₂ = 4n/2[2a + (4n − 1)d]
(where a = T₁ and d is common difference)
S₂ − S₁ ⇒ 2n[2a + (4n − 1)d] − n[2a + (2n − 1)d] = 1000
⇒ n[2a + d(8n − 2 − 2n + 1)] = 1000
⇒ n[2a + (6n − 1)d] = 1000
S₆ = (6n/2)[2a + (6n − 1)d] = 3(S₂ − S₁) = 3000

Q.54. 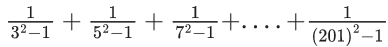 is equal to       (JEE Main 2021)
(a) 101/404
(b) 25/101
(c) 101/408
(d) 99/400

Ans. b

Q.55. If α, β are natural numbers such that 100^α − 199β = (100)(100) + (99)(101) + (98)(102) + ...... + (1)(199), then the slope of the line passing through (α, β) and origin is :         (JEE Main 2021)
(a) 540
(b) 550
(c) 530
(d) 510

Ans. b


LHS = (100)^α − (199)^β
So, α = 3, β = 1650
Slope = tanθ = (β/α)
⇒ tanθ = 550

Q.56. The sum of the series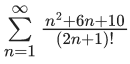
 is equal to :      (JEE Main 2021)
(a)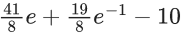
(b)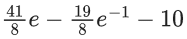
(c)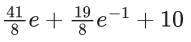
(d)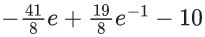

Ans. b

Put 2n + 1 = r, where r = 3, 5, 7, .......



Now,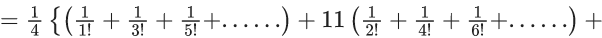

 

Q.57. In an increasing geometric series, the sum of the second and the sixth term is (25/2) and the product of the third and fifth term is 25. Then, the sum of 4^th, 6^th and 8^th terms is equal to :      (JEE Main 2021)
(a) 30
(b) 32
(c) 26
(d) 35

Ans. d
a, ar, ar², .....

a²r²(1+r⁴)² = (625/4) .... (1)
T₃.T₅ = 25 ⇒ (ar²)(ar⁴) = 25
a²r⁶ = 25 .....(2)
On dividing (1) by (2)

4r⁸ − 14r⁴ + 4 = 0
(4r⁴ − 1)(r⁴ − 4) = 0
r⁴ = (1/4), 4 ⇒ r⁴ = 4 (an increasing geometric series)
a²r⁶ = 25 ⇒ (ar³)² = 25
T₄ + T₆ + T₈ = ar³ + ar⁵ + ar⁷
= ar³(1 + r² +r⁴)
= 5(1 + 2 + 4) = 35

Q.58. The sum of the infinite series 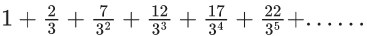is equal to :     (JEE Main 2021)
(a) 9/4
(b) 13/4
(c) 15/4
(d) 11/4

Ans. b


 up to infinite terms

⇒ S = (13/4)

Q.59. If 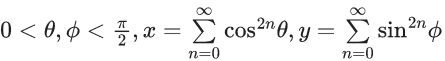 and 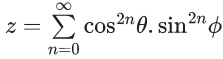 then :     (JEE Main 2021)
(a) xy − z = (x + y)z
(b) xyz = 4
(c) xy + z = (x + y)z
(d) xy + yz + zx = z

Ans. c

x = 1 + cos²θ +.......... ∞

y = 1 + sin²ϕ +........ ∞


⇒ xz + yz − z = xy
⇒ xy + z = (x+y)z

Q.60. If 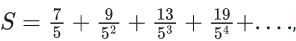  then 160 S is equal to ________.       (JEE Main 2021)

Ans. 305


On subtracting




⇒ 160S = 5 × 61 = 305

Q.61. The mean of 10 numbers 7 × 8, 10 × 10, 13 × 12, 16 × 14, ....... is _____.       (JEE Main 2021)

Ans. 398
7 × 8, 10 × 10, 13 × 12, 16 × 14 ........
Tn = (3n + 4) (2n + 6) = 2(3n + 4) (n + 3)
= 2(3n² + 13n + 12) = 6n² + 26n + 24


= 10 × 11(21 + 13) + 240
= 3980
Mean = (S₁₀/10) = 3980/10 = 398.

Q.62. Let a₁, a₂, ......., a₁₀ be an AP with common difference − 3 and b₁, b₂, ........., b₁₀ be a GP with common ratio 2. Let c_k = a_k + b_k, k = 1, 2, ......, 10. If c₂ = 12 and c₃ = 13, then 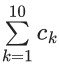 is equal to ____.      (JEE Main 2021)

Ans. 2021
a₁, a₂, a₃ ,…, a₁₀ are in AP common difference = −3
b₁, b₂, b₃ ,…, b₁₀ are in GP common ratio = 2
Since, c_k = a_k + b_k, k = 1, 2, 3 ……,10
∴ c₂ = a₂ + b₂ = 12
c₃ = a₃ + b₃ = 13
Now, C₃ − C₂ = 1
⇒ (a₃ − a₂) + (b₃ − b₂) ≠ 1 ⇒ −3+(2b₂ − b₂) ≠ 1
⇒  b₂ = 4
∴ a₂ = 8
So, AP is 11, 8, 5,….


= 5(22−27) + 2(1023) = 2046 − 25
= 2021

Q.63. The sum of all 3-digit numbers less than or equal to 500, that are formed without using the digit "1" and they all are multiple of 11, is _____.      (JEE Main 2021)

Ans. 7744
209, 220, 231, ..........., 495
Sum = (27/2)(209 + 495) = 9504
Number containing 1 at unit place

Number containing 1 at 10^th place

Required = 9504 − (231 + 341 + 451 + 319 + 418)
= 7744

Q.64. If log₃2, log₃(2^x−5), log₃(2^x− (7/2)) are in an arithmetic progression, then the value of x is equal to ______.      (JEE Main 2021)

Ans. 3
2log₃(2^x − 5) = log₂ + log₃(2^x − (7/2))
Let 2_x = t
log₃(t−5)² = log₃2(t − (7/2))
(t−5)² = 2t−7
t² − 12t + 32 = 0
(t − 4)(t − 8) = 0
⇒ 2^x = 4 or 2^x = 8
x = 2 (Rejected)
Or x = 3

Q.65. If the value of 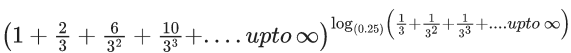 is l, then l² is equal to ______.        (JEE Main 2021)

Ans. 3





Now,

⇒ l² = 3

Q.66. The sum of all the elements in the set {n ∈ {1, 2, ....., 100} | H.C.F. of n and 2040 is 1} is equal to _____.       (JEE Main 2021)

Ans. 1251
2040 = 2³ × 3 × 5 × 17
n should not be multiple of 2, 3, 5 and 17.
Sum of all n = (1 + 3 + 5 + ...... + 99) − (3 + 9 + 15 + 21 + ...... + 99) − (5 + 25 + 35 + 55 + 65 + 85 + 95) − (17)
= 2500 − (17/2)(3 + 99) − 365 − 17
2500 − 867 − 365 − 17
= 1251

Q.67. Let 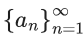 be a sequence such that a₁ = 1, a₂ = 1 and a_n+2 = 2a_n+1 + a_n for all n ≥ 1. Then the value of  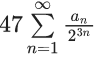is equal to ____.      (JEE Main 2021)

Ans. 7

Divide by 8ⁿ we get





64P − 8 − 1 = 16P − 2 + P
47P = 7

Q.68. For k ∈ N, let 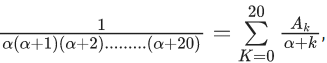 where α > 0. Then the value of  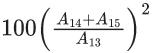     is equal to ______.      (JEE Main 2021)

Ans. 9

Q.69. Let (1/16), a and b be in G.P. and (1/a), (1/b), 6 be in A.P., where a, b > 0. Then 72(a + b) is equal to _____.         (JEE Main 2021)

Ans. 14

Solving, we get a = (1/12) or a = −(1/4) [rejected]
if a = (1/12) ⇒ b = (1/9)
∴ 72(a + b) =72((1/12) + (1/9)) = 14

Q.70. S_n(x) = log_a^1/2x + log_a^1/3x + log_a^1/6x + log_a^1/11x + log_a^1/18x + log_a^1/27x + ...... up to n-terms, where a > 1. If S₂₄(x) = 1093 and S₁₂(2x) = 265, then value of a is equal to _______.       (JEE Main 2021)

Ans. 16
S_n(x) = log_ax² + log_ax³ + log_ax⁶ + log_ax¹¹
S_n(x) = 2log_ax + 3log_ax + 6log_ax + 11log_ax + ......
S_n(x) = log_ax(2 + 3 + 6 + 11 +.....)
S_r = 2 + 3 + 6 + 11
∴ T_n = 2 + (1 + 3 + 5 +......+ (n - 1))
= 2 + ((n−1)/2)[2.1+(n−2)2]
= 2 + (n−1)[1+(n−2)]
= n² - 2n + 3
General term T_r = r² − 2r + 3



1093 = 4372log_ax
log_ax =1/4
x = a^1/4 .....(i)

265 = 530log_a(2x)
log_a(2x) = 1/2
2x = a^1/2 ....(ii)
From (i) and (ii), we get
2a^1/4 = a^1/2

⇒ 16a = a²
⇒ a = 16

Q.71. Consider an arithmetic series and a geometric series having four initial terms from the set {11, 8, 21, 16, 26, 32, 4}. If the last terms of these series are the maximum possible four digit numbers, then the number of common terms in these two series is equal to ____.      (JEE Main 2021)

Ans. 3
A.P. from the set will be 11, 16, 21, 26 .....
G.P. from the set will be 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192 .....
So common terms are 16, 256, 4096.

Q.72. If the arithmetic mean and geometric mean of the p^th and q^th terms of the sequence −16, 8, −4, 2, ...... satisfy the equation 4x² − 9x + 5 = 0, then p + q is equal to ____.     (JEE Main 2021)

Ans. 10
Given, 4x² − 9x + 5 = 0
⇒ (x−1)(4x−5) = 0
⇒  A. M. = (5/4), G. M. = 1 (As A. M. ≥ G. M)
Again, for the series
−16, 8, −4, 2 ..........



⇒ 16²(−(1/2))^(p+q−2) = 1
⇒ (−2)⁸ = (−2)^(p+q−2)
⇒ p + q = 10

Q.73. The total number of 4-digit numbers whose greatest common divisor with 18 is 3, is _________.     (JEE Main 2021)

Ans. 1000
Let N be the four digit number
gcd(N, 18) = 3
Hence N is an odd integer which is divisible by 3 but not by 9.
4 digit odd multiples of 3
1005, 1011, ..........., 9999 → 1500
4 digit odd multiples of 9
1017, 1035, ..........., 9999  → 500
Hence number of such N = 1000

Q.74. Let A₁, A₂, A₃, ....... be squares such that for each n ≥ 1, the length of the side of A_n equals the length of diagonal of A_n+1. If the length of A₁ is 12 cm, then the smallest value of n for which area of A_n is less than one, is ______.       (JEE Main 2021)

Ans. 9

∴ Side lengths are in G.P.


⇒ 2^{n − 1} > 144
Smallest n = 9.