JEE Main Previous year questions (2021-23): Probability PDF Download

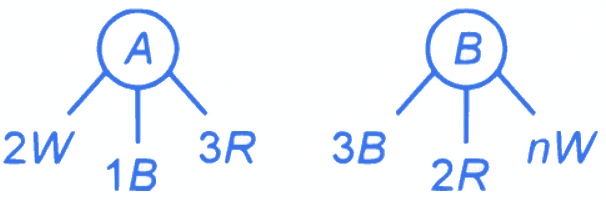
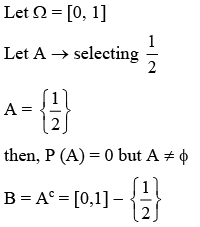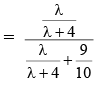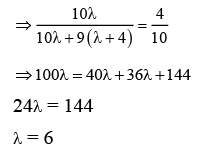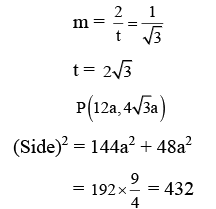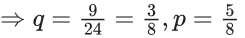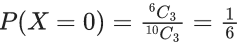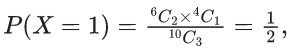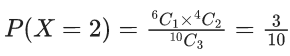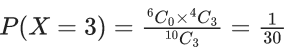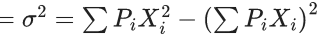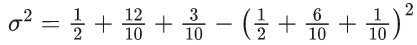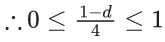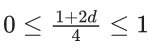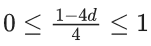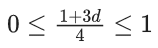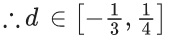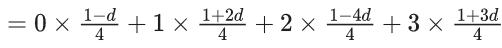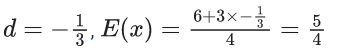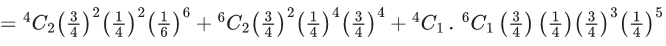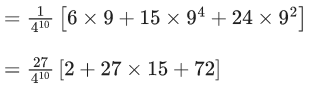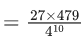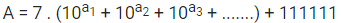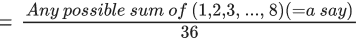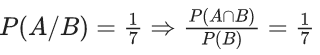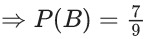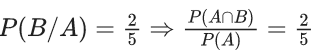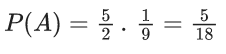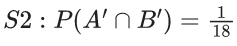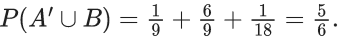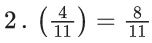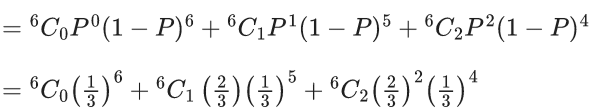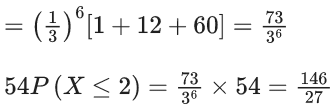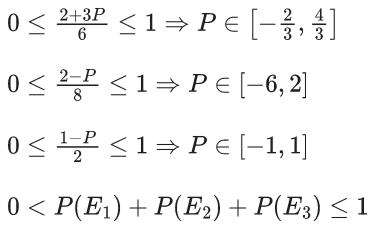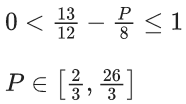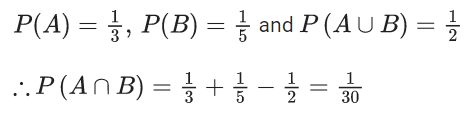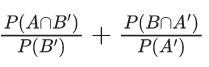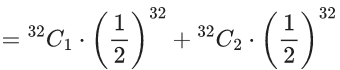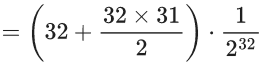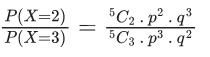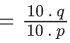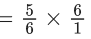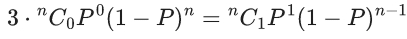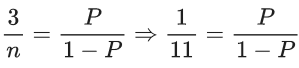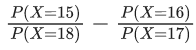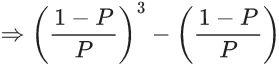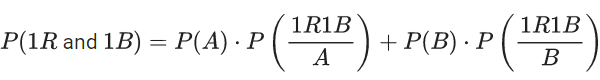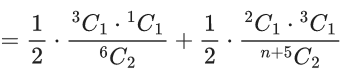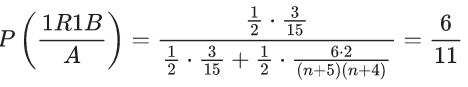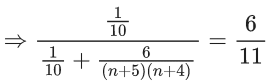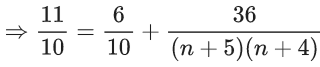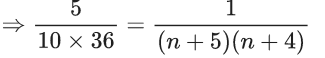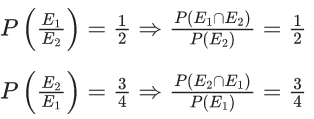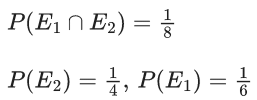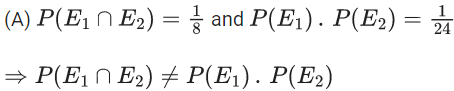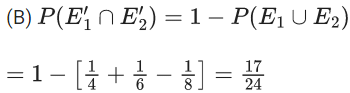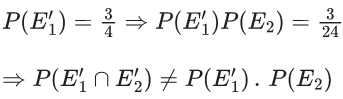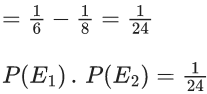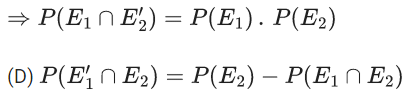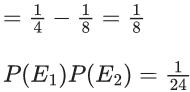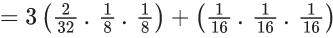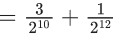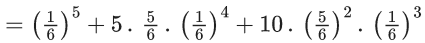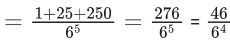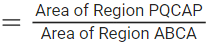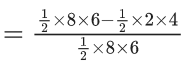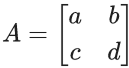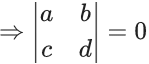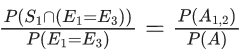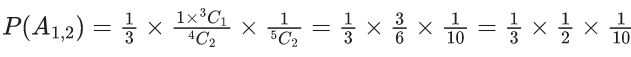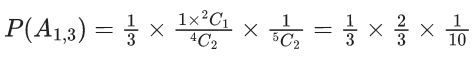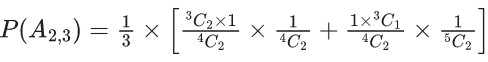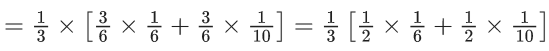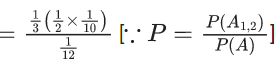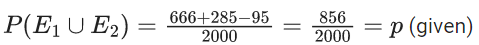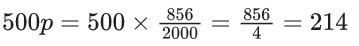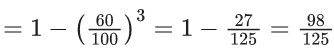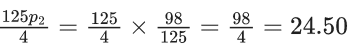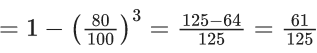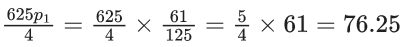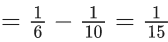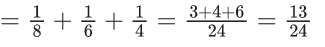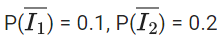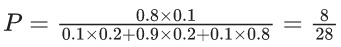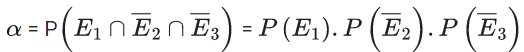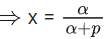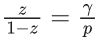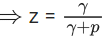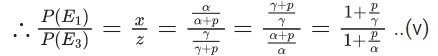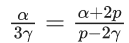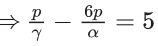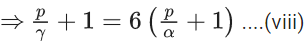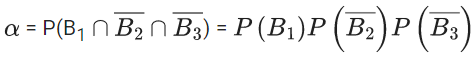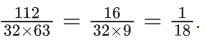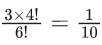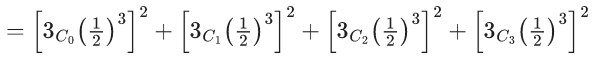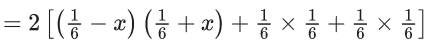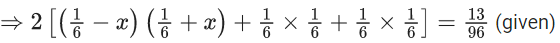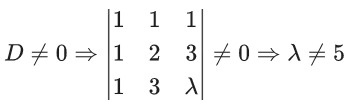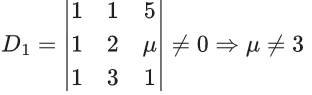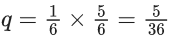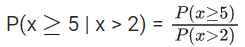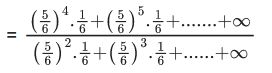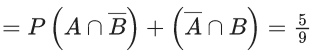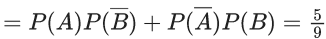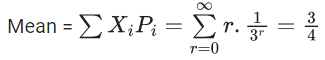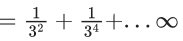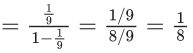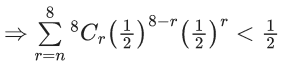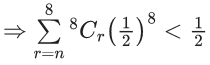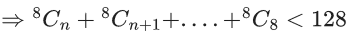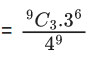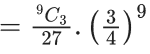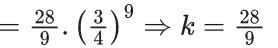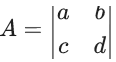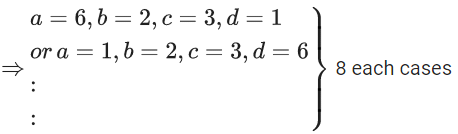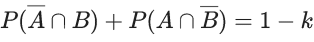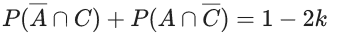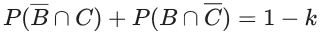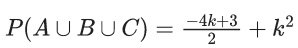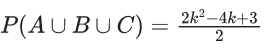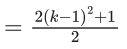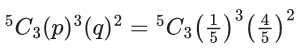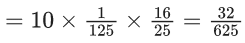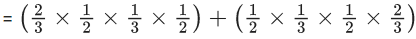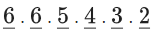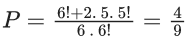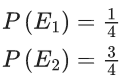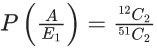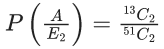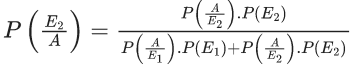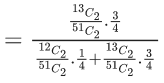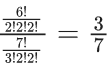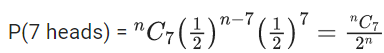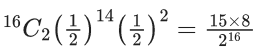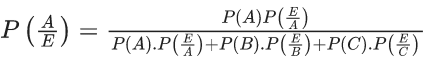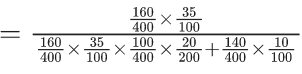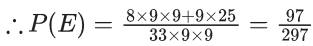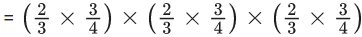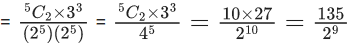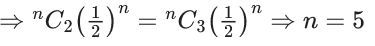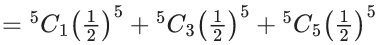Q.1. Let Ω be the sample space and  A ⊆ Ω be an event.        (JEE Main 2023)
Given below are two statements :
(S1) : If P(A⁢) = 0, then ⁢A = ∅
(S2): If P(A) = 1, then A = Ω
Then
(a) both (S₁) and (S₂) are true
(b) only (S₁) is true
(c) only (S₂) is true
(d) both (S₁) and (S₂) are false

Ans. d

P(B) = 1
but B ≠ Ω

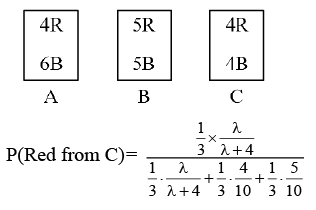
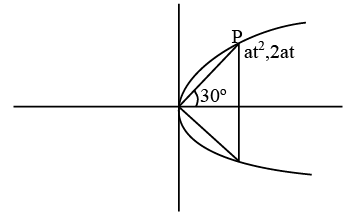
Q.2. Three urns A, B and C contain 4 red, 6 black; 5 red, 5 black; and λ red, 4 black balls respectively. One of the urns is selected at random and a ball is drawn. If the ball drawn is red and the probability that it is drawn from urn C is 0.4 then the square of the length of the side of the largest equilateral triangle, inscribed in the parabola y² = λx with one vertex at the vertex of the parabola, is         (JEE Main 2023)

Ans. 432

Q.3. Suppose that
Box-I contains 8 red, 3 blue and 5 green balls,
Box-II contains 24 red, 9 blue and 15 green balls,
Box-III contains 1 blue, 12 green and 3 yellow balls,
Box-IV contains 10 green, 16 orange and 6 white balls.
A ball is chosen randomly from Box-I; call this ball b. If b is red then a ball is chosen randomly from Box-II, if b is blue then a ball is chosen randomly from Box-III, and if b is green then a ball is chosen randomly from Box-IV. The conditional probability of the event 'one of the chosen balls is white' given that the event 'at least one of the chosen balls is green' has happened, is equal to     (JEE Advanced 2022)
(a) 15/256
(b) 3/16
(c) 5/52
(d) 1/8

Ans. c

Q.4. Two players, P₁ and P₂, play a game against each other. In every round of the game, each player rolls a fair die once, where the six faces of the die have six distinct numbers. Let x and y denote the readings on the die rolled by P₁ and P₂, respectively. If x > y, then P₁ scores 5 points and P₂ scores 0 point. If x =y, then each player scores 2 points. If x < y, then P₁ scores 0 point and P₂ scores 5 points. Let X_i and Y_i be the total scores of P₁ and P₂, respectively, after playing the i^th  round.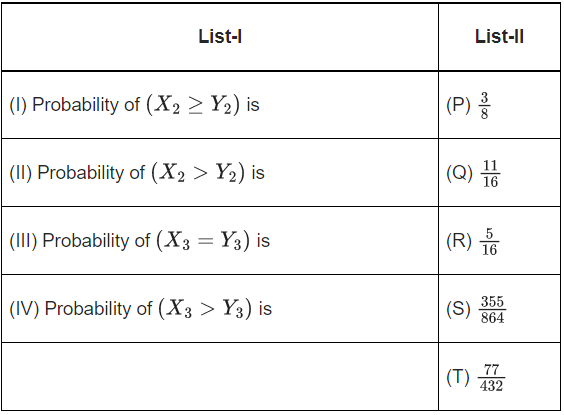

The correct option is:     (JEE Advanced 2022)
(a) (I) → (Q); (II) → (R); (III) → (T); (IV) →(S)
(b) (I) → (Q); (II) → (R); (III) → (T); (IV) → (T)
(c) (I) → (P); (II) → (R); (III) →(Q);(IV)→(S)
(d) (I) → (P); (II) → (R); (III) → (Q); (IV) → (T)

Ans. a

Q.5. In a study about a pandemic, data of 900 persons was collected. It was found that 190 persons had symptom of fever, 220 persons had symptom of cough, 220 persons had symptom of breathing problem, 330 persons had symptom of fever or cough or both, 350 persons had symptom of cough or breathing problem or both, 340 persons had symptom of fever or breathing problem or both, 30 persons had all three symptoms (fever, cough and breathing problem).
If a person is chosen randomly from these 900 persons, then the probability that the person has at most one symptom is _____.     (JEE Advanced 2022)

Ans. 0.79 and 0.81

Q.6. The sum and product of the mean and variance of a binomial distribution are 82.5 and 1350 respectively. Then the number of trials in the binomial distribution is _____.     (JEE Main 2022)

Ans. 96
Let two roots of a quadratic equation are mean = np and variance = npq.
Given np + npq = 82.5
and np(npq) = 1350
∴ Quadratic equation is
x² − 82.5x + 1350 = 0
⇒ x² − 22.5x − 60x + 1350 = 0
⇒ x − (x−22.5) − 60(x − 22.5) = 0
Mean =60 and Variance =22.5
np = 60, npq = 22.5

∴ n(5/8) = 60 ⇒ n = 96

Q.7. A bag contains 4 white and 6 black balls. Three balls are drawn at random from the bag. Let X be the number of white balls, among the drawn balls. If σ² is the variance of X, then 100σ² is equal to _____.     (JEE Main 2022)

Ans. 57
X = Number of white ball drawn



and
Variance

= 56/100
100 σ² = 56.

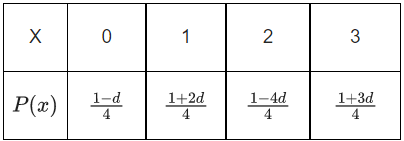
Q.8. The probability distribution of X is :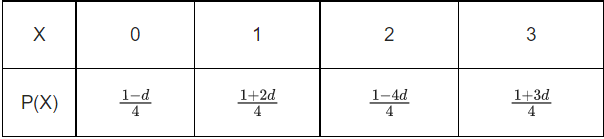

For the minimum possible value of d, sixty times the mean of X is equal to _____.     (JEE Main 2022)

Ans. 75

We know, 0 ≤ P(x) ≤ 1

⇒ 0 ≤ 1 − d ≤ 4
⇒ −1 ≤ −d ≤ 3
⇒ 1 ≥ d ≥ −3
Also,

⇒ 0 ≤ 1 + 2d ≤ 4
⇒ −1 ≤ 2d ≤ 3
⇒ −(1/2) ≤ d ≤ (3/2)
Also,

⇒ 0 ≤ 1−4d ≤ 4
⇒ −1 ≤−4d ≤ 3
⇒ 1 ≥ 4d ≥ − 3
⇒ (1/4) ≥ d ≥ − (3/4)
And,

⇒ 0 ≤ 1 + 3d ≤ 4
⇒ -1 ≤ 3d ≤ 3
⇒ -(1/3) ≤ d ≤ 1

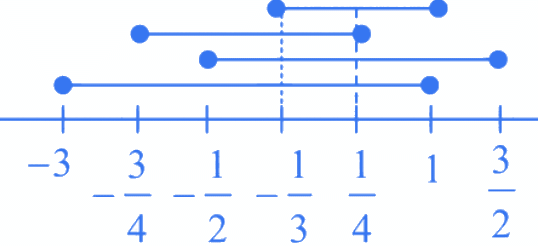
Common range is = -(1/3) to 1/4

∴ Minimum value of d = -(1/3)
We know, mean
E(x) = ∑ x. P(x)



For
∴ 60E(x) = 60 × (5/4) = 75.

Q.9. In an examination, there are 10 true-false type questions. Out of 10, a student can guess the answer of 4 questions correctly with probability (3/4) and the remaining 6 questions correctly with probability (1/4). If the probability that the student guesses the answers of exactly 8 questions correctly out of 10 is (27k/(4¹⁰)), then k is equal to ____.       (JEE Main 2022)

Ans. 479
Student guesses only two wrong. So there are three possibilities.
(i) Student guesses both wrong from 1^st section
(ii) Student guesses both wrong from 2^nd section
(iii) Student guesses two wrong one from each section
Required probabilities

Q.10. If the probability that a randomly chosen 6-digit number formed by using digits 1 and 8 only is a multiple of 21 is p, then 96 p is equal to _____.     (JEE Main 2022)

Ans. 33
Total number of numbers from given
Condition = n(s) = 2⁶.
Every required number is of the form

Here 111111 is always divisible by 21.∴ If A is divisible by 21 then
 must be divisible by 3.

For this we have 6C0 + 6C3 + 6C6 cases are there

∴ n(E) = ⁶C₀ + ⁶C₃ + ⁶C₆ = 22
∴ Required probability = 22/(2⁶) = p
∴ (11/32) = p
∴ 96p = 33

Q.11. Let S = {E₁, E₂, ........., E₈} be a sample space of a random experiment such that P(E_n) = n/36 for every n = 1, 2, ........, 8. Then the number of elements in the set {A ⊆ S : P(A) ≥ (4/5)} is  ________.     (JEE Main 2022)

Ans. 19
Here P(E_n) = (n/36) for n = 1, 2, 3, ......, 8
Here P(A)
∵ (a/36) ≥ (4/5)
∴ a ≥ 29
If one of the number from {1, 2, ......, 8} is left then total a ≥ 29 by 3 ways.
Similarly by leaving terms more 2 or 3 we get 16 more combinations.
∴ Total number of different set A possible is 16 + 3 = 19

Q.12. Let S = {1, 2, 3 ,…, 2022}. Then the probability, that a randomly chosen number n from the set S such that HCF(n, 2022) = 1, is :      (JEE Main 2022)
(a) 128/1011
(b) 166/1011
(c) 127/337
(d) 112/337

Ans. d
S = {1, 2, 3, .......... 2022}
HCF (n, 2022) = 1
⇒ n and 2022 have no common factor
Total elements = 2022
2022 = 2 × 3 × 337
M : numbers divisible by 2.
{2, 4, 6, ........, 2022} n(M) = 1011
N : numbers divisible by 3.
{3, 6, 9, ........, 2022} n(N) = 674
L : numbers divisible by 6.
{6, 12, 18, ........, 2022} n(L) = 337
n(M ∪ N) = n(M) + n(N) − n(L)
= 1011 + 674 − 337
= 1348
0 = Number divisible by 337 but not in M ∪ N
{337, 1685}
Number divisible by 2, 3 or 337
= 1348 + 2 = 1350
Required probability =(2022−1350)/2022
= (672/2022)
= 112/337

Q.13. Let A and B be two events such that P(B∣A) = (2/5), P(A∣B) = (1/7) and P(A∩B)= (1/9)⋅ Consider
(S₁) P(A′ ∪ B) = 5/6,
(S₂) P(A′ ∩ B′) = 1/18
Then      (JEE Main 2022)
(a) Both (S1) and (S2) are true
(b) Both (S1) and (S2) are false
(c) Only (S1) is true
(d) Only (S2) is true

Ans. a





S1: and

Q.14. Out of 60% female and 40% male candidates appearing in an exam, 60% candidates qualify it. The number of females qualifying the exam is twice the number of males qualifying it. A candidate is randomly chosen from the qualified candidates. The probability, that the chosen candidate is a female, is :      (JEE Main 2022)
(a) 3/4
(b) 11/16
(c) 23/32
(d) 13/16

Ans. a
P (Female) = 60/100 = 35
P (Male) = 2/5
P (Female/Qualified) = 40/60 = 2/3
P (Male/qualified)  = 20/60 = 1/3

Q.15. A six faced die is biased such that 3 × P(a prime number) = 6 × P(a composite number) = 2 × P(1). Let X be a random variable that counts the number of times one gets a perfect square on some throws of this die. If the die is thrown twice, then the mean of X is :    (JEE Main 2022)
(a) 3/11
(b) 5/11
(c) 7/11
(d) 8/11

Ans. d
Let P(a prime number) = α
P(a composite number) = β
and P(1) = γ
∵ 3α = 6β = 2γ = k (say)
and 3α+2β+γ=1
⇒ k + (k/3) + (k/2) = 1 ⇒ k = (6/11)
Mean = np where n = 2
and p = probability of getting perfect square
= P(1) + P(4) = (k/2) + (k/6) = (4/11)
So, mean =

Q.16. Let X have a binomial distribution B(n, p) such that the sum and the product of the mean and variance of X are 24 and 128 respectively. If P(X > n − 3) = (k/2ⁿ), then k is equal to :     (JEE Main 2022)
(a) 528
(b) 529
(c) 629
(d) 630

Ans. b
Mean = np =16
Variance = npq = 8
⇒ q = p = 1/2 and n = 32
P(x > n − 3) = p(x = n − 2) + p(x = n − 1) + p(x = n)
= (³²C₂ + ³²C₁ + ³²C₀).1/(2ⁿ)
= 529/(2ⁿ)

Q.17. Let S be the sample space of all five digit numbers. It p is the probability that a randomly selected number from S, is a multiple of 7 but not divisible by 5 , then 9p is equal to      (JEE Main 2022)
(a) 1.0146
(b) 1.2085
(c) 1.0285
(d) 1.1521

Ans. c
Among the 5 digit numbers,
First number divisible by 7 is 10003 and last is 99995.
⇒ Number of numbers divisible by 7.
= ((99995−10003)/7) + 1
= 12857
First number divisible by 35 is 10010 and last is 99995.
⇒ Number of numbers divisible by 35
= ((99995−10010)/35) + 1
= 2572
Hence number of number divisible by 7 but not by 5
= 12857 − 2572
= 10285
9P. = (10285/90000) × 9
= 1.0285

Q.18. Let X be a binomially distributed random variable with mean 4 and variance 4/3. Then, 54P(X ≤ 2) is equal to      (JEE Main 2022)
(a) 73/27
(b) 146/27
(c) 146/81
(d) 126/81

Ans. b
Mean = 4 = μ = np
Variance = σ² = np(1−P) = 4/3
4(1−P) = 4/3
P = 2/3
n × (2/3) = 4
n = 6
P(X = k) = ⁿC_kP^k(1 − P)^n−k
P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2)

Q.19. Let E₁, E₂, E₃ be three mutually exclusive events such that P(E₁) = (2 + 3p)/6, P(E₂) = (2 − p)/8 and P(E₃) = (1 − p)/2. If the maximum and minimum values of p are p₁ and p₂, then (p₁ + p₂) is equal to :    (JEE Main 2022)
(a) 2/3
(b) 5/3
(c) 5/4
(d) 1

Ans. b


Taking intersection of all
P ∈ [(2/3), 1)
P₁ + P₂ = 53

Q.20. The mean and variance of a binomial distribution are α and α/3 respectively. If P(X = 1) = (4/243), then P(X = 4 or 5) is equal to :     (JEE Main 2022)
(a) 5/9
(b) 64/81
(c) 16/27
(d) 145/243

Ans. c
Given, mean = np = α.
and variance = npq = α/3
⇒ q = 1/3 and p = 2/3
P(X = 1) = n.p¹.qⁿ⁻¹ = 4/243
⇒ n.(2/3).(1/3)ⁿ⁻¹ = 4/243
⇒ n = 6
P(X = 4 or 5) = ⁶C₄.(2/3)⁴.(1/3)² + ⁶C₅.(2/5)⁵.(1/3)
= 16/27

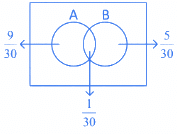
Q.21. If A and B are two events such that P(A) = 1/3, P(B) = 1/5 and P(A ∪ B) = 1/2, then P(A∣B′) + P(B∣A′) is equal to      (JEE Main 2022)
(a) 3/4
(b) 5/8
(c) 5/4
(d) 7/8

Ans. b


Now, P(A|B′) + P(B|A′) =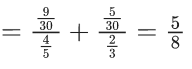
 

Q.22. If the numbers appeared on the two throws of a fair six faced die are α and β, then the probability that x² + αx + β > 0, for all 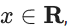is :     (JEE Main 2022)
(a) 17/36
(b) 4/9
(c) 1/2
(d) 19/36

Ans. a
For x² + αx + β >0 ∀x ∈ R to hold, we should have α² − 4β < 0
If α = 1, β can be 1, 2, 3, 4, 5, 6 i.e., 6 choices
If α = 2, β can be 2, 3, 4, 5, 6 i.e., 5 choices
If α = 3, β can be 3,4,5,6 i.e., 4 choices
If α = 4, β can be 5 or 6 i.e., 2 choices
If α = 6, No possible value for β i.e., 0 choices
Hence total favourable outcomes
= 6 + 5 + 4 + 2 + 0 + 0 = 17
Total possible choices for α and β = 6 × 6 = 36
Required probability = 17/36

Q.23. If the sum and the product of mean and variance of a binomial distribution are 24 and 128 respectively, then the probability of one or two successes is :     (JEE Main 2022)
(a) 33/(2³²)
(b) 33/(2²⁹)
(c) 33/(2²⁸)
(d) 33/(2²⁷)

Ans. c
If n is number of trails, p is probability of success and q is probability of unsuccess then, Meannand variance.
Here and Mean =np and variance =npq.  
Here
np + npq = 24 …(i)
np.npq = 128 …(ii)
and q = 1 − p …(iii)
from eq. (i), (ii) and (iii) : p = q = (1/2) and n = 32.
∴ Required probability = p(X = 1) + p(X = 2)

33/(2²⁸)

Q.24. If a random variable X follows the Binomial distribution B(5, p) such that P(X = 0) = P(X = 1), then P(X = 2)/P(X = 3) is equal to :      (JEE Main 2022)
(a) 1
(b) 10
(c) 25
(d) 5

Ans. d
Given,
n = 5
and P(X = 0) = P(X = 1)
We know, p(x = r) = ⁿC_r.p^r.q^n−r
where p + q = 1
∴ P(X = 0) = P(X = 1)
⇒⁵C₀.p⁰.q⁵ = ⁵C₁.p¹.q⁴
⇒ 1.1.(1−p)⁵ = 5.p.(1−p)⁴
⇒ 1 − p =5p
⇒ 6p = 1
⇒ p = 16
∴ q = 1−p = 1−16 = 56
Now,


= 5

Q.25. If a random variable X follows the Binomial distribution B(33, p) such that 3P(X = 0) = P(X = 1), then the value of 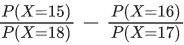 is equal to :      (JEE Main 2022)
(a) 1320
(b) 1088
(c) 120/1331
(d) 1088/1089

Ans. a
3P(X = 0) = P(X = 1)

⇒ 1 - P = 11P
⇒ P = 1/12



⇒ 11³ - 11 = 1320

Q.26. Bag A contains 2 white, 1 black and 3 red balls and bag B contains 3 black, 2 red and n white balls. One bag is chosen at random and 2 balls drawn from it at random, are found to be 1 red and 1 black. If the probability that both balls come from Bag A is 6/11, then n is equal to _____.     (JEE Main 2022)
(a) 13
(b) 6
(c) 4
(d) 3

Ans. c







⇒ n² + 9n - 52 = 0
⇒ n = 4 is only possible value

Q.27. A random variable X has the following probability distribution: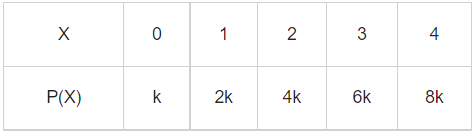

The value of P(1 < X < 4 | X ≤ 2) is equal to :       (JEE Main 2022)
(a) 4/7
(b) 2/3
(c) 3/7
(d) 4/5

Ans. a
∵ x is a random variable
∴ k + 2k + 4k + 6k + 8k = 1
∴ k = 1/21
Now, P(1 < x < 4|x ≤ 2) = 4k/7k = 4/7

Q.28. Let E₁ and E₂ be two events such that the conditional probabilities P(E₁|E₂) = 1/2, P(E₂|E₁) = 3/4 and P(E₁ ∩ E₂) = 1/8. Then :     (JEE Main 2022)
(a) P(E₁ ∩ E₂) = P(E₁).P(E₂)
(b) P(E₁′ ∩ E₂′) = P(E₁′).P(E₂)
(c) P(E₁ ∩ E₂′) = P(E₁).P(E₂)
(d) P(E₁′ ∩ E₂) = P(E₁).P(E₂)

Ans. c









⇒ P(E₁′ ∩ E₂) ≠ P(E₁).P(E₂)

Q.29. A biased die is marked with numbers 2, 4, 8, 16, 32, 32 on its faces and the probability of getting a face with mark n is 1/n. If the die is thrown thrice, then the probability, that the sum of the numbers obtained is 48, is :      (JEE Main 2022)
(a) 7/(2¹¹)
(b) 7/(2¹²)
(c) 3/(2¹⁰)
(d) 13/(2¹²)

Ans. d
There are only two ways to get sum 48, which are (32, 8, 8) and (16, 16, 16)
So, required probability


13/(2¹²)

Q.30. Let a biased coin be tossed 5 times. If the probability of getting 4 heads is equal to the probability of getting 5 heads, then the probability of getting atmost two heads is :    (JEE Main 2022)
(a) 275/6⁵
(b) 36/5⁴
(c) 181/5⁵
(d) 46/6⁴

Ans. d
Coin is tossed 5 times, so n = 5
Let, p = probability of getting heads
q = probability of getting tails.
∴ p + q = 1 ...... (1)
∴ Probability of getting 4 heads
= ⁵C₄ . p⁴ . q
And probability of getting 5 heads
= ⁵C₅ . p⁵
Given, ⁵C₄ . p⁴ . q = ⁵C₅ . p⁵
⇒ 5q = p ....... (2)
From equation (1) and (2), we get,
5q + q = 1
⇒ 6q = 1
⇒ q = 1/6
∴ p = 1 − (1/6) = (5/6)
Now, probability of getting atmost two heads
= p (x = 0) + p (x = 1) + p (x = 2)
p (x = 0) = Getting zero head in 5 trials
= ⁵C₀ . p⁰ . q⁵
p (x = 1) = Getting one head in 5 trials
= ⁵C₁ . p¹ . q⁴
p (x = 2) = Getting two heads in 5 trials
= ⁵C₂ . p² . q³
= ⁵C₀ . q⁵ + ⁵C₁ . pq⁴ + ⁵C₂ . p²q³

Q.31. Five numbers x₁, x₂, x₃, x₄, x₅ are randomly selected from the numbers 1, 2, 3, ......., 18 and are arranged in the increasing order (x₁ < x₂ < x₃ < x₄ < x₅). The probability that x₂ = 7 and x₄ = 11 is :      (JEE Main 2022)
(a) 1/136
(b) 1/72
(c) 1/68
(d) 1/34

Ans. c

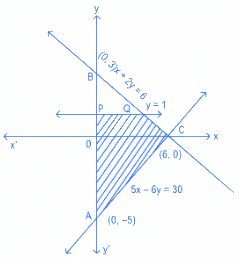
Q.32. If a point A(x, y) lies in the region bounded by the y-axis, straight lines 2y + x = 6 and 5x − 6y = 30, then the probability that y < 1 is      (JEE Main 2022)
(a) 1/6
(b) 5/6
(c) 2/3
(d) 6/7

Ans. b
The required probability



= 5/6

Q.33. The probability, that in a randomly selected 3-digit number at least two digits are odd, is      (JEE Main 2022)
(a) 19/36
(b) 15/36
(c) 13/36
(d) 23/36

Ans. a

Q.34. The probability that a randomly chosen one-one function from the set {a, b, c, d} to the set {1, 2, 3, 4, 5} satisfies f(a) + 2f(b) − f(c) = f(d) is :       (JEE Main 2022)
(a) 1/24
(b) 1/40
(c) 1/30
(d) 1/20

Ans. d
Number of one-one function from {a, b, c, d} to set {1, 2, 3, 4, 5} is ⁵P₄ = 120n(s).
The required possible set of value (f(a),  f(b), f(c), f(d)) such that f(a) + 2f(b) − f(c) = f(d) are (5,3,2,1), (5,1,2,3), (4,1,3,5), (3,1,4,5), (5,4,3,2) and (3,4,5,2)
∴ n(E) = 6
∴ Required probability = n(E)/n(S) = (6/120) = (1/20).

Q.35. The probability that a relation R from {x, y} to {x, y} is both symmetric and transitive, is equal to      (JEE Main 2022)
(a) 5/16
(b) 9/16
(c) 11/16
(d) 13/16

Ans. a

Q.36. The probability that a randomly chosen 2 × 2 matrix with all the entries from the set of first 10 primes, is singular, is equal to :     (JEE Main 2022)
(a) 133/(10⁴)
(b) 18/(10³)
(c) 19/(10³)
(d) 271/(10⁴)

Ans. c
First 10 prime numbers are
= {2, 3, 5, 7, 11, 13, 17, 19, 23, 29}
Let A is a 2 × 2 matrix,

Given that matrix A is singular.
∴ | A | = 0

⇒ ad = bc
Case I :
ad = bc condition satisfy when a = b = c = d.
For ex when a = 2, b = 2, c = 2, d = 2, then ad = bc satisfy.
Now there are 10 prime numbers.
We can choose any one of the 10 prime number in ¹⁰C₁ = 10 ways and put them in the four positions of the matrix and matrix will be singular.
∴ In this case, total favorable case = 10
Case 2 : ad = bc condition satisfies when
(1)
a = 2, d - 3 then
(a) b = 2, c = 3
(b) b = 3, c = 2
or
a = 3, d = 2 then
(a) b = 2, c = 3
(b) b = 3, c = 2
So you can see for two different prime number for a and d there are 4 possible value of b and c which satisfy ad = bc condition.
Two different values of a and d can be chosen from 10 prime numbers = ¹⁰C₂ ways
And for each combination of a and d there are 4 possible values of b and c.
∴ Total possible values = ¹⁰C₂ × 4
From case I and case II total possible values of 10 prime numbers which satisfy ad = bc condition
= 10 + ¹⁰C₂ × 4
For sample space,
Number of ways to fill element a of matrix A = chose any prime number among 10 available prime number = ¹⁰C₁ ways
Similarly,
For element b of matrix A = ¹⁰C₁ ways
For element c of matrix A = ¹⁰C₁ ways
For element d of matrix A = ¹⁰C₁ ways
∴ Sample space = ¹⁰C₁ × ¹⁰C₁ × ¹⁰C₁ × ¹⁰C₁ = 10⁴


= 190/10⁴
= 19/10³

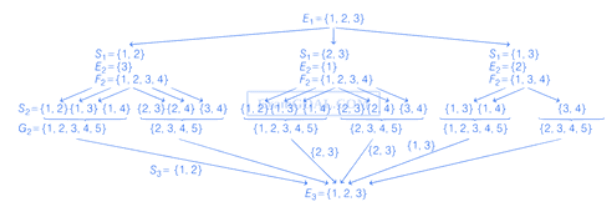
Q.37. Consider three sets E₁ = {1, 2, 3}, F₁ = {1, 3, 4} and G₁ = {2, 3, 4, 5}. Two elements are chosen at random, without replacement, from the set E₁, and let S₁ denote the set of these chosen elements. Let E₂ = E₁ − S₁ and F₂ = F₁ ∪ S₁. Now two elements are chosen at random, without replacement, from the set F₂ and let S₂ denote the set of these chosen elements.
Let G₂ = G₁ ∪ S₂. Finally, two elements are chosen at random, without replacement, from the set G₂ and let S₃ denote the set of these chosen elements.
Let E₃ = E₂ ∪ S₃. Given that E₁ = E₃, let p be the conditional probability of the event S₁ = {1, 2}. Then the value of p is      (JEE Advanced 2021)
(a) 1/5
(b) 3/5
(c) 1/2
(d) 2/5

Ans. a

To find : Probability P =
where P(A) =P(A_{1, 2}) + P(A_{1, 3}) + P(A_{2, 3})
Also, A_{1, 2} represents 1, 2 chosen at start and similarly others.
Now,

∴ Required probability

Q.38. A number of chosen at random from the set {1, 2, 3, ....., 2000}. Let p be the probability that the chosen number is a multiple of 3 or a multiple of 7. Then the value of 500p is ____.        (JEE Advanced 2021)

Ans. 214
Given, set = {1, 2, 3, ...., 2000}
Let E₁ = Event that it is a multiple of 3 = {3, 6, 9, ...., 1998}
∴ n(E₁) = 666
and E₂ = Event that it is a multiple of 7 = {7, 14, ..., 1995}
∴ n(E₂) = 285
E₁ ∩ E₂ = multiple of 21 = {21, 42, ....., 1995}
n(E₁ ∩ E₂)=95
∴ P(E₁ ∪ E₂) = P(E₁) + P(E₂) − P(E₁ ∩ E₂)

Hence,

Q.39. Three numbers are chosen at random, one after another with replacement, from the set S = {1, 2, 3, ......, 100}. Let p₁ be the probability that the maximum of chosen numbers is at least 81 and p₂ be the probability that the minimum of chosen numbers is at most 40.
The value of (125/4)p₂ is ______.        (JEE Advanced 2021)

Ans. 24.5
p₂ = 1 − p (all three numbers are > 40)

So,

Q.40. Three numbers are chosen at random, one after another with replacement, from the set S = {1, 2, 3, ......, 100}. Let p₁ be the probability that the maximum of chosen numbers is at least 81 and p₂ be the probability that the minimum of chosen numbers is at most 40.
The value of (625/4)p₁ is _____.      (JEE Advanced 2021)

Ans. 76.25
p₁ = 1 − p (all 3 numbers are ≤ 80)

So,

Q.41. Let E, F and G be three events having probabilities P(E) = (1/8), P(F) = (1/6) and P(G) = (1/4), and let P (E ∩ F ∩ G) = 110. For any event H, if H^c denotes the complement, then which of the following statements is (are) TRUE?     (JEE Advanced 2021)
(a) P(E ∩ F ∩ G^c) ≤ (1/40)
(b) P(E^c ∩ F ∩ G) ≤ (1/15)
(c) P(E ∪ F ∪ G) ≤ (13/24)
(d) P(E^c ∪ F^c ∪ G^c) ≤ (5/12)

Ans. a, b and c
For option (a)
P(E ∩ F∩ G^C) = P(E ∩ F) −P (E ∩ F ∩ G) ≤ P(E) −P(E ∩ F ∩ G)

For option (c)
P(E ∪ F ∪ G) ≤ P(E) + P(F) + P(G)

For option (d)
P(E^C ∩ F^C ∩ G^C) = 1 − P(E ∩ F ∩ G) ≥ 1 − (13/24)
P(E^C ∩ F^C ∩ G^C) ≥ (11/24) > ((5/12)

Q.42. An electric instrument consists of two units. Each unit must function independently for the instrument to operate. The probability that the first unit functions is 0.9 and that of the second unit is 0.8. The instrument is switched on and it fails to operate. If the probability that only the first unit failed and second unit is functioning is p, then 98 p is equal to ______.     (JEE Main 2021)

Ans. 28
I₁ = first unit is functioning
I₂ = second unit is functioning
P(I₁) = 0.9, P(I₂) = 0.8


98P = (8/28) x 98 = 28

Q.43. A fair coin is tossed n-times such that the probability of getting at least one head is at least 0.9. Then the minimum value of n is _______.      (JEE Main 2021)

Ans. 4
P(Head) = (1/2)
1 − P(All tail) ≥ 0.9
1−(1/2)ⁿ  ≥  0.9
⇒ (12)ⁿ ≤ 110
⇒  n_min = 4

Q.44. Let there be three independent events E₁, E₂ and E₃. The probability that only E₁ occurs is α, only E₂ occurs is β and only E₃ occurs is γ. Let 'p' denote the probability of none of events occurs that satisfies the equations (α − 2β)p = αβ and (β − 3γ)p = 2βγ. All the given probabilities are assumed to lie in the interval (0, 1).
Then, 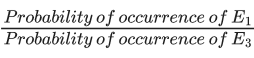 is equal to ______.       (JEE Main 2021)

Ans. 6
Let P(E₁) = x, P(E₂) = y and P(E₃) = z

⇒ α = x(1 − y) (1 − z) ......(i)
Similarly
β = (1 – x).y(1 – z) ...(ii)
γ = (1 – x)(1 – y).z ...(iii)
p = (1 – x)(1 – y)(1 – z) ...(iv)
From (i) and (iv)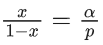
 

From (iii) and (iv)

Also given,
(α − 2β)p = αβ ⇒ αp = (α + 2p)β ....(vi)
β − 3γ)p = 2βγ ⇒ 3γp = (p - 2γ)β .....(vii)
From (vi) and (vii),

⇒ pα - 6pγ = 5γα


Now from (v) and (viii),

Q.45. Let B_i (i = 1, 2, 3) be three independent events in a sample space. The probability that only B₁ occur is α, only B₂ occurs is β and only B₃ occurs is γ. Let p be the probability that none of the events B_i occurs and these 4 probabilities satisfy the equations (α − 2β)p = αβ and (β − 3γ)p = 2βγ (All the probabilities are assumed to lie in the interval (0, 1)).
Then P(B₁)/P(B₃) is equal to ________.     (JEE Main 2021)

Ans. 6
Let x, y, z be probability of B₁, B₂, B₃ respectively

⇒ x(1 − y)(1 − z) = α
Similarly, y(1 − x)(1 − z) = β
z(1 − x)(1 − y) = γ
and (1 − x)(1 − y)(1 − z) = p
(α − 2β)p = αβ
(x(1 − y)(1 − z) −2y(1 − x)(1 − z)) (1 − x)(1 − y)(1 − z) = xy(1 − x)(1 − y)(1 − z)
x − xy − 2y + 2xy = xy
x = 2y ...... (1)
Similarly (β − 3γ)p = 2βγ
⇒ y = 3z .... (2)
From (1) & (2)
x = 6z
Now
x/z = 6

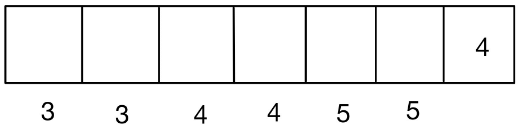
Q.46. Two squares are chosen at random on a chessboard (see figure). The probability that they have a side in common is :      (JEE Main 2021)

(a) 2/7
(b) 1/18
(c) 1/7
(d) 1/9

Ans. b
Total ways of choosing square = ⁶⁴C₂
= (64 × 63)/(2 × 1) = 32 × 63
ways of choosing two squares having common side = 2 (7 × 8) = 112
Required probability =

Q.47. Let S = {1, 2, 3, 4, 5, 6}. Then the probability that a randomly chosen onto function g from S to S satisfies g(3) = 2g(1) is :      (JEE Main 2021)
(a) 1/10
(b) 1/15
(c) 1/5
(d) 1/30

Ans. a
g(3) = 2g(1) can be defined in 3 ways
number of onto functions in this condition = 3 × 4!
Total number of onto functions = 6!
Required probability =

Q.48. Each of the persons A and B independently tosses three fair coins. The probability that both of them get the same number of heads is :      (JEE Main 2021)
(a) 1/8
(b) 5/8
(c) 5/16
(d) 1

Ans. c
Let x be the number of heads obtained by A, and y be the number of heads obtained by B.
Note that x and y are binomial variable with parameters n = 3 and p = 1/2
∴ Probability that both A and B obtained the same number of heads is
= P(x = 0). P(y = 0) + P(x = 1).P(y = 1) + P(x = 2).P(y = 2) + P(x = 3).P(y = 3)

= (1/2)⁶[ 1 + 9 + 9 + 1]
= 20/64
= 5/16

Q.49. When a certain biased die is rolled, a particular face occurs with probability (1/6)−x and its opposite face occurs with probability (1/6)+x. All other faces occur with probability 16. Note that opposite faces sum to 7 in any die. If 0 < x < (1/6), and the probability of obtaining total sum = 7, when such a die is rolled twice, is (13/96), then the value of x is :     (JEE Main 2021)
(a) 1/16
(b) 1/8
(c) 1/9
(d) 1/12

Ans. b
Probability of obtaining total sum 7 = probability of getting opposite faces.
Probability of getting opposite faces


⇒ x = (1/8)

Q.50. Two fair dice are thrown. The numbers on them are taken as λ and μ, and a system of linear equations
x + y + z = 5
x + 2y + 3z = μ
x + 3y + λz = 1
is constructed. If p is the probability that the system has a unique solution and q is the probability that the system has no solution, then:      (JEE Main 2021)
(a) p = 1/6 and q = 1/36
(b) p = 5/6 and q = 5/36
(c) p = 5/6 and q = 1/36
(d) p = 1/6 and q = 5/36

Ans. b

For no solution D = 0 ⇒ λ = 5

p = 5/6

Option (b).

Q.51. A fair die is tossed until six is obtained on it. Let x be the number of required tosses, then the conditional probability P(x ≥ 5 | x > 2) is :      (JEE Main 2021)
(a) 125/216
(b) 11/36
(c) 5/6
(d) 25/36

Ans. d


 

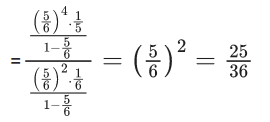
Q.52. Let A and B be independent events such that P(A) = p, P(B) = 2p. The largest value of p, for which P (exactly one of A, B occurs) = 5/9, is :      (JEE Main 2021)
(a) 1/3
(b) 2/9
(c) 4/9
(d) 5/12

Ans. d
P (Exactly one of A or B)


⇒ P(A)(1 − P(B)) + (1 − P(A))P(B) = 5/9
⇒ p(1 − 2p) + (1 − p)2p = 5/9
⇒ 36p² − 27p + 5 = 0
⇒ p = 1/3 or 5/12
p_max = 5/12

Q.53. The probability that a randomly selected 2-digit number belongs to the set {n ∈ N : (2ⁿ − 2) is a multiple of 3} is equal to       (JEE Main 2021)
(a) 1/6
(b) 2/3
(c) 1/2
(d) 1/3

Ans. c
Total number of cases = ⁹⁰C₁ = 90
Now, 2ⁿ − 2 = (3−1)ⁿ − 2
ⁿC₀3ⁿ − ⁿC₁.3ⁿ⁻¹+....+(−1)ⁿ⁻¹.ⁿC_n−13 + (−1)ⁿ.ⁿC_n − 2
= 3(3ⁿ⁻¹−n3ⁿ⁻² +...+ (−1)ⁿ⁻¹.n) + (−1)ⁿ − 2
(2ⁿ−2) is multiply of 3 only when n is odd
Required Probability = 45/90 = 1/2

Q.54. Let X be a random variable such that the probability function of a distribution is given by P(X = 0) = 1/2, P(X = j) = (1/3^j)(j = 1, 2, 3, ... , ∞). Then the mean of the distribution and P(X is positive and even) respectively are :      (JEE Main 2021)
(a) 3/8 and 1/8
(b) 3/4 and 1/8
(c) 3/4 and 1/9
(d) 3/4 and 1/16

Ans. b

P(X is even)

Q.55. A student appeared in an examination consisting of 8 true-false type questions. The student guesses the answers with equal probability. the smallest value of n, so that the probability of guessing at least 'n' correct answers is less than 1/2, is :     (JEE Main 2021)
(a) 5
(b) 6
(c) 3
(d) 4

Ans. a
P(E) < (1/2)





⇒ n − 1 ≥ 4
⇒ n ≥ 5

Q.56. Let 9 distinct balls be distributed among 4 boxes, B₁, B₂, B₃ and B₄. If the probability than B₃ contains exactly 3 balls is k(3/4)⁹ then k lies in the set :      (JEE Main 2021)
(a) {x ∈ R : |x − 3| < 1}
(b) {x ∈ R : |x − 2| ≤ 1}
(c) {x ∈ R : |x − 1| < 1}
(d) {x ∈ R : |x − 5| ≤ 1}

Ans. a
Required probability


Which satisfies |x - 3| < 1.

Q.57. Four dice are thrown simultaneously and the numbers shown on these dice are recorded in 2 × 2 matrices. The probability that such formed matrix have all different entries and are non-singular, is :      (JEE Main 2021)
(a) 45/162
(b) 21/81
(c) 22/81
(d) 43/162

Ans. d

| A | = ad − bc
Total case = 64
For non-singular matrix | A | ≠ 0 ⇒ ad − bc ≠ 0
⇒ ad ≠ bc
And a, b, c, d are all different numbers in the set {1, 2, 3, 4, 5, 6}
Now for ad = bc
(i) 6 × 1 = 2 × 3

(ii) 6 × 2 = 3 × 4

favourable cases
= ⁶C₄ × 4! - 16
required probability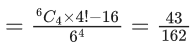
 

Q.58. Let A, B and C be three events such that the probability that exactly one of A and B occurs is (1 − k), the probability that exactly one of B and C occurs is (1 − 2k), the probability that exactly one of C and A occurs is (1 − k) and the probability of all A, B and C occur simultaneously is k², where 0 < k < 1. Then the probability that at least one of A, B and C occur is :     (JEE Main 2021)
(a) greater than 1/8 but less than 1/4
(b) greater than 1/2
(c) greater than 1/4 but less than 1/2
(d) exactly equal to 1/2

Ans. b



P(A ∩ B ∩ C) = k²
P(A) + P(B) − 2P(A ∩ B) = 1 − k .....(i)
P(B) + P(C) − 2P(B ∩ C) = 1 − k ..... (ii)
P(C) + P(A) − 2P(A ∩ C) = 1 − 2k ..... (iii)
(i) + (ii) + (iii)
P(A) + P(B) + P(C) − P(A∩B) − P(B∩C) − P(C∩A) = −4k + 32
So,



P(A ∪ B ∪ C) > (1/2)

Q.59. The probability of selecting integers a∈[− 5, 30] such that x² + 2(a + 4)x − 5a + 64 > 0, for all x ∈ R, is :      (JEE Main 2021)
(a) 7/36
(b) 2/9
(c) 1/6
(d) 1/4

Ans. b
D < 0
⇒ 4(a + 4)² − 4(−5a + 64) < 0
⇒ a² + 16 + 8a + 5a − 64 < 0
⇒ a² + 13a − 48 < 0
⇒ (a + 16) (a − 3) < 0
⇒ a ∈ (−16, 3)
∴ Possible a : {−5, −4, ............., 3}
∴ Required probability = 8/36 = 2/9

Q.60. Words with or without meaning are to be formed using all the letters of the word EXAMINATION. The probability that the letter M appears at the fourth position in any such word is :      (JEE Main 2021)
(a) 1/66
(b) 1/11
(c) 1/9
(d) 2/11

Ans. b
AAEIIMNNOTX
----------------M----------------
Total words with M at fourth Place = 10!/(2!2!2!)
Total words = 11!/(2!2!2!)
Required probability = 10!/11! = (1/11)

Q.61. Let in a Binomial distribution, consisting of 5 independent trials, probabilities of exactly 1 and 2 successes be 0.4096 and 0.2048 respectively. Then the probability of getting exactly 3 successes is equal to :     (JEE Main 2021)
(a) 40/243
(b) 128/625
(c) 80/243
(d) 32/625

Ans. d
⁵C₁p¹q⁴ = 0.4096 ..... (1)
⁵C₂p²q³ = 0.2048 ..... (2)
(1)/(2) ⇒ (q/2p) = 2 ⇒ q = 4p
p + q = 1 ⇒ P = 1/5, q = 4/5
P (exactly 3) =

Q.62. Let a computer program generate only the digits 0 and 1 to form a string of binary numbers with probability of occurrence of 0 at even places be 1/2 and probability of occurrence of 0 at the odd place be 1/3. Then the probability that '10' is followed by '01' is equal to :     (JEE Main 2021)
(a) 1/18
(b) 1/3
(c) 1/9
(d) 1/6

Ans. c
P(0 at even place) = 1/2
P(0 at odd place) = 1/3
P(1 at even place) = 1/2
P(1 at odd place) = 2/3
P(10 is followed by 01)

 = 1/9

Q.63. Two dies are rolled. If both dices have six faces numbered 1, 2, 3, 5, 7 and 11, then the probability that the sum of the numbers on the top faces is less than or equal to 8 is :    (JEE Main 2021)
(a) 4/9
(b) 1/2
(c) 5/12
(d) 17/36

Ans. d
n(S) = 36
possible ordered pair :
(1, 1), (1, 2), (1, 3), (1, 5), (1, 7),
(2, 1), (2, 2), (2, 3), (2, 5),
(3, 1), (3, 2), (3, 3), (3, 5),
(5, 1), (5, 2), (5, 3),
(7, 1)
Number of favourable outcomes = 17
Probability = 17/36.

Q.64. Let A denote the event that a 6-digit integer formed by 0, 1, 2, 3, 4, 5, 6 without repetitions, be divisible by 3. Then probability of event A is equal to :      (JEE Main 2021)
(a) 4/9
(b) 9/56
(c) 11/27
(d) 3/7

Ans. a
Total cases :

n(s) = 6 . 6!
Favourable cases :
Number divisible by 3 ≡ Sum of digits must be divisible by 3
Case - I
1, 2, 3, 4, 5, 6
Number of ways = 6!
Case - II
0, 1, 2, 4, 5, 6
Number of ways = 5 . 5!
Case - III
0, 1, 2, 3, 4, 5
Number of ways = 5 . 5!
n(favourable) = 6! + 2 . 5 . 5!

Q.65. A pack of cards has one card missing. Two cards are drawn randomly and are found to be spades. The probability that the missing card is not a spade, is :      (JEE Main 2021)
(a) 39/50
(b) 3/4
(c) 22/425
(d) 52/867

Ans. a
Consider the events,
E₁ = missing card is spade
E₂ = missing card is not a spade
A = Two spade cards are drawn

= 39/50

Q.66. A seven digit number is formed using digits 3, 3, 4, 4, 4, 5, 5. The probability, that number so formed is divisible by 2, is :      (JEE Main 2021)
(a) 1/7
(b) 4/7
(c) 6/7
(d) 3/7

Ans. d
Digits = 3, 3, 4, 4, 4, 5, 5
Total 7 digit numbers = (7!/2!2!3!)
Number of 7 digit number divisible by 2 ⇒ last digit = 4

Now 7 digit numbers which are divisible by 2 = (6!/2!2!2!)
Required probability =

Q.66. A fair coin is tossed a fixed number of times. If the probability of getting 7 heads is equal to probability of getting 9 heads, then the probability of getting 2 heads is :     (JEE Main 2021)
(a) 15/2⁸
(b) 15/2¹²
(c) 15/2¹³
(d) 15/2¹⁴

Ans. c
Let the coin be tossed n-times
P(H) = P(T) = 1/2


P(7 heads) = P(9 heads)
ⁿC₇ = nC9 ⇒ n = 16
P(2 heads) =  
P(2 heads) = 15/(2¹³)

Q.68. In a group of 400 people, 160 are smokers and non-vegetarian; 100 are smokers and vegetarian and the remaining 140 are non-smokers and vegetarian. Their chances of getting a particular chest disorder are 35%, 20% and 10% respectively. A person is chosen from the group at random and is found to be suffering from the chest disorder. The probability that the selected person is a smoker and non-vegetarian is :     (JEE Main 2021)
(a) 14/45
(b) 8/45
(c) 7/45
(d) 28/45

Ans. d
Consider following events
A : Person chosen is a smoker and non vegetarian.
B : Person chosen in a smoker and vegetarian.
C : Person chosen is a non-smoker and vegetarian.
E : Person chosen has a chest disorder
Given
P(A) = 160/400
P(B) = 100/400
P(C) = 140/400
P(EA) = 35/100
P(EB) = 20/100
P(EC) = 10/100
To find


= 28/45

Q.69. Let A be a set of all 4-digit natural numbers whose exactly one digit is 7. Then the probability that a randomly chosen element of A leaves remainder 2 when divided by 5 is :      (JEE Main 2021)
(a) 2/9
(b) 1/5
(c) 122/297
(d) 97/297

Ans. d
n(s) = n(when 7 appears on thousands place)
+ n (7 does not appear on thousands place)
= 9 × 9 × 9 + 8 × 9 × 9 × 3
= 33 × 9 × 9
n(E) = n(last digit 7 & 7 appears once)
+n(last digit 2 when 7 appears once)
= 8 × 9 × 9 + (3 × 9 × 9 - 2 × 9)

Q.70. The coefficients a, b and c of the quadratic equation, ax² + bx + c = 0 are obtained by throwing a dice three times. The probability that this equation has equal roots is :      (JEE Main 2021)
(a) 1/72
(b) 5/216
(c) 1/36
(d) 1/54

Ans. b
ax² + bx + c = 0
a, b, c ∈ {1,2,3,4,5,6}
n(s) = 6 × 6 × 6 = 216
For equal roots, D = 0 ⇒ b² = 4ac
⇒ ac = b²/4
Favourable case :
If b = 2, ac = 1 ⇒ a = 1, c = 1
If b = 4, ac = 4 :
a = 1, c = 4
a = 4, c = 1
a = 2, c = 2
If b = 6, ac = 9 ⇒ a = 3, c = 3
∴ Favorable cases = 5
∴ Required probability = 5/216.

Q.71. When a missile is fired from a ship, the probability that it is intercepted is 1/3 and the probability that the missile hits the target, given that it is not intercepted, is 3/4. If three missiles are fired independently from the ship, then the probability that all three hit the target, is :     (JEE Main 2021)
(a) 3/4
(b) 3/8
(c) 1/27
(d) 1/8

Ans. d
Probability of not getting intercepted = 2/3
When it is not intercepted, probability of missile hitting target = 3/4
∴ So when such 3 missiles launched then P (all 3 hitting the target)

= 1/8

Q.72. The probability that two randomly selected subsets of the set {1, 2, 3, 4, 5} have exactly two elements in their intersection, is :     (JEE Main 2021)
(a) 135/2⁹
(b) 65/2⁸
(c) 65/2⁷
(d) 35/2⁷

Ans. a
Given, set P = {1, 2, 3, 4, 5}
Let the two subsets be A and B
Then, n (A ∩ B) = 2 (as given in question)
We can choose two elements from set P in ⁵C₂ ways.
After choosing two common elements for set A and B, each of remaining three elements from set P have three choice (1) It can go to set A (2) It can go to set B (3) It don't go to any sets it stays at set P.
∴ Total ways for the three elements = 3 × 3 × 3 = 3³
∴ Required probability

Q.73. An ordinary dice is rolled for a certain number of times. If the probability of getting an odd number 2 times is equal to the probability of getting an even number 3 times, then the probability of getting an odd number for odd number of times is :     (JEE Main 2021)
(a) 5/36
(b) 3/16
(c) 1/2
(d) 1/32

Ans. c
P(odd no. twice) = P(even no. thrice)

Success is getting an odd number then P(odd successes) = P(1) + P(3) + P(5)

= 16/2⁵ = 1/2