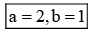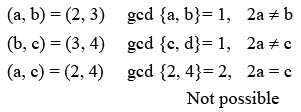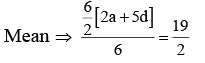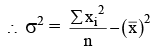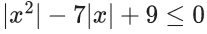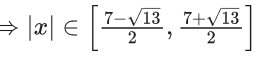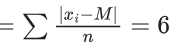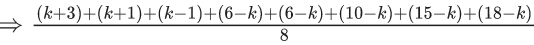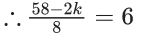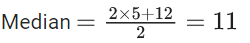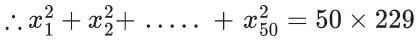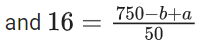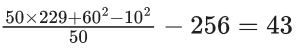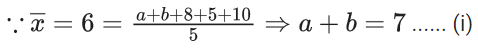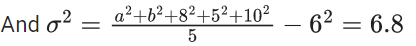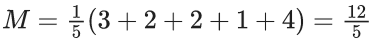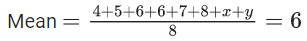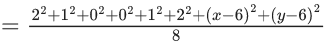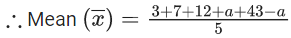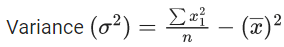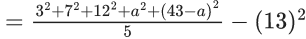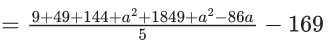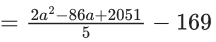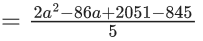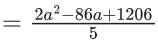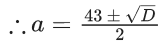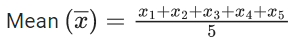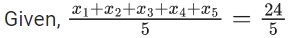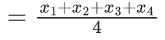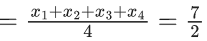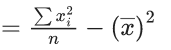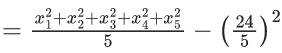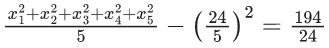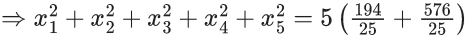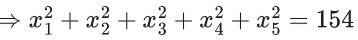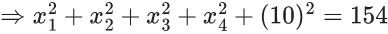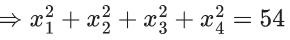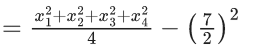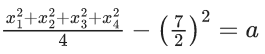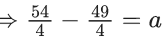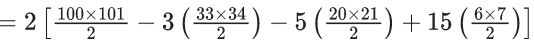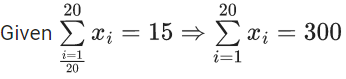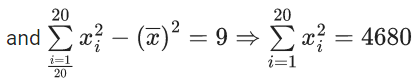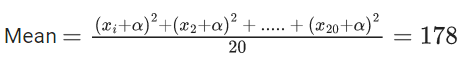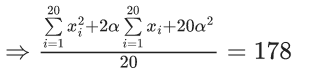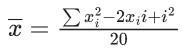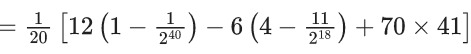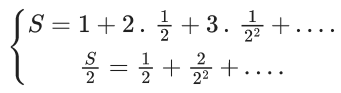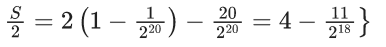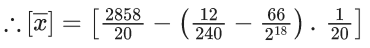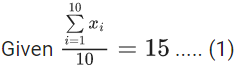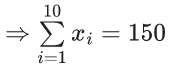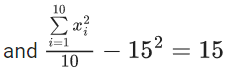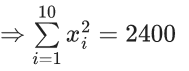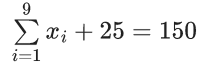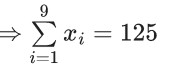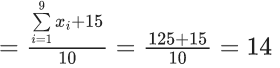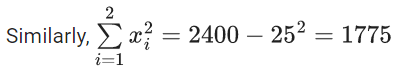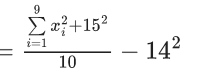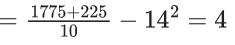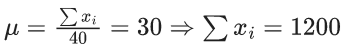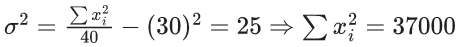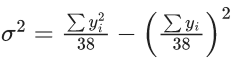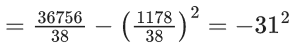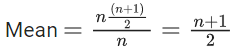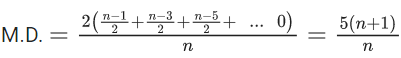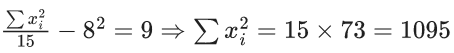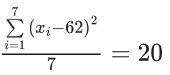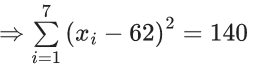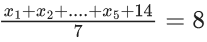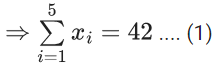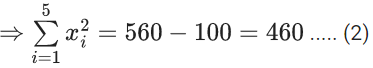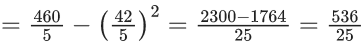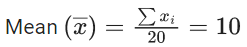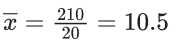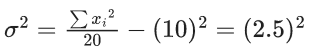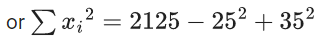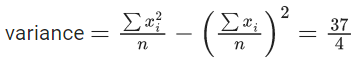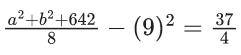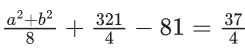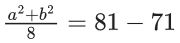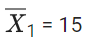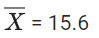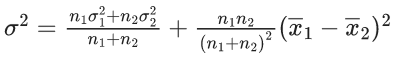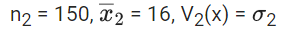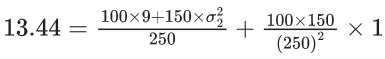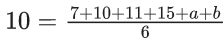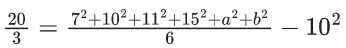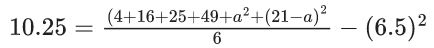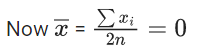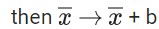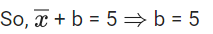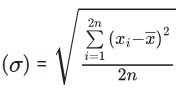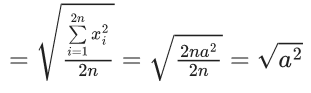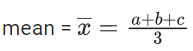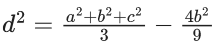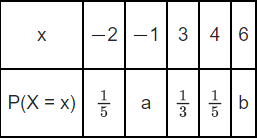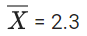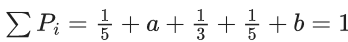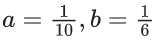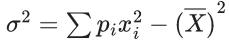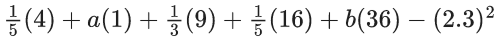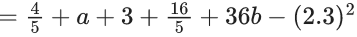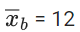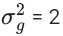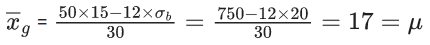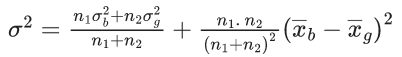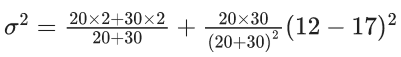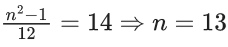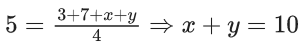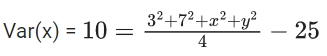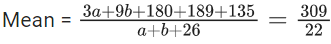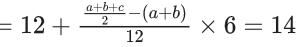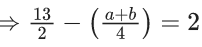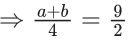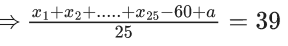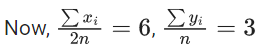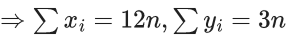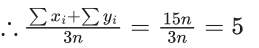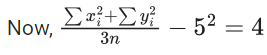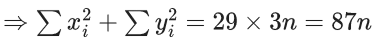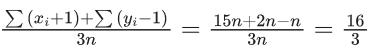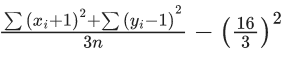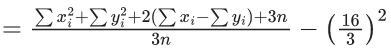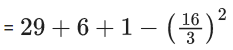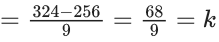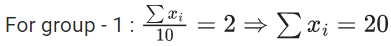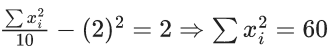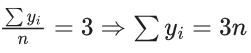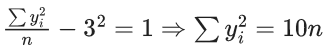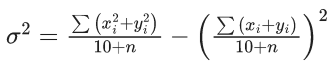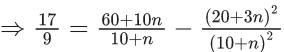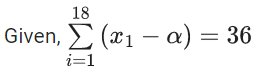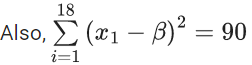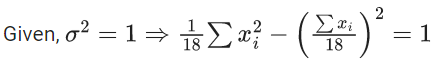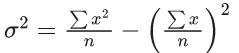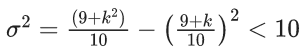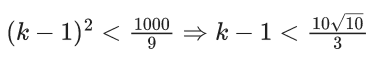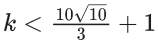JEE Main Previous Year Questions (2021-23): Miscellaneous (Sets, Relations and Statistics) PDF Download

Q.1. The relation R = {(a, b): gcd⁡(a, b) = 1,2a ≠ b, a, b∈Z} is :        (JEE Main 2023)
(a) reflexive but not symmetric
(b) transitive but not reflexive
(c) symmetric but not transitive
(d) neither symmetric nor transitive

Ans. d
gcd (a, b) = 1, 2a ≠ b
reflexive gcd (a, a) = a Not possible
symmetric gcd (b, a) = 1 & 2a ≠ b Not possible

transitive

Q.2. The minimum number of elements that must be added to the relation R = {(a, b), (b, c), (b, d)} on the set {a, b, c, d} so that it is an equivalence relation, is        (JEE Main 2023)

Ans. 13
1, 2, 3, 4 → for reflexive
5, 6, 7 → for symmetric
8, 9, 10, 11, 12, 13 → for transitive

Q.3. Let the six numbers a₁, a₂ , a₃ , a₄, a₅ , a₆, be in A.P. and a₁ + a₃ = 10. If the mean of these six numbers is 19/2 and their variance is σ², then 8σ² is equal to :        (JEE Main 2023)
(a) 210
(b) 220
(c) 200
(d) 105

Ans.  a
a + (a + 2d) = 10 ⇒ a + d = 5 ...(1)

2a + 5d = 19 ...(2)
from (1) and (2)
3d = 9 ⇒ d = 3; a = 2


8σ² = 932 - 722 = 210

Q.4. Let R be a relation from the set {1, 2, 3,…,60} to itself such that R = {(a, b) : b = pq, where p, q ⩾ 3 are prime numbers}. Then, the number of elements in R is:      (JEE Main 2022)
(a) 600
(b) 660
(c) 540
(d) 720

Ans. b
b can take its values as 9, 15, 21, 33, 39, 51, 57, 25, 35, 55, 49
b can take these 11 values and a can take any of 60 values
So, number of elements in R = 60 × 11 = 660

Q.5. Let 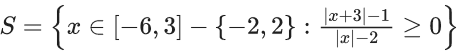 and T = { 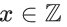: x² − 7|x| + 9 ≤ 0}. Then the number of elements in S ∩ T is :      (JEE Main 2022)
(a) 7
(b) 5
(c) 4
(d) 3

Ans. d


As x∈Z
So, x can be ±2, ±3, ±4, ±5
Out of these values of x,
x = 3, −4, −5
satisfy S as well
n(S ∩ T) = 3

Q.6. For 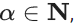, consider a relation  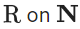given by  is a multiple of 7}. The relation 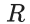 is an equivalence relation if and only if :     (JEE Main 2022)
(a) α = 14
(b) α is a multiple of 4
(c) 4 is the remainder when α is divided by 10
(d) 4 is the remainder when α is divided by 7

Ans. d
R = {(x, y): 3x + αy is multiple of 7}, now R to be an equivalence relation
(1) R should be reflexive : (a, a) ∈ R ∀ a ∈ N
∴ 3a + aα = 7k
∴ (3 +α)a = 7k
∴ 3 + α = 7k₁ ⇒ α = 7k₁ − 3
= 7k₁ + 4
(2) R should be symmetric : aRb⇔bRa
aRb : 3a + (7k − 3)b = 7m
⇒ 3(a−b) + 7kb = 7m
⇒ 3(b−a) + 7ka = 7m
So, aRb ⇒ bRa
∴ R will be symmetric for a = 7k₁ − 3
(3) Transitive : Let (a, b) ∈ R, (b, c) ∈ R
⇒ 3a + (7k − 3)b = 7k₁ and
3b + (7k₂ − 3)c = 7k₃
Adding 3a + 7kb + (7k₂ − 3)c = 7(k₁ + k₃)
3a + (7k2 − 3)c = 7m
∴ (a, c) ∈ R
∴ R is transitive
∴ α = 7k − 3 = 7k + 4 

Q.7. Let R₁ and R₂ be two relations defined on R by
aR₁b ⇔ ab ≥ 0 and aR₂b ⇔ a ≥ b
Then,        (JEE Main 2022)
(a) R₁ is an equivalence relation but not R₂
(b) R₂ is an equivalence relation but not R₁
(c) both R₁ and R₂ are equivalence relations
(d) neither R₁ nor R₂ is an equivalence relation

Ans. d
aR₁b ⇔ ab ≥ 0
So, definitely (a, a) ∈ R₁ as a₂ ≥ 0
If (a, b) ∈ R₁ ⇒ (b, a) ∈ R₁
But if (a, b) ∈ R₁,(b, c) ∈ R₁
⇒ Then (a, c) may or may not belong to R₁
{Consider a = −5, b = 0, c = 5 so (a, b) and (b, c) ∈ R₁ but ac < 0}
So, R₁ is not equivalence relation
aR₂b ⇔ a ≥ b
(a, a) ∈ R₂ ⇒ so reflexive relation
If (a, b) ∈ R₂ then (b, a) may or may not belong to R₂
⇒ So not symmetric
Hence it is not equivalence relation

Q.8. Let A = {x ∈ R:|x + 1| < 2} and B = {x ∈ R:|x − 1| ≥ 2}. Then which one of the following statements is NOT true?      (JEE Main 2022)
(a) A − B = (−1, 1)
(b) B − A = R−(−3, 1)
(c) A ∩ B = (−3, −1]
(d) A ∪ B = R−[1, 3)

Ans. b
A = (−3, 1) and B = (− ∞, −1] ∪ [3, ∞)
So, A − B = (−1, 1)
B − A = (− ∞, −3] ∪ [3, ∞) = R − (−3, 3)
A ∩ B = (−3, −1]
and A ∪ B = (− ∞, 1) ∪ [3, ∞) = R − [1, 3)

Q.9. Let R₁ = {(a, b) ∈ N × N : |a − b| ≤ 13} and
R₂ = {(a, b) ∈ N × N : |a − b| ≠ 13}. Then on N :       (JEE Main 2022)
(a) Both R₁ and R₂ are equivalence relations
(b) Neither R₁ nor R₂ is an equivalence relation
(c) R₁ is an equivalence relation but R₂ is not
(d) R₂ is an equivalence relation but R₁ is not

Ans. b
R₁ = {(a, b) ∈ N × N:|a−b| ≤ 13} and
R₂ = {(a, b) ∈ N × N : |a−b| ≠ 13}
In R₁: ∵|2−11| = 9 ≤ 13
∴ (2, 11) ∈ R₁ and (11, 19) ∈ R₁ but (2, 19) ∉ R₁
∴ R₁ is not transitive
Hence R₁ is not equivalence
In R₂ : (13, 3) ∈ R₂ and (3, 26) ∈ R₂ but (13, 26) ∉ R₂ (∵ |13 − 26| = 13)
∴ R₂ is not transitive
Hence R₂ is not equivalence.

Q.10. Let a set A = A₁ ∪ A₂ ∪ ..... ∪ A_k, where A_i ∩ A_j = ϕ for i  ≠  j, 1 ≤ j, j ≤  k. Define the relation R from A to A by R = {(x, y) : y ∈ A_i if and only if x ∈ A_i, 1 ≤ i ≤ k}. Then, R is :        (JEE Main 2022)
(a) reflexive, symmetric but not transitive.
(b) reflexive, transitive but not symmetric.
(c) reflexive but not symmetric and transitive.
(d) an equivalence relation.

Ans. d
R = {(x, y) : y ∈ A_i, iff x ∈ A_i 1 ≤ i ≥ k}
(1) Reflexive
(a, a) ⇒ a ∈ Ai iff a ∈ A_i
(2) Symmetric
(a, b) ⇒ a ∈ Ai iff b ∈ A_i
(b, a) ∈ R as b ∈ A_i iff a ∈ A_i
(3) Transitive
(a, b) ∈ R & (b, c) ∈ R.
⇒ a ∈ A_i iff b ∈ A_i & b ∈ A_i iff c ∈ A_i
⇒ a ∈ A_i iff c ∈ A_i
⇒ (a, c) ∈ R.
⇒ RElation is equivalnece.

Q.11. If the mean deviation about median for the numbers 3, 5, 7, 2k, 12, 16, 21, 24, arranged in the ascending order, is 6 then the median is      (JEE Main 2022)
(a) 11.5
(b) 10.5
(c) 12
(d) 11

Ans. d

Mean deviation


k = 5

Q.12. The mean and standard deviation of 50 observations are 15 and 2 respectively. It was found that one incorrect observation was taken such that the sum of correct and incorrect observations is 70. If the correct mean is 16, then the correct variance is equal to :      (JEE Main 2022)
(a) 10
(b) 36
(c) 43
(d) 60

Ans. c
Given σ = 2 ⇒ σ² = 4
∴ x₂ + x₂ +.....+ x₅₀ = 15 × 50 = 750


Let a be the correct observation and b is the incorrect observation then  a + b = 70

∴ a − b = 50 ⇒ a = 60, b = 10
∴ Correct variance =

Q.13. The mean of the numbers a, b, 8, 5, 10 is 6 and their variance is 6.8. If M is the mean deviation of the numbers about the mean, then 25 M is equal to :      (JEE Main 2022)
(a) 60
(b) 55
(c) 50
(d) 45

Ans. a


⇒ a² + b² = 25 ..... (ii)
From (i) and (ii) (a, b) = (3, 4) or (4, 3)
Now mean deviation about mean

⇒ 25M = 60

Q.14. Let X be a random variable having binomial distribution B(7, p). If P(X = 3) = 5P(x = 4), then the sum of the mean and the variance of X is :      (JEE Main 2022)
(a) 105/16
(b) 7/16
(c) 77/36
(d) 49/16

Ans. c
Given P(X = 3) = 5P(X = 4) and n = 7
⇒ ⁷C₃p³q⁴ = 5. ⇒ ⁷C₄p⁴q³
⇒ q = 5p and also p + q = 1
⇒ p =1/6 and q = 5/6
Mean = 7/6 and variance = 35/36
Mean + Variance = (7/6) + (35/36) = 77/36

Q.15. The mean and variance of the data 4, 5, 6, 6, 7, 8, x, y, where x < y, are 6 and 9/4 respectively. Then x⁴ + y² is equal to     (JEE Main 2022)
(a) 162
(b) 320
(c) 674
(d) 420

Ans. b

∴ x + y = 12 ..... (i)
And variance

= (9/4)
∴ (x−6)²+(y−6)²=8 ..... (ii)
From (i) and (ii)
x = 4 and y = 8
∴ x⁴ + y² = 320

Q.16. The number of values of a ∈ N such that the variance of 3, 7, 12, a, 43 − a is a natural number is :       (JEE Main 2022)
(a) 0
(b) 2
(c) 5
(d) infinite

Ans. a
Given,
5 numbers are 3, 7, 12, a, 43 − a

= 65/5 = 13
We know,






= (2/5)(a² - 43a + 603)
Variance will be natural number if a² − 43a + 603 in multiple of 5.
∴ a² − 43a + 603 = 5n
⇒ a² − 43a + 603 − 5n = 0 ..... (1)

Now "a" will be natural number if
(1) D is a perfect square and
(2) 43 ± √D is multiple of 2
From equation (1),
D = (−43)² − 4.1.(603 − 5n)
= 1849 − 2412 + 20n
= 20n − 563
For any value of n, unit digit of 20n is always 0. Then 20n − 563 will give a number whose unit digit is 7.
For perfect square numbers ex : 1² = 1, 2² = 4, 3² = 9, 4² = 16, 5² = 25, 6² = 36, 7² = 49, 8² = 64, 9² = 81, 10² = 100
So, unit digit is either 1, 4, 6, 5, 6, 9, 0 it can't be 7. So D can't be perfect square.

Q.17. Let the mean and the variance of 5 observations x₁, x₂, x₃, x_4, x₅ be 24/5 and 194/25 respectively. If the mean and variance of the first 4 observation are 7/2 and a respectively, then (4a + x₅) is equal to:     (JEE Main 2022)
(a) 13
(b) 15
(c) 17
(d) 18

Ans. b


⇒ x₁ + x₂ + x₃ + x₄ + x₅ = 24 ...... (1)
Now, Mean of first 4 observation

Given,
⇒ x₁ + x₂ + x₃ + x₄ = 14 ...... (2)
From equation (1) and (2), we get
14 + x₅ = 24
⇒ x₅ = 10
Now, variance of first 5 observation


Given,





Now, variance of first 4 observation

Given,


⇒ a = (5/4)
∴ 4a + x₅
= 4 x (5/4) + 10 = 15

Q.18. Let S = {4, 6, 9} and T = {9, 10, 11 ,…, 1000}. If A = {a₁ + a₂ +…+ a_k : k ∈ N, a₁, a₂, a₃ ,…, a_k ϵ S}, then the sum of all the elements in the set T−A is equal to _______.     (JEE Main 2022)

Ans. 11
Here S = {4, 6, 9}
And T = {9, 10, 11, ...... ,1000}.
We have to find all numbers in the form of 4x + 6y + 9z, where x, y, z ∈ {0, 1, 2,......}.
If a and b are coprime number then the least number from which all the number more than or equal to it can be express as ax + by where x, y ∈ {0, 1, 2, ......} is (a − 1).(b − 1).
Then for 6y + 9z = 3(2y + 3z)
All the number from (2 − 1).(3 − 1) = 2 and above can be express as 2x + 3z (say t).
Now 4x + 6y + 9z = 4x + 3 (t + 2)
= 4x + 3t + 6
again by same rule 4x + 3t, all the number from (4 − 1)(3 − 1) = 6 and above can be express from 4x + 3t.
Then 4x + 6y + 9z express all the numbers from 12 and above.
again 9 and 10 can be express in form 4x + 6y + 9z.
Then set A = {9, 10, 12, 13 ,...., 1000}.
Then T − A = {11}
Only one element 11 is there.
Sum of elements of T - A = 11

Q.19. Let A = {1, 2, 3, 4, 5, 6, 7} and B = {3, 6, 7, 9}. Then the number of elements in the set {C ⊆ A : C ∩ B ≠ ϕ} is ______.     (JEE Main 2022)

Ans. 112
As C ∩ B ≠ ϕ, c must be not be formed by {1, 2, 4, 5}
∴ Number of subsets of A = 2⁷ = 128
and number of subsets formed by {1, 2, 4, 5} = 16
∴ Required no. of subsets = 2⁷ − 2⁴ = 128 − 16 = 112

Q.20. Let A = {1, 2, 3, 4, 5, 6, 7}. Define B = {T ⊆ A : either 1 ∉ T or 2 ∈ T} and C = {T ⊆ A : T the sum of all the elements of T is a prime number }. Then the number of elements in the set B ∪ C is ______.        (JEE Main 2022)

Ans. 107
∵ (B ∪ C)′ = B′ ∩ C′
B' is a set containing sub sets of A containing element 1 and not containing 2.
And C' is a set containing subsets of A whose sum of elements is not prime.
So, we need to calculate number of subsets of {3, 4, 5, 6, 7} whose sum of elements plus 1 is composite.
Number of such 5 elements subset = 1
Number of such 4 elements subset = 3 (except selecting 3 or 7)
Number of such 3 elements subset = 6 (except selecting {3, 4, 5}, {3, 6, 7}, {4, 5, 7} or {5, 6, 7})
Number of such 2 elements subset = 7 (except selecting {3, 7}, {4, 6}, {5, 7})
Number of such 1 elements subset = 3 (except selecting {4} or {6})
Number of such 0 elements subset = 1
n(B′ ∩ C′) = 21 ⇒ n(B ∪ C) = 2⁷ − 21 = 107

Q.21. The sum of all the elements of the set {α ∈ {1, 2 ,....., 100} : HCF(α, 24) = 1} is __________.     (JEE Main 2022)

Ans. 1633
The numbers upto 24 which gives g.c.d. with 24 equals to 1 are 1, 5, 7, 11, 13, 17, 19 and 23.
Sum of these numbers = 96
There are four such blocks and a number 97 is there upto 100.
∴ Complete sum
= 96 + (24 × 8 + 96) + (48 × 8 + 96) + (72 × 8 + 96) + 97
= 1633

Q.22. Let A = {n ∈ N : H.C.F. (n, 45) = 1} and Let B = {2k : k ∈ {1, 2, ......., 100}}. Then the sum of all the elements of A ∩ B is _______.       (JEE Main 2022)

Ans. 5264
Sum of all elements of A ∩ B = 2 [Sum of natural numbers upto 100 which are neither divisible by 3 nor by 5]

= 10100 - 3366 - 2100 + 630
= 5264

Q.23. Let A = {1, a₁, a₂ ....... a₁₈, 77} be a set of integers with 1 < a₁ < a₂ < ....... < a₁₈ < 77. Let the set A + A = {x + y : x, y ∈ A} contain exactly 39 elements. Then, the value of a₁ + a₂ + ...... + a₁₈ is equal to _____.      (JEE Main 2022)

Ans. 702

Q.24. Let R₁ and R₂ be relations on the set {1, 2, ......., 50} such that
R₁ = {(p, pⁿ) : p is a prime and n ≥ 0 is an integer} and
R₂ = {(p, pⁿ) : p is a prime and n = 0 or 1}.
Then, the number of elements in R₁ − R₂ is ______.      (JEE Main 2022)

Ans. 8
R₁−R₂ = {(2, 2²), (2, 2³), (2, 2⁴), (2, 2⁵), (3, 3²), (3, 3³), (5, 5²), (7, 7²)}
So number of elements = 8

Q.25. Let S = {1, 2, 3, 4}. Then the number of elements in the set { f : S × S → S : f is onto and f (a, b) = f (b, a) ≥ a ∀ (a, b) ∈ S × S } is ________.       (JEE Main 2022)

Ans. 37
There are 16 ordered pairs in S×S. We write all these ordered pairs in 4 sets as follows.
A = {(1, 1)}
B = {(1, 4), (2, 4),(3, 4)(4, 4),(4, 3),(4, 2),(4, 1)}
C = {(1, 3),(2, 3),(3, 3),(3, 2),(3, 1)}
D = {(1, 2),(2, 2),(2, 1)}
All elements of set B have image 4 and only element of A has image 1.
All elements of set C have image 3 or 4 and all elements of set D have image 2 or 3 or 4 .
We will solve this question in two cases.
Case I: When no element of set C has image 3.
Number of onto functions =2 (when elements of set D have images 2 or 3)
Case II: When atleast one element of set C has image 3.
Number of onto functions = (2³−1)(1+2+2) =35
Total number of functions = 37.

Q.26. Let the mean and the variance of 20 observations x₁, x₂ ,…, x₂₀ be 15 and 9 , respectively. For 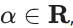, if the mean of (x₁ + α)², (x₂ + α)² ,…, (x₂₀ + α)² is 178 , then the square of the maximum value of α is equal to _____.       (JEE Main 2022)

Ans. 4




⇒ 4680 + 600α + 20α² = 3560
⇒ α² + 30α + 56 = 0
⇒ α² + 28α + 2α + 56 = 0
⇒ (α+28)(α+2) = 0
α_max = −2 ⇒ α_max² = 4.

Q.27. Let x₁, x₂, x₃ ,…, x₂₀ be in geometric progression with x₁ = 3 and the common ratio 1/2. A new data is constructed replacing each x_i by (x_i − i)². If  the mean of new data, then the greatest integer less than or equal to  ______.       (JEE Main 2022)

Ans. 142
x₁, x₂, x₃ ,....., x₂₀ are in G.P.
x₁ = 3, r = (1/2)





= 142

Q.28. The mean and variance of 10 observations were calculated as 15 and 15 respectively by a student who took by mistake 25 instead of 15 for one observation. Then, the correct standard deviation is _____.     (JEE Main 2022)

Ans. 2




Replacing 25 by 15 we get


∴ Correct mean

∴ Correct variance

∴ Correct S.D = √4 = 2.

Q.29. The mean and standard deviation of 40 observations are 30 and 5 respectively. It was noticed that two of these observations 12 and 10 were wrongly recorded. If σ is the standard deviation of the data after omitting the two wrong observations from the data, then 38σ² is equal to _____.     (JEE Main 2022)

Ans. 238


After omitting two wrong observations
∑y_i = 1200 − 12 − 10 = 1178
∑y_i² = 37000 − 144 − 100 = 36756
Now

= 36σ² = 36756 - 36518 = 238

Q.30. If the mean deviation about the mean of the numbers 1, 2, 3, ____, n, where n is odd, is 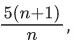 then n is equal to _____.       (JEE Main 2022)

Ans. 21


⇒ ((n−1) + (n−3) + (n−5)+ ... 0) = 5(n+1)
⇒ (n+1)/4)).(n−1) = 5(n+1)
So, n = 21

Q.31. The mean and standard deviation of 15 observations are found to be 8 and 3 respectively. On rechecking it was found that, in the observations, 20 was misread as 5. Then, the correct variance is equal to ______.       (JEE Main 2022)

Ans. 17

Let be corrected mean  = 9
∑x²_c = 1095 - 25 + 400 = 1470
Correct variance = (1470/15) - (9)² = 98 - 81 = 17

Q.32. Suppose a class has 7 students. The average marks of these students in the mathematics examination is 62, and their variance is 20. A student fails in the examination if he/she gets less than 50 marks, then in worst case, the number of students can fail is ______.     (JEE Main 2022)

Ans. 0
According to given data


So for any xi, (x_i − 62)² ≤ 140
⇒ x_i > 50∀i = 1, 2, 3,.....7
So no student is going to score less than 50.

Q.33. The mean and variance of 7 observations are 8 and 16 respectively. If two observations are 6 and 8, then the variance of the remaining 5 observations is :     (JEE Main 2021)
(a) 92/5
(b) 134/5
(c) 536/25
(d) 112/5

Ans. c
Let 8, 16, x₁, x₂, x₃, x_4, x₅ be the observations.
Now,

Also,

So variance of x₁, x₂, ......., x₅

Q.34. The mean and standard deviation of 20 observations were calculated as 10 and 2.5 respectively. It was found that by mistake one data value was taken as 25 instead of 35. if α and √β are the mean and standard deviation respectively for correct data, then (α, β) is :      (JEE Main 2021)
(a) (11, 26)
(b) (10.5, 25)
(c) (11, 25)
(d) (10.5, 26)

Ans. d
Given :

or Σx_i = 200 (incorrect)
or 200 − 25 + 35 = 210 = Σx_i (Correct)
Now correct
again given S.D = 2.5 (σ)



= 2725 (correct)
∴ correct σ² = (2725/20) − (10.5)²
σ² = 26
or σ = 26
∴ α = 10.5, β = 26

Q.35. If the mean and variance of the following data : 6, 10, 7, 13, a, 12, b, 12 are 9 and (37/4) respectively, then (a − b)² is equal to :     (JEE Main 2021)
(a) 24
(b) 12
(c) 32
(d) 16

Ans. d

60 + a + b = 72
a + b = 12 .....(1)

∑x_i² = 6² + 10² + 7² + 13² + a² + b² + 12² + 12² = a² + b² + 642




∴ a² + b² + 2ab = 144
80 + 2ab = 144
∴ 2ab = 64
∴ (a - b)² = a² + b² - 2ab = 80 - 64 = 16

Q.36. The first of the two samples in a group has 100 items with mean 15 and standard deviation 3. If the whole group has 250 items with mean 15.6 and standard deviation √13.44, then the standard deviation of the second sample is :      (JEE Main 2021)
(a) 8
(b) 6
(c) 4
(d) 5

Ans. c
n₁ = 100
m = 250


V₁(x) = 9
Var(x) = 13.44



⇒ σ₂² = 16 ⇒ σ₂ = 4

Q.37. Let the mean and variance of the frequency distribution

be 6 and 6.8 respectively. If x₃ is changed from 8 to 7, then the mean for the new data will be :      (JEE Main 2021)
(a) 4
(b) 5
(c) 17/3
(d) 16/3

Ans. c
Given 32 + 8α + 9β = (8 + α + β) × 6
⇒ 2α + 3β = 16 ..... (i)
Also, 4 × 16 + 4 × α + 9β = (8 + α + β) × 6.8
⇒ 640 + 40α + 90β = 544 + 68α + 68β
⇒ 28α − 22β = 96
⇒ 14α − 11β = 48 ..... (ii)
from (i) & (ii)
α = 5 & β = 2
So, new mean

Q.38. If the mean and variance of six observations 7, 10, 11, 15, a, b are 10 and 20/3, respectively, then the value of | a − b | is equal to :      (JEE Main 2021)
(a) 9
(b) 11
(c) 7
(d) 1

Ans. d

⇒ a + b = 17 ..... (i)

a² + b² = 145 ...... (ii)
Solve (i) and (ii) a = 9, b = 8 or a = 8, b = 9
|a − b| = 1

Q.39. The mean of 6 distinct observations is 6.5 and their variance is 10.25. If 4 out of 6 observations are 2, 4, 5 and 7, then the remaining two observations are :      (JEE Main 2021)
(a) 10, 11
(b) 3, 18
(c) 8, 13
(d) 1, 20

Ans. a
Let other two numbers be a, (21 − a)
Now,

(Using formula for variance)
⇒ 6(10.25) + 6(6.5)² = 94 + a² + (21−a)²
⇒ a² + (21−a)² = 221
∴ a = 10 and (21 − a) = 21 − 10 = 11
So, remaining two observations are 10, 11.
⇒ Option (1) is correct.

Q.40. Let in a series of 2n observations, half of them are equal to a and remaining half are equal to −a. Also by adding a constant b in each of these observations, the mean and standard deviation of new set become 5 and 20, respectively. Then the value of a² + b² is equal to :       (JEE Main 2021)
(a) 425
(b) 250
(c) 925
(d) 650

Ans. a
Given series
(a, a, a, ........ n times), (−a, −a, −a, ...... n times)

as, x_i → x_i + b


No change in S.D. due to change in origin
Standard deviation


∴ 20 = √a² ⇒ a = 20
∴ a² + b² = 425

Q.41. Consider three observations a, b, and c such that b = a + c. If the standard deviation of a + 2, b + 2, c + 2 is d, then which of the following is true?      (JEE Main 2021)
(a) b² = 3(a² + c²) + 9d²
(b) b² = 3(a² + c²) − 9d²
(c) b² = 3(a² + c² + d²)
(d) b² = a² + c² + 3d²

Ans. b
For a, b, c


We know, S.D. of a + 2, b + 2, c + 2 = S.D. of a, b, c = d

b² = 3a² + 3c² − 9d²

Q.42. Let X be a random variable with distribution.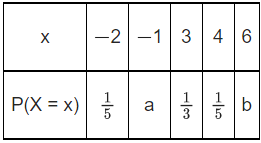

If the mean of X is 2.3 and variance of X is σ², then 100 σ² is equal to :     (JEE Main 2021)

Ans. 781


−a + 6b = (9/10) ..... (1)

a + b = (4/15) .... (2)
From equation (1) and (2)




= 4 + a + 3 + 36b − (2.3)²
= 7 + a + 36b − (2.3)²
= 7 + (1/10) + 6 − (2.3)²
= 13 + (1/10) − (2310)²
= 131/10 - (23/10)²
= (1310 − (23)²)/100
= ((1310 − 529)/100)
σ² = 781/100
100σ² = 781

Q.43. An online exam is attempted by 50 candidates out of which 20 are boys. The average marks obtained by boys is 12 with a variance 2. The variance of marks obtained by 30 girls is also 2. The average marks of all 50 candidates is 15. If μ is the average marks of girls and σ² is the variance of marks of 50 candidates, then μ + σ² is equal to ________.      (JEE Main 2021)

Ans. 25
σ_b² = 2 (variance of boys)
n₁ = no. of boys

n₂ = no. of girls

variance of combined series


σ² = 8
⇒ μ + σ² = 17 + 8 = 25

Q.44. Let n be an odd natural number such that the variance of 1, 2, 3, 4, ......, n is 14. Then n is equal to _______.      (JEE Main 2021)

Ans. 13

Q.45. Let the mean and variance of four numbers 3, 7, x and y(x > y) be 5 and 10 respectively. Then the mean of four numbers 3 + 2x, 7 + 2y, x + y and x − y is _______.       (JEE Main 2021)

Ans. 12


140 = 49 + 9 + x² + y²
x² + y² = 82
x + y = 10
⇒ (x, y) = (9, 1)
Four numbers are 21, 9, 10, 8
Mean = 48/4 = 12

Q.46. Consider the following frequency distribution :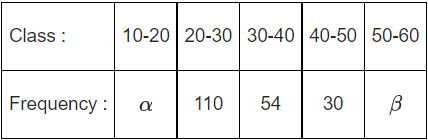

If the sum of all frequencies is 584 and median is 45, then | α − β | is equal to ________.     (JEE Main 2021)

Ans. 164
∵ Sum of frequencies = 584
⇒ α + β = 390
Now, median is at 584/2 = 292^th
∵ Median = 45 (lies in class 40 - 50)
⇒ α + 110 + 54 + 15 = 292
⇒ α = 113, β = 277
⇒ | α − β | = 164

Q.47. Consider the following frequency distribution :

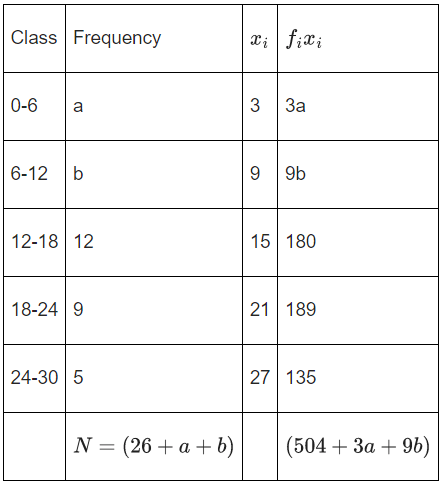
If mean = 309/22 and median = 14, then the value (a − b)² is equal to _______.      (JEE Main 2021)

Ans. 4


⇒ 66a + 198b + 11088 = 309a + 309b + 8034
⇒ 243a + 111b = 3054
⇒ 81a + 37b = 1018 → (1)
Now, Median


⇒ a + b = 18 → (2)
From equation (1) (2) a = 8, b = 10
∴ (a − b)² = (8 − 10)²$

Q.48. The mean age of 25 teachers in a school is 40 years. A teacher retires at the age of 60 years and a new teacher is appointed in his place. If the mean age of the teachers in this school now is 39 years, then the age (in years) of the newly appointed teacher is _______.       (JEE Main 2021)

Ans. 35
x₁ + x₂ +.....+ x₂₅ = 25 × 40 = 1000

⇒ 100 − 60 + a = 25 × 39
⇒ a = − 940 + 975
⇒ a = 35

Q.49. Consider a set of 3n numbers having variance 4. In this set, the mean of first 2n numbers is 6 and the mean of the remaining n numbers is 3. A new set is constructed by adding 1 into each of first 2n numbers, and subtracting 1 from each of the remaining n numbers. If the variance of the new set is k, then 9k is equal to ______.       (JEE Main 2021)

Ans. 68
Let first 2n observations are x₁, x₂ ...................., x_2n
and last n observations are y₁, y₂ ....................., y_n





Now, mean is
Now, variance is




⇒ 9k = 68
Therefore, the correct answer is 68.

Q.50. Consider the statistics of two sets of observations as follows :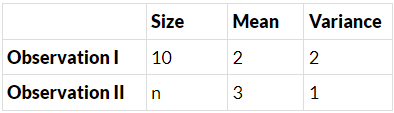

If the variance of the combined set of these two observations is (17/9), then the value of n is equal to ____.     (JEE Main 2021)

Ans. 5


For group - 2 :

Now, combined variance


⇒ 17 (n² + 20n + 100) = 9(n² + 40n + 200)
⇒ 8n² − 20n − 100 = 0
⇒ 2n² − 5n − 25 = 0 ⇒ n = 5

Q.51. Let X₁, X₂, ......., X₁₈ be eighteen observations such that 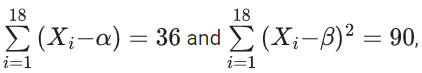 where α and β are distinct real numbers. If the standard deviation of these observations is 1, then the value of | α − β | is _______.        (JEE Main 2021)

Ans. 4

⇒ ∑x_i − 18α = 36
⇒ ∑x_i = 18(α+2) .... (1)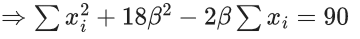

 
⇒ ∑x_i² + 18β² + 2β × 18(α+2) = 90 (using equation (1))
⇒ ∑x_i² = 90 − 18β² + 36β(α+2)


⇒ 90 − 18β² + 36αβ + 72β − 18(α+2)² = 18
⇒ 5 − β² + 2αβ + 4β − (α+2)² = 1
⇒ 5 − β² + 2αβ + 4β − α² − 4 − 4α = 1
⇒ α² − β² + 2αβ + 4β − 4α = 0
⇒ (α − β)(α − β + 4) = 0
⇒ α − β = −4
∴ |α − β| = 4 (α ≠ β)

Q.52. If the variance of 10 natural numbers 1, 1, 1, ....., 1, k is less than 10, then the maximum possible value of k is _____.     (JEE Main 2021)

Ans. 11


(90 + k²)10 − (81 + k² + 8k) < 1000
90 + 10k² − k² − 18k − 81 < 1000
9k² − 18k + 9 < 1000


k ≤ 11
Maximum integral value of k = 11.