Important Formulas: Coordinate Geometry | Mathematics (Maths) Class 9 PDF Download
Introduction
Coordinate geometry is essential in mathematics as it helps to visually show geometric shapes on a two-dimensional plane, improving our understanding of their properties. In this chapter, you will learn some basic ideas of coordinate geometry, which was first developed by the French philosopher and mathematician René Descartes. Coordinate Geometry
Coordinate Geometry
Coordinate Plane
The Cartesian plane, also known as the coordinate plane, splits the plane into two dimensions through the horizontal x-axis and the vertical y-axis. These axes create four sections called quadrants. This system allows us to pinpoint locations accurately, with the point of intersection known as the origin. The coordinates of the origin are (0, 0). 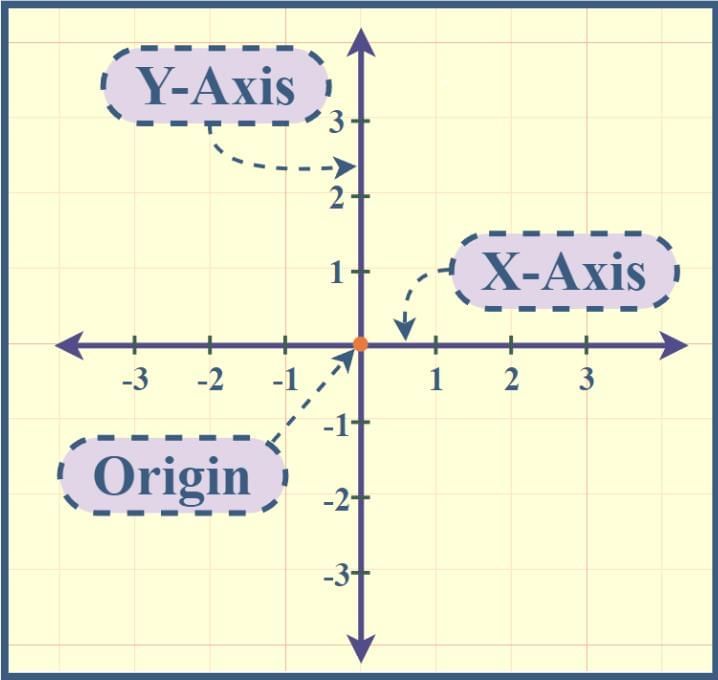
Points on the coordinate plane are represented as (x, y), where:
- The distance from the y-axis is the x-coordinate or abscissa.
- The distance from the x-axis is the y-coordinate or ordinate.

The coordinates in the different quadrants are represented as:
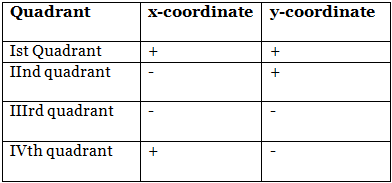
Locating points on the graph
To plot a point (x, y) on the Cartesian plane:
Identify the Coordinates: Determine the x and y values.
Locate the X-coordinate: Move along the x-axis to the x value.
Locate the Y-coordinate: Move parallel to the y-axis to the y value.
Find the Intersection: The point where the vertical line from the x-coordinate and the horizontal line from the y-coordinate meet is the location of (x, y).
Example:
To plot the point (2, 5):
X-coordinate: Move 2 units right from the origin along the x-axis.
Y-coordinate: Move 5 units up along the y-axis from the x-axis point.
Intersection: The point where these lines intersect is (2, 5).
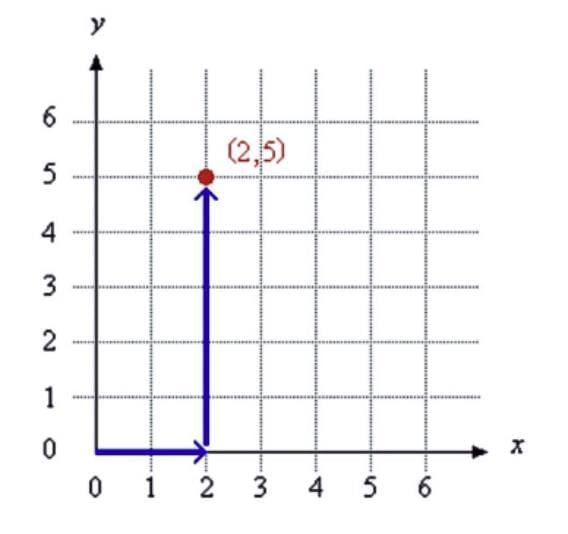
|
40 videos|471 docs|57 tests
|
FAQs on Important Formulas: Coordinate Geometry - Mathematics (Maths) Class 9
| 1. What is the Coordinate Plane and how is it structured? |  |
| 2. How do you calculate the distance between two points in the Coordinate Plane? |  |
| 3. What is the Slope Formula and why is it important? |  |
| 4. How can the Midpoint Formula be used in coordinate geometry? |  |
| 5. What is the formula for the area of a triangle in Coordinate Geometry? |  |

















