Important Definitions & Formulas: Coordinate Geometry | Mathematics (Maths) Class 10 PDF Download

Points on a Cartesian Plane
A pair of numbers locate points on a plane called the coordinates. The distance of a point from the y-axis is known as abscissa or x-coordinate. The distance of a point from the x-axis is called ordinate or y-coordinate.
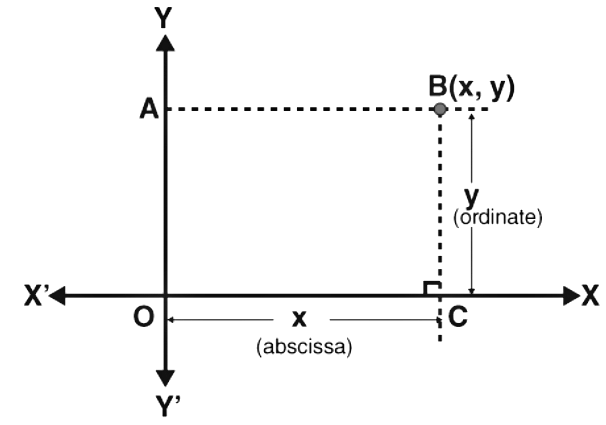
Example: Consider a point P(3, 2), where 3 is the abscissa, and 2 is the ordinate. 3 represents the distance of point P from the y-axis, and 2 represents the distance of point P from the x-axis.
Distance Formula
Distance between Two Points on the Same Coordinate Axes
The distance between two points that are on the same axis (x-axis or y-axis) is given by the difference between their ordinates if they are on the y-axis, else by the difference between their abscissa if they are on the x-axis.
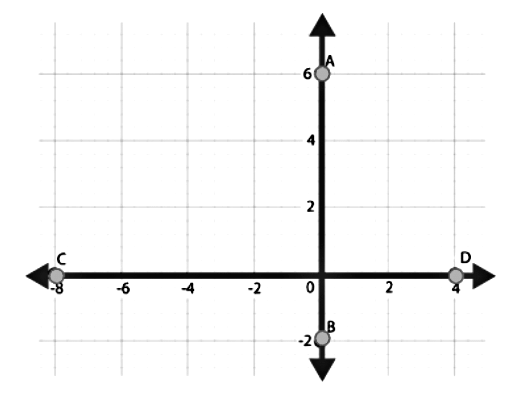
Distance AB = 6 – (-2) = 8 units
Distance CD = 4 – (-8) = 12 units
Distance between Two Points Using Pythagoras Theorem
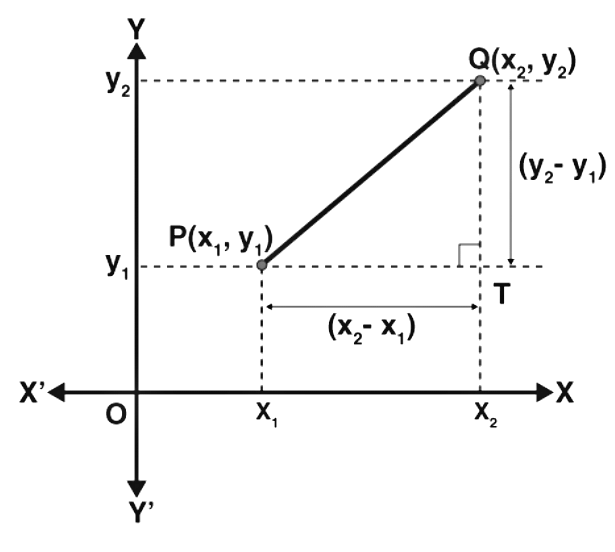
Let P(x1, y1) and Q(x2, y2) be any two points on the cartesian plane.
Draw lines parallel to the axes through P and Q to meet at T.
ΔPTQ is right-angled at T.
By Pythagoras Theorem,
PQ2 = PT2 + QT2
= (x2 – x1)2 + (y2 – y1)2
PQ = √[x2 – x1)2 + (y2 – y1)2]
Distance Formula: Distance between any two points (x1, y1) and (x2, y2) is given by
 Where d is the distance between the points (x1,y1) and (x2,y2).
Where d is the distance between the points (x1,y1) and (x2,y2).
Section Formula
If the point P(x, y) divides the line segment joining A(x1, y1) and B(x2, y2) internally in the ratio m1:m2, then, the coordinates of P are given by the section formula as:

Finding Ratio given the points
To find the ratio in which a given point P(x, y) divides the line segment joining A(x1, y1) and B(x2, y2),
- Assume that the ratio is k : 1
- Substitute the ratio in the section formula for any of the coordinates to get the value of k.
 When x1, x2 and x are known, k can be calculated. The same can be calculated from the y- coordinate also.
When x1, x2 and x are known, k can be calculated. The same can be calculated from the y- coordinate also.
Example: Find the ratio when point (– 4, 6) divide the line segment joining the points A(– 6, 10) and B(3, – 8)?
Solution: Let the ratio be m:n.
We can write the ratio as:
m/n : 1 or k:1
Suppose (-4, 6) divide the line segment AB in k:1 ratio.
Now using the section formula, we have the following;

-4 = (3k-6)/(k+1)
– 4k – 4 = 3k – 6
7k =2
k:1 = 2:7
Thus, the required ratio is 2:7.
Midpoint
The midpoint of any line segment divides it in the ratio 1:1.

The coordinates of the midpoint(P) of line segment joining A(x1, y1) and B(x2, y2) is given by 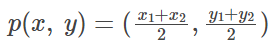
Example: What is the midpoint of line segment PQ whose coordinates are P (-3, 3) and Q (1, 4), respectively.
Solution: Given, P (-3, -3) and Q (1, 4) are the points of line segment PQ.
Using midpoint formula, we have;
= (-2/2, 1/2)
= (-1, 1/2)
Points of Trisection
To find the points of trisection P and Q, which divides the line segment joining A(x1, y1) and B(x2, y2) into three equal parts:
i) AP : PB = 1 : 2
ii) AQ : QB = 2 : 1 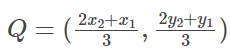
Example: Find the coordinates of the points of trisection of the line segment joining the points A(2, – 2) and B(– 7, 4).
Solution: Let P and Q divide the line segment AB into three parts.
So, P and Q are the points of trisection here.
Let P divides AB in 1:2, thus by section formula, the coordinates of P are (1, 0)
Let Q divides AB in 2:1 ratio, then by section formula, the coordinates are (-4,2)
Thus, the point of trisection for line segment AB are (1,0) and (-4,2).
Centroid of a Triangle
If A(x1, y1), B(x2, y2), and C(x3, y3) are the vertices of a ΔABC, then the coordinates of its centroid(P) are given by
Example: Find the coordinates of the centroid of a triangle whose vertices are given as (-1, -3), (2, 1) and (8, -4)
Solution: Given,
The coordinates of the vertices of a triangle are (-1, -3), (2, 1) and (8, -4)
The Centroid of a triangle is given by: Therefore, the centroid of a triangle, G = (3, -2)
Therefore, the centroid of a triangle, G = (3, -2)
Area from Coordinates
Area of a Triangle given its vertices
If A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of a Δ ABC, then its area is given by Where A is the area of the Δ ABC.
Where A is the area of the Δ ABC.
Example: Find the area of the triangle ABC whose vertices are A(1, 2), B(4, 2) and C(3, 5).
Solution:
Using the formula given above, Area = 9/2 square units.
Area = 9/2 square units.
Therefore, the area of a triangle ABC is 9/2 square units.
To know more about the Area of a Triangle,
Collinearity Condition
If three points A, B and C are collinear and B lies between A and C, then,
- AB + BC = AC. AB, BC, and AC can be calculated using the distance formula.
- The ratio in which B divides AC, calculated using the section formula for both the x and y coordinates separately, will be equal.
- The area of a triangle formed by three collinear points is zero.
|
127 videos|665 docs|84 tests
|
FAQs on Important Definitions & Formulas: Coordinate Geometry - Mathematics (Maths) Class 10
| 1. What is the distance formula used to calculate the distance between two points on a Cartesian plane? |  |
| 2. How do you find the midpoint of a line segment between two points? |  |
| 3. What is the section formula and how is it used to find the coordinates of a point dividing a line segment in a given ratio? |  |
| 4. What is the condition for three points to be collinear on a Cartesian plane? |  |
| 5. How can I find the centroid of a triangle given its vertices? |  |






















