Electronics and Communication Engineering (ECE) Exam > Electronics and Communication Engineering (ECE) Notes > Digital Circuits > Binary to Excess-3 & Excess-3 to Binary Conversion
Binary to Excess-3 & Excess-3 to Binary Conversion | Digital Circuits - Electronics and Communication Engineering (ECE) PDF Download
Introduction
The excess-3 code plays an important role in representing the decimal numbers. The Excess-3 code can also be represented as the XS-3 code. In Excess-3 code, each digit of the decimal number is represented by adding 3 in each decimal digit. There are the following steps to convert the binary number into Excess-3 code:
- Convert the binary number into decimal.
- Add 3 in each digit of the decimal number.
- Find the binary code of each digit of the newly generated decimal number.
We can also add 0011 in each 4-bit BCD code of the decimal number for getting excess-3 code.
Let's take an example to understand the process of converting a binary number into Excess-3 code.
Example 1: Convert (11110)2 to Excess-3 using binary
1. First, convert the given binary number into a decimal number.
Binary Number: (11110)2
Finding Decimal Equivalent of the number: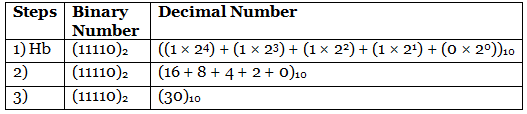
Decimal number of the Binary number (11110)2 is (30)10
2. Now, we add 3 in each digit of the decimal number.
The decimal number is 30. Now, we will add 3 into the decimal number 30.
= 30 + 33
= 63
3. Now, we find the binary code of each digit of the decimal number 63.
We write the binary code of each decimal digit in order to get Excess-3 code as: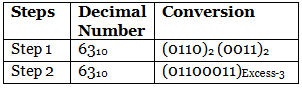
Result:
(11110)2 = (01100011)Excess-3
Below is the table that contains the excess-3 code of the decimal and BCD.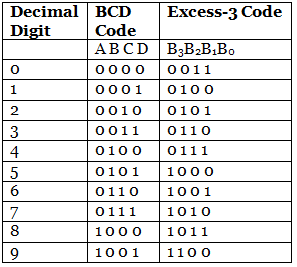
In the above table, the most significant bit of the decimal number is represented by the bit B3, and the least significant bits are represented by B2, B1, and B0.
Excess-3 to Binary Conversion
The process of converting Excess-3 code into binary is opposite to the process of converting Binary code into Excess-3. There are the following steps to convert the Excess-3 code into binary:
- In the first step, we will make the group of 4 bits and write the equivalent decimal number from the Excess-3 table.
- At last, we find the binary number of the decimal number using a decimal to binary conversion.
Example 1: (01100011)Excess-3
1. Making groups of four bits and write their equivalent decimal number.
(01100011)Excess-3 = (0110 0011)Excess-3
From the Excess-3 table:
(0110)Excess-3 = (3)10
(0011)Excess-3 = (0)10
So, the decimal number of excess-3 code 01100011 is: (30)10
2. Find the binary number.
Now, find the binary number of the decimal number (30)10 using a decimal to binary conversion as:
Divide the number 30 and its successive quotients with base 2.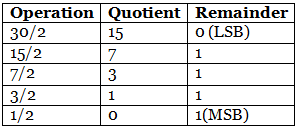
(30)10 = (11110)2
So, the binary number of excess-3 code 01100011 is: (11110)2
The document Binary to Excess-3 & Excess-3 to Binary Conversion | Digital Circuits - Electronics and Communication Engineering (ECE) is a part of the Electronics and Communication Engineering (ECE) Course Digital Circuits.
All you need of Electronics and Communication Engineering (ECE) at this link: Electronics and Communication Engineering (ECE)
|
75 videos|145 docs|70 tests
|
Related Exams
About this Document
4.78/5
Rating
Apr 13, 2025
Last updated
Document Description: Binary to Excess-3 & Excess-3 to Binary Conversion for Electronics and Communication Engineering (ECE) 2025 is part of Digital Circuits preparation.
The notes and questions for Binary to Excess-3 & Excess-3 to Binary Conversion have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. Information about Binary to Excess-3 & Excess-3 to Binary Conversion covers topics
like Introduction and Binary to Excess-3 & Excess-3 to Binary Conversion Example, for Electronics and Communication Engineering (ECE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Binary to Excess-3 & Excess-3 to Binary Conversion.
Introduction of Binary to Excess-3 & Excess-3 to Binary Conversion in English is available as part of our Digital Circuits
for Electronics and Communication Engineering (ECE) & Binary to Excess-3 & Excess-3 to Binary Conversion in Hindi for Digital Circuits course.
Download more important topics related with notes, lectures and mock test series for Electronics and Communication Engineering (ECE)
Exam by signing up for free. Electronics and Communication Engineering (ECE): Binary to Excess-3 & Excess-3 to Binary Conversion | Digital Circuits - Electronics and Communication Engineering (ECE)
Description
Full syllabus notes, lecture & questions for Binary to Excess-3 & Excess-3 to Binary Conversion | Digital Circuits - Electronics and Communication Engineering (ECE) - Electronics and Communication Engineering (ECE) | Plus excerises question with solution to help you revise complete syllabus for Digital Circuits | Best notes, free PDF download
Information about Binary to Excess-3 & Excess-3 to Binary Conversion
In this doc you can find the meaning of Binary to Excess-3 & Excess-3 to Binary Conversion defined & explained in the simplest way possible. Besides explaining types of
Binary to Excess-3 & Excess-3 to Binary Conversion theory, EduRev gives you an ample number of questions to practice Binary to Excess-3 & Excess-3 to Binary Conversion tests, examples and also practice Electronics and Communication Engineering (ECE)
tests
Related Searches
Exam
,MCQs
,Important questions
,video lectures
,mock tests for examination
,Binary to Excess-3 & Excess-3 to Binary Conversion | Digital Circuits - Electronics and Communication Engineering (ECE)
,Summary
,Viva Questions
,ppt
,Binary to Excess-3 & Excess-3 to Binary Conversion | Digital Circuits - Electronics and Communication Engineering (ECE)
,Sample Paper
,Extra Questions
,Free
,practice quizzes
,Semester Notes
,Binary to Excess-3 & Excess-3 to Binary Conversion | Digital Circuits - Electronics and Communication Engineering (ECE)
,study material
,Objective type Questions
,Previous Year Questions with Solutions
,past year papers
,shortcuts and tricks
;x![]()
For Your Perfect Score in Electronics and Communication Engineering (ECE)
The Best you need at One Place
Additional Information about Binary to Excess-3 & Excess-3 to Binary Conversion for Electronics and Communication Engineering (ECE) Preparation
Binary to Excess-3 & Excess-3 to Binary Conversion Free PDF Download
The Binary to Excess-3 & Excess-3 to Binary Conversion is an invaluable resource that delves deep into the core of the Electronics and Communication Engineering (ECE) exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Binary to Excess-3 & Excess-3 to Binary Conversion now and kickstart your journey towards success in the Electronics and Communication Engineering (ECE) exam.
Importance of Binary to Excess-3 & Excess-3 to Binary Conversion
The importance of Binary to Excess-3 & Excess-3 to Binary Conversion cannot be overstated, especially for Electronics and Communication Engineering (ECE) aspirants.
This document holds the key to success in the Electronics and Communication Engineering (ECE) exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Binary to Excess-3 & Excess-3 to Binary Conversion Notes
Binary to Excess-3 & Excess-3 to Binary Conversion Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Binary to Excess-3 & Excess-3 to Binary Conversion.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Binary to Excess-3 & Excess-3 to Binary Conversion Notes on EduRev are your ultimate resource for success.
Binary to Excess-3 & Excess-3 to Binary Conversion Electronics and Communication Engineering (ECE) Questions
The "Binary to Excess-3 & Excess-3 to Binary Conversion Electronics and Communication Engineering (ECE) Questions" guide is a valuable resource for all aspiring students preparing for the
Electronics and Communication Engineering (ECE) exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Binary to Excess-3 & Excess-3 to Binary Conversion on the App
Students of Electronics and Communication Engineering (ECE) can study Binary to Excess-3 & Excess-3 to Binary Conversion alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Binary to Excess-3 & Excess-3 to Binary Conversion,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Binary to Excess-3 & Excess-3 to Binary Conversion is prepared as per the latest Electronics and Communication Engineering (ECE) syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup