Product of Sum | Digital Circuits - Electronics and Communication Engineering (ECE) PDF Download
Introduction
A canonical product of sum is a boolean expression that entirely consists of maxterms. The Boolean function F is defined on two variables X and Y. The X and Y are the inputs of the boolean function F whose output is true when only one of the inputs is set to true. The truth table for Boolean expression F is as follows: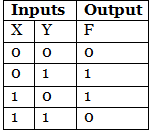 In our minterm and maxterm section, we learned about how we can form the maxterm from the variable's value. A column will be added for the maxterm in the above table. The complement of the variables is taken whose value is 0, and the variables whose value is 1 will remain the same.
In our minterm and maxterm section, we learned about how we can form the maxterm from the variable's value. A column will be added for the maxterm in the above table. The complement of the variables is taken whose value is 0, and the variables whose value is 1 will remain the same.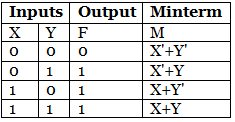
Now, we will multiply all the minterms for which the output is false to find the desired canonical POS(Product of sum) expression.
F = (X' + Y').(X + Y)
Converting Product of Sum (POS) to shorthand notation
The process of converting POS form to shorthand notation is the same as the process of finding shorthand notation for maxterms. There are the following steps used to find the shorthand notation of the given POS expression.
- Write the given POS expression.
- Find the shorthand notation of all the maxterms.
- Replace the minterms with their shorthand notations in the given expression.
Example: F = (X'+Y').(X+Y)
1. Firstly, we will write the POS expression:
F = (X'+Y').(X+Y)
2. Now, we will find the shorthand notations of the maxterms X' + Y' and X + Y.
X'+Y' = (00)2 = M0
X+Y = (11)2 = M3
3. In the end, we will replace all the minterms with their shorthand notations:
F = M0.M3
Converting shorthand notation to POS expression
The process of converting shorthand notation to POS is the reverse process of converting POS expression to shorthand notation. Let's see an example to understand this conversion.
Example:
Let us assume that we have a boolean function F, defined on two variables X and Y. The maxterms for the function F are expressed as shorthand notation is as follows:
F = ∏(1, 2, 3)
Now, from this expression, we find the POS expression. The Boolean function F has two input variables X and Y and the output of F = 0 for M1, M2, and M3, i.e., 1st, 2nd, and 3rd combinations. So,
F = ∏(1,2,3)
F = M1.M2.M3
F = 01.10.11
Next, we replace zeros with either X or Y and ones with either X' or Y'. Simply, if the value of the variable is 1, then we take the complement of that variable, and if the value of the variable is 0, then we take the variable "as is".
F = ∑(1,2,3)
F = 01.10.11
F = (A+B').( A'+B).( A'+B')
|
75 videos|188 docs|70 tests
|
















