What are Functions? | Mathematics for Digital SAT PDF Download

Introduction

• A function is a process or a relation that associates each element 'a' of a non-empty set A , at least to a single element 'b' of another non-empty set B. A relation f from a set A (the domain of the function) to another set B (the co-domain of the function) is called a function in math. f = {(a,b)| for all a ∈ A, b ∈ B}
  • A relation is said to be a function if every element of set A has one and only one image in set B.
  • A function is a relation from a non-empty set B such that the domain of a function is A and no two distinct ordered pairs in f have the same first element.
  • A function from A → B and (a, b) ∈ f, then f(a) = b, where 'b' is the image of 'a' under 'f' and 'a' is the preimage of 'b' under 'f'.
  • If there exists a function f: A → B, the set A is called the domain of the function f, and the set B is called its co-domain.

Examples of Functions

• Whenever we say that a variable quantity y is a function of a variable quantity x, we mean to say that: y depends on x; the value of y is determined by the value of x. We can write this dependence as follows: y = f(x)
  • The area of a circle can be expressed in terms of its radius A = π r². Area A is dependent on the radius r. In the language of functions in math, we say that A is a function of r.
  • The volume V of a sphere is a function of its radius. The dependence of V on r is given by V = 4/3 π r³.
  • The acceleration a of a body of fixed mass m is a function of the force F applied on the body: a = F/m.
  • The power P dissipated in a resistor of fixed resistance R is a function of the current I passing through the resistor: P = I²R
  • Suppose that a taxi charges a down payment of $10, and subsequently, $ 2 for every mile traveled. The taxi fare F is a function of the distance d traveled, and the dependence between the two quantities is given by F = 10 + 2d (F is in dollars and d is in miles).

Representation of Functions in Math

• The rule which specifies a function can come in many different forms based on how it is defined. They can be defined as piecewise-defined-functions or as formulas. When we define f(x) = √x, for x ≥ 0, then the inputs are the numbers that we provide and the 'taking square root' function accepts all non-negative real numbers and gets the output as f(x). Most often it is a formula, as in
  
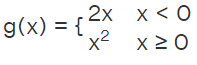
• where the domain of g = all real numbers
• A function in math can be represented as:
  • a set of ordered pairs
  • an arrow diagram
  • a table form
  • a graphical form

"f(x) = x² " is the general manner to represent a function. It is said as f of x is equal to x square. This is represented as f = {(1,1), (2,4), (3,9)}. The domain and range of a function is given as D= {1, 2, 3}, R={1,4, 9}. Here is a representation of a function in math as an ordered pair.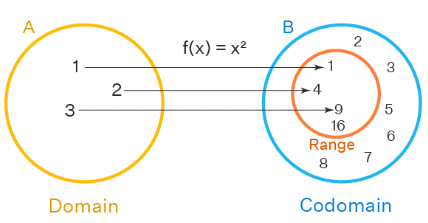

Function in math

Identification of a Function in Math

• A function in math means a correspondence from one value x of the first set to another value y of the second set. This correspondence can be of the following four types. But every correspondence is not a function. 
• In the example below, only 1 – 1 and many to one are examples of a function because no two ordered pairs have the same first component and all elements of the first set are linked in them. So we say that in a function one input can result in only one output. If we are given any x then there is one and only one y that can be paired with that x. A function cannot be associated with two outputs. A curve drawn in a graph is represented as a function, then every vertical line intersects the curve in at most one point. This vertical line test helps us in determining whether the curve is a function or not.

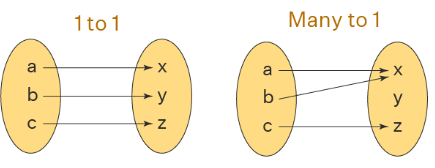
Function

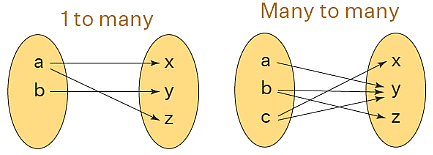
Non-Function

Types of Functions

• Functions in math have paramount importance and let us study different types of functions. We have four functions based on the mapping of elements from set A to set B.
  • f: A → B is said to be one-to-one or injective, if the images of distinct elements of A under f are distinct, i.e, for every a, b in A, f(a) = f(b), ⇒ a = b. Otherwise, it is many-to-one.
  • f: A → B is said to be onto, if every element of B is the image of some element of A under f, i.e, for every b ϵ B, there exists an element a in A such that f(a) = b. A function is onto if and only if the range of the function = B.
  • f: A → B is said to be one-to-one and onto or bijective, if f is both one-one and onto.

Composition of Functions

• Let f : A → B and g: B→ C be two functions. Then the composition of f and g is denoted as f(g) and it is defined as the function f ∘ g = f(g(x)) for x ∈ A. Let us consider an example of two functions f(x) and g(x). Let f(x) = (x+1) and g(x) = x². Then f ∘ g = f(x²)
  f(x²) = x² + 1
  g ∘ f = g(f(x))
  g(f(x)) = g((x+1))
  = (x+1)² = x² + 2x + 1
• Thus we can conclude that the composition of functions is not commutative. f ∘ g ≠ g ∘ f

Algebra of Functions

• The algebra of functions deals with the operations of functions. For the functions f(x) and g(x), where f: X → R and g: X → R, where x ϵ X, we have:
  • (f+g) (x) = f(x) + g(x)
  • (f-g) (x) = f(x) - g(x)
  • (f.g) (x) = f(x) .g(x)
  • (k f(x)) = k (f(x)), where k is a real number
  • (f/g)(x) = f(x) /g(x), where g(x) ≠ 0

Graphing Functions

• The various types of functions are identity function, constant function, quadratic function, cubic function, cube root function, rational function, modulus function, and so on. Graphing functions is done by placing the independent variable on the x-axis and the dependent variable on the y-axis and plotting the points with coordinates (x,y) in the cartesian plane. All the points on the graph satisfy the equation y = f(x).
  
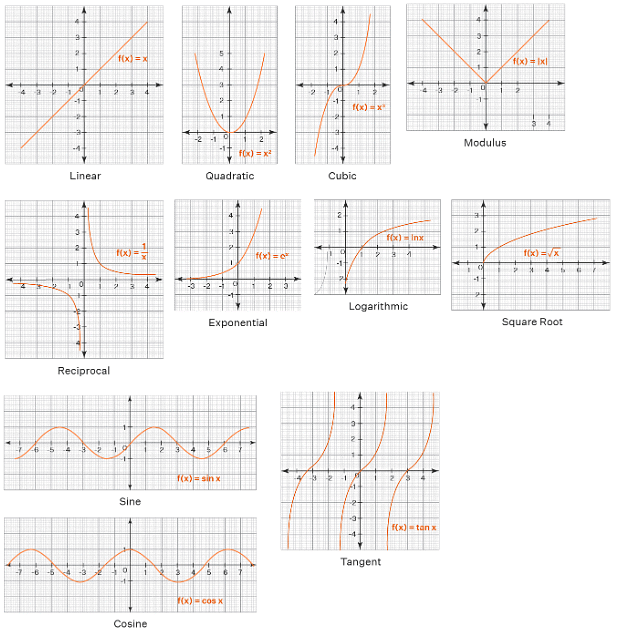
  • The identity function is the type of function which gives the same input as the output. It is expressed as, f(x) = x, where x ϵ R. For example, f(3) = 3 is an identity function.
  • A constant function is the type of function which gives the same value of output for any given input. It is expressed as, f(x) = c, where c is a constant. For example, f(x) = 2 is a constant function.
  • A Polynomial function is a type of function which can be expressed as a polynomial. It is expressed as,
    f(x) = a_nxⁿ + a_{n − 1} x^{n − 1} + . . . . . . . + a₀x₀ . For example, f(x) = 2x+5 is a polynomial function. f(x)= x³ - 6x² + 11x - 6
  • A Quadratic function is a type of function which has the highest power 2 in the polynomial function. It is expressed as, f(x) = a(x-h)² + k. For example, f(x) = x² + 1 is a quadratic function. The following figure shows the plot of a quadratic function.
  • A cubic function is a type of function which has the highest power 3 in the polynomial function.It is expressed as, f(x) = ax³ + bx² + cx + d, where a, b, c, d are constants. For example, f(x) = x³ + 4 is a cubic function. The following figure shows the plot of a cubic function.
  • A Rational function is a type of function which is derived from the ratio of two polynomial functions. It is expressed as, f(x) = P(x)/Q(x), such that P and Q are polynomial functions of x and Q(x) ≠ 0. For example,
    fx =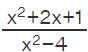
  • Modulus function is a type of function which gives the absolute value of a number by giving its magnitude. It is expressed as, f(x) = |x| It can further be defined as:
    

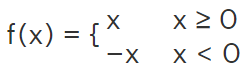
Important Notes

• A function in math means a correspondence from one value x of the first set A to another value y of the second set B. It relates inputs to outputs.
• Functions in maths are the subsets of relations.
• If A and B are finite sets such that n(A) = p and n(B) =q, then the total number of functions that exist from A → B is q^p
• Special Rules: 
  • A function must work for all the possible input values 
  • With each input value, it must have one relationship only. 
  • every element in the domain of 'f' has only an image.

Functions Examples

Example 1: Given two functions f and g as, f (x) = √(x - 2) and g (x) = ln( 1 + x²). Find the composite function (g ∘f )(x).

Given: functions f(x) and g(x).

(g ∘ f )( x ) = g ( f (x))
Since f (x) =√(x - 2), substituting x = f (x), we get,
(g ( f (x)) = ln( 1+ f (x)2)
= ln( 1 +√(x - 2) 2)
= ln(1 + ( x - 2 ))
= ln((x - 1))
∴ (g ∘ f )( x ) = ln(x - 1)

Example 2: The length of a rectangle is twice that of its breadth. Express the area of the rectangle as a function of its (i) length (ii) diagonal length.

(i) In terms of the length l,the area A is
A = f( l ) = l × l/2 = l²/2
(ii) The diagonal length d is given be
d² = l² + l² /4  = 5l²/4
Thus,
l =2d/ √5, b = l/2 =d/ √5
Now, the area A can be expressed as a function of d, as follows:
A = g( d) = lb = 2d/ √5 × d/ √5
=2d²/5
Area as a function of length = l²/2 and Area as a function of diagonal length = 2d²/5

Example 3: A cone has a variable height h and a variable base radius r, but the sum of h and r is fixed. The cone is made of a material of density ρ. Express the mass m of the cone as a function of its height h.

The volume V of a cone is given by:
V = 1/3 π r²h
Let the (fixed) sum of h and r be k. Thus, r = k - h, and so:
V = 1/3 π h(k-h)²
The mass of the cone can now we expressed as a function of h; m will be ρ times the volume V:
m = f(h) = ρ V
m = 1/3 π ρ h(k-h)²
m = 1/3 π ρ h(k-h)² is the required function definition.