Syntax Tree | Compiler Design - Computer Science Engineering (CSE) PDF Download

Clear all your Computer Science Engineering (CSE) doubts with EduRev Join for Free

Join for Free

Introduction

Tree in which each leaf node describes an operand & each interior node an operator. The syntax tree is shortened form of the Parse Tree.

Example 1: Draw Syntax Tree for the string a + b ∗ c − d.
Rules for constructing a syntax tree
Each node in a syntax tree can be executed as data with multiple fields. In the node for an operator, one field recognizes the operator and the remaining field includes a pointer to the nodes for the operands. The operator is known as the label of the node. The following functions are used to create the nodes of the syntax tree for the expressions with binary operators. Each function returns a pointer to the recently generated node.

• mknode (op, left, right): It generates an operator node with label op and two field including pointers to left and right.
• mkleaf (id, entry): It generates an identifier node with label id and the field including the entry, a pointer to the symbol table entry for the identifier.
• mkleaf (num, val): It generates a number node with label num and a field including val, the value of the number. For example, construct a syntax tree for an expression a − 4 + c. In this sequence, p₁, p₂, … . . p₅ are pointers to the symbol table entries for identifier 'a' and 'c' respectively.

p₁− mkleaf (id, entry a);

p₂ − mkleaf (num, 4);

p₃ − mknode ( ′−′, p₁, p₂)

p₄ − mkleaf(id, entry c)

p₅ − mknode(′+′, p₃, p₄);

The tree is generated in a bottom-up fashion. The function calls mkleaf (id, entry a) and mkleaf (num 4) construct the leaves for a and 4. The pointers to these nodes are stored using p₁ and p₂. The call mknodes (′−′, p₁, p₂) then make the interior node with the leaves for a and 4 as children. The syntax tree will be

Syntax Directed Translation of Syntax Trees

Node (+, 𝐄^(𝟏), 𝐕𝐀𝐋, 𝐄^(𝟐). 𝐕𝐀𝐋) will create a node labeled +.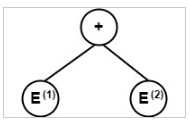
E⁽¹⁾. VAL &E⁽²⁾. VAL are left & right children of this node.
Similarly, Node (∗, E⁽¹⁾. VAL, E⁽²⁾. VAL) will make the syntax as −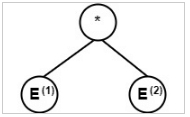
Function UNARY (−, E⁽¹⁾. VAL)will make a node – (unary minus) & E⁽¹⁾. VAL will be the only child of it.
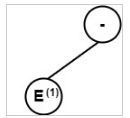Function LEAF (id) will create a Leaf node with label id.

Example 2: Construct a syntax tree for the expression.
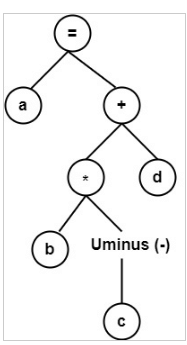
a = b ∗ −c + d

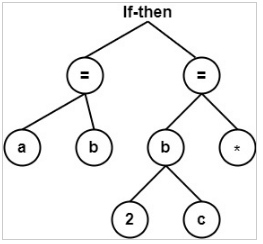
Example 3: Construct a syntax tree for a statement.
If a = b then b = 2 * c

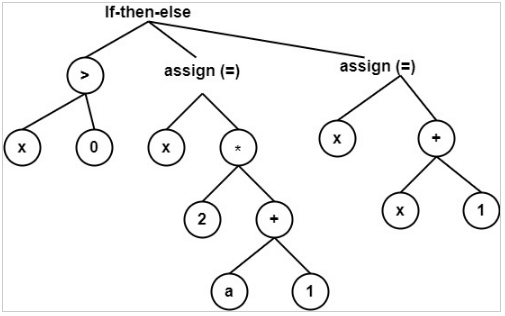
Example 4: Consider the following code. Draw its syntax Tree
If x > 0 then x = 2 * (a + 1) else x = x + 1.

Example 5: Draw syntax tree for following arithmetic expression a * (b + c) – d /2. Also, write given expression in postfix form.

Postfix Notation
a b c + * d 2 / -