Class 10 Exam > Class 10 Notes > The Complete SAT Course > Number Set Theory
Number Set Theory | The Complete SAT Course - Class 10 PDF Download
Introduction
- Sets in mathematics, are simply a collection of distinct objects forming a group. A set can have any group of items, be it a collection of numbers, days of a week, types of vehicles, and so on. Every item in the set is called an element of the set. Curly brackets are used while writing a set. A very simple example of a set would be like this. Set A = {1,2,3,4,5}. There are various notations to represent elements of a set. Sets are usually represented using a roster form or a set builder form.
Sets Definition
- In mathematics, a set is a well-defined collection of objects. Sets are named and represented using a capital letter. In the set theory, the elements that a set comprises can be any kind of thing: people, letters of the alphabet, numbers, shapes, variables, etc.
Sets in Maths Examples
We know that a collection of even natural numbers less than 10 is defined, whereas collection of intelligent students in a class is not defined. Thus, collection of even natural numbers less than 10 can be represented in the form of a set, A = {2, 4, 6, 8}. Let us use this example to understand the basic terminology associated with sets in math.
1. Elements of a Set
- The items present in a set are called either elements or members of a set. The elements of a set are enclosed in curly brackets separated by commas. To denote that an element is contained in a set, the symbol '∈' is used. In the above example, 2 ∈ A. If an element is not a member of a set, then it is denoted using the symbol '∉'. Here, 3 ∉ A.
2. Cardinal Number of a Set
- The cardinal number, cardinality, or order of a set denotes the total number of elements in the set. For natural even numbers less than 10, n(A) = 4. Sets are defined as a collection of unique elements. One important condition to define a set is that all the elements of a set should be related to each other and share a common property. For example, if we define a set with the elements as the names of months in a year, then we can say that all the elements of the set are the months of the year.
Representation of Sets
There are different set notations used for the representation of sets. They differ in the way in which the elements are listed. The three set notations used for representing sets are:
- Semantic Form: The semantic notation describes a statement to show what are the elements of a set. For example, Set A is the list of the first five odd numbers.
- Roster Form: The most common form used to represent sets is the roster notation in which the elements of the sets are enclosed in curly brackets separated by commas. For example, Set B = {2,4,6,8,10}, which is the collection of the first five even numbers. In a roster form, the order of the elements of the set does not matter, for example, the set of the first five even numbers can also be defined as {2,6,8,10,4}. Also, if there is an endless list of elements in a set, then they are defined using a series of dots at the end of the last element. For example, infinite sets are represented as, X = {1, 2, 3, 4, 5 ...}, where X is the set of natural numbers. To sum up the notation of the roster form, please take a look at the examples below.
- Finite Roster Notation of Sets : Set A = {1, 2, 3, 4, 5} (The first five natural numbers)
- Infinite Roster Notation of Sets : Set B = {5, 10, 15, 20 ....} (The multiples of 5)
- Set Builder Form: The set builder notation has a certain rule or a statement that specifically describes the common feature of all the elements of a set. The set builder form uses a vertical bar in its representation, with a text describing the character of the elements of the set. For example, A = { k | k is an even number, k ≤ 20}. The statement says, all the elements of set A are even numbers that are less than or equal to 20. Sometimes a ":" is used in the place of the "|".
Visual Representation of Sets Using Venn Diagram
- Venn Diagram is a pictorial representation of sets, with each set represented as a circle. The elements of a set are present inside the circles. Sometimes a rectangle encloses the circles, which represents the universal set. The Venn diagram represents how the given sets are related to each other.
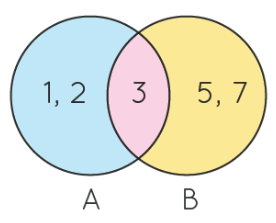
Set A = {1, 2, 3}
Set B = {3, 5, 7}
Elements of set A are 1, 2, 3
Element of set B are 3, 5, 7
Common element of set A and B is 3.
Sets Symbols
- Set symbols are used to define the elements of a given set. The following table shows some of these symbols and their meaning.

The document Number Set Theory | The Complete SAT Course - Class 10 is a part of the Class 10 Course The Complete SAT Course.
All you need of Class 10 at this link: Class 10
|
433 videos|220 docs|166 tests
|
Related Searches
















