NFA to Regular Expression | Theory of Computation - Computer Science Engineering (CSE) PDF Download

Introduction

NFA (Non-Deterministic Finite Automata) is a state machine used to validate an input string using state transitions. Regular expressions are a sequence of characters that are used to check if the given string follows the pattern or not. Both NFA and regular expressions can be used to define a regular language. In this article, we will see how to convert a given NFA to a regular expression.

Algorithm

Let there be an NFA with N states. Our task is to convert NFA to a regular expression. To do this, we will write equations for each state of the given NFA in the form:
q₁ = q₁a₁₁ + q₂a₂₁ + q₃a₃₁ + … qnan1
q₂ = q₁a₁₂ + q₂a₂₂ + q₃a₃₂ + … qnan₂
…
q_n = q₁a₁n + q₂a₂n + q₃a₃n + … qnann
In the above equations, qi is a state variable corresponding to the ith state, and aij is a set of input symbols.
After this, we try to represent qi in terms of aij using Arden’s Theorem and substituting the state variables. To convert the NFA to a regular expression, we then take the union of all the state variables corresponding to the final states.

Example: Consider the following NFA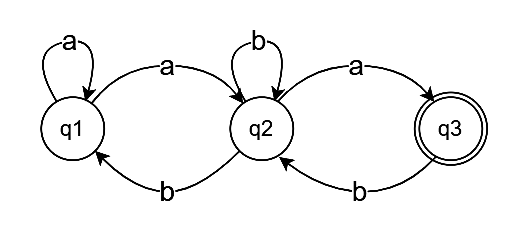

The above NFA has 3 states - q₁, q₂, q₃. To convert this NFA to a regular expression, we will first write the equations of all the states:
q1 = ϵ + q1a + q2b - (1)
q₂ = q₁a + q₂b + q₃b - (2)
q₃ = q₂a - (3)
Now we will simplify the above equations.
From (3):
q₃ = q₂a
= (q₁a + q₂b + q₃b)a
= q₁aa + q₂ba + q₃ba - (4)
From (2):
q₂ = q₁a + q₂b + q₃b
= q₁a + q₂b + (q₂a)b
= q₁a + q₂(b + ab)

According to Arden’s theorem, whenever we have an equation of the form R = Q + RP, it can be written as R = QP*.
q₂ = q₁a + q₂(b + ab) is of the form R = Q + RP, where R = q₂, Q = q₁a and P = (b + ab), therefore, we can write it as:
q₂ = q₁a(b + ab)* - (5)
From (1):
q₁ = ϵ + q1a + q₂b
Putting value of q₂ from equation (5):
q₁ = ϵ + q₁a + (q₁a(b + ab)*)b
q₁ = ϵ + q₁(a + (a(b + ab)*)b
Now, this equation is again of the form R = Q + RP, where R = q₁, Q = ϵ and P = (a + (a(b + ab)*)b.
Therefore, according to Arden’s theorem, we can write it as:
q₁ = ϵ(a + (a(b + ab)*)b)*
= (a + (a(b + ab)*)b)* [From identity eq.: ϵR = R] - (6)
The last step is to substitute these values in the final state. The final state for the given example is q₃.
q₃ = q₂a
Substituting q2 from the equation (5):
q₃ = q₁a(b + ab)*a
Substituting q1 from the equation (6):
q₃ = (a + (a(b + ab)*)b)* a(b + ab)*a
We can see that now the equation is represented as a combination of the input symbols a and b only. Thus we have converted the given NFA to a regular expression.