Radians and Degrees | Mathematics for ACT PDF Download

Radians to degrees is a form of conversion used to convert the measurement of angles in geometry. To measure an angle, there are two different measuring systems. The two units used to measure an angle are radians and degrees. The unit radians is used mostly in the concept of trigonometry. The measure of angles can be converted from radians to degrees using a formula. To understand this formula and conversion of radians to degrees, we will understand the meaning of each unit of angle. We will also see the conversion table for radians to degrees in this article.

Radians to Degrees Conversion

There are two different units used to measure an angle: radians and degrees. Hence, it is important for us to be proficient in the conversion of units of angle, that is radians to degrees and degrees to radians. When we take the radius of a circle and revolve it, we start constructing an angle that can be measured in radians or degrees. Let us see what each unit of angle means and how to measure the angle.

Radians
When we rotate the radius completely around the circle, it completes one rotation. The angle subtended at the center of the circle by the radius after one complete rotation is 2π radians. The angle in radians subtended by the radius at the center of the circle is the ratio of the length of the arc to the length of the radius. When the length of the arc becomes equal to the length of the radius, the angle subtended at the center becomes 1 radian. We denote the unit radian as rad. Radians is the SI unit of measuring angles.

Degrees
Angles are measured in degrees. One revolution is divided into 360 equal parts and each part is called a degree. The angle subtended at the center of the circle after one complete rotation of the radius is 360°. The symbol for degrees is denoted by '°'. Degrees is not an SI unit to measure angles but it is an accepted unit to measure. Hence, while solving problems, it is preferred to convert the unit of angle from radians to degrees to understand it better. The instrument used to measure an angle in degrees is a protractor.
Comparing the measures of the angle for a complete rotation, we observe,

• 360 Degrees = 2π Radians
• 180 Degrees = π Radians

Radians to Degrees Formula

The radians to degrees formula is used to convert radians to degrees. To convert radians to degrees we need to multiply the radians by 180°/π radians. When we measure angles we use two types of units: degrees and radians, 1 degree is written as 1°. And 1 radian is written as 1 (or) 1c i.e. if there is no unit after the measure of an angle, it means that it is in radians. One rotation in a circle is divided into 360 equal parts and each part is called a degree. One complete counterclockwise rotation in radians is 2π and in degrees, it is 360°. Thus, degree measure and radian measure are related. The formula to convert an angle in radians to degrees is:
Angle in Radians × 180°/π = Angle in Degrees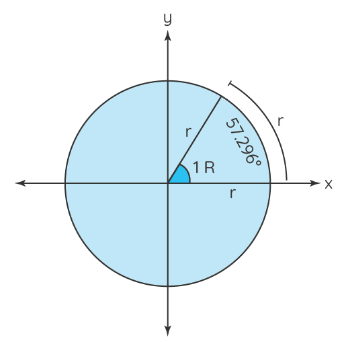

Derivation of Radians to Degrees Formula

One complete rotation around a circle gives 2π radians which is equivalent to 360°. Therefore, we have 2π radians = 360°. Now, to derive the formula for the conversion of radians to degrees, we will simplify this equation.
2π radians = 360°
π radians = 360°/2
π radians = 180°
1 radian = 180°/π
Hence the angle in degrees is obtained by multiplying the angle in radians by 180°/π. i.e.,
Angle in Radians × 180°/π = Angle in Degrees
Hence, the radians to degrees formula has been derived.

Degrees = Radians × 180°/π

Therefore, to convert radians to degrees, use this formula = Radian measure × (180°/π). The final unit of measure will be (°). 1 rad equals 57.296°.

How to Convert Radians to Degrees?

Radians and degrees are the two units to measure angles. 2π radians is equivalent to 360° that is obtained after one complete revolution of a circle. The conversion of radians to degrees can be done using the formula 'Angle in Radians × 180°/π = Angle in Degrees'. Any angle given in radians can be converted to degrees using the steps given below,

• Note down the measure of the angle given in radians.
• We know, 1 radian = 180°/π. So, to convert the angle given in radians to degrees we multiply it with 180°/π.
• Angle in Degrees = Angle in Radians × 180°/π
• Simplify the values and express the answer in degrees(°).

Let us understand this with the help of an example.
Consider an angle π / 6 radians. Now, we need to convert the radians to degrees for this angle using the formula of conversion.
(π / 6) × (180°/π) = (Angle in Degrees)
Angle in Degrees = 180°/6 = 30°
Hence, π / 6 radians is equal to 30°.

Radians to Degrees Conversion Table

Now, let us collate the conversion of specific angles from radians to degrees which are more frequently used while solving problems. The below-given table shows the radian values for the corresponding angle measures in degrees:

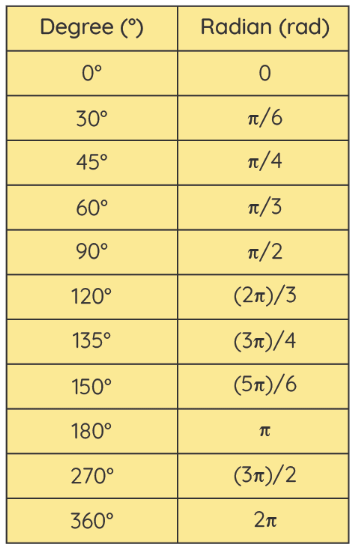
Radians to Degrees Chart

We can also refer to the following radians to degrees chart to see the measure of any angle in degrees with respect to its measure in radians. We know that for a unit circle, the circumference will be equal to 2π, which is similar to rotating 360º as shown below.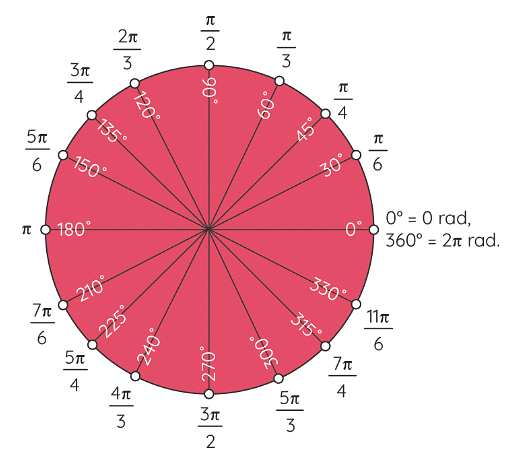

Important Notes on Radians to Degrees
Here is a list of a few important points that should be kept in mind while converting radians to degrees:

• Angles are measured using two basic units: degrees and radians.
• One complete counterclockwise revolution is equal to 2π rad in radians.
• 1° equals 0.017453 radians and 1 rad equals 57.2958°.
• To convert an angle from radians to degrees, we multiply it by 180°/π.
• To convert an angle from degrees to radians, we multiply it by π/180°.

Radians to Degrees Example

Example: Convert the angle π/5 rad into degrees using the radians to degrees formula.
Solution: The formula to convert radians to degrees is:
Angle in Radians × 180°/π = Angle in Degrees
(π/5) × (180°/π )= Angle in Degrees
Angle in degrees = 180°/5
Angle in degrees = 36°
Hence, π/5 rad is equal to 36° using the radians to degrees formula.