Number System | Digital Logic - Computer Science Engineering (CSE) PDF Download
Number System is a method of representing Numbers on the Number Line with the help of a set of Symbols and rules. These symbols range from 0-9 and are termed as digits. Number System is used to perform mathematical computations ranging from great scientific calculations to calculations like counting the number of Toys for a Kid or Number of chocolates remaining in the box. Number Systems comprise of multiple types based on the base value for its digits.
What is the Number Line?
A Number line is a representation of Numbers with a fixed interval in between on a straight line. A Number line contains all the types of numbers like natural numbers, rationals, Integers, etc. Numbers on the number line increase while moving from Left to Right and decrease while moving from right to left. The ends of a number line are not defined i.e., numbers on a number line range from infinity on the left side of the zero to infinity on the right side of the zero.
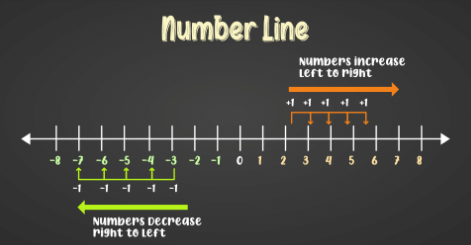
- Positive Numbers: Numbers that are represented on the right side of the zero are termed as Positive Numbers. The value of these numbers increases on moving towards the right. Positive numbers are used for Addition between numbers. Example: 1, 2, 3, 4, …
- Negative Numbers: Numbers that are represented on the left side of the zero are termed as Negative Numbers. The value of these numbers decreases on moving towards the left. Negative numbers are used for Subtraction between numbers. Example: -1, -2, -3, -4, …
Number and Its Types
A number is a value created by the combination of digits with the help of certain rules. These numbers are used to represent arithmetical quantities. A digit is a symbol from a set 10 symbols ranging from 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Any combination of digits represents a Number. The size of a Number depends on the count of digits that are used for its creation.
For Example: 123, 124, 0.345, -16, 73, 9, etc.
Types of Numbers
Numbers are of various types depending upon the patterns of digits that are used for their creation. Various symbols and rules are also applied on Numbers which classifies them into a variety of different types:

- Natural Numbers: Natural Numbers are the most basic type of Numbers that range from 1 to infinity. These numbers are also called Positive Numbers or Counting Numbers. Natural Numbers are represented by the symbol N.
- Example: 1, 2, 3, 4, 5, 6, 7, and so on.
- Whole Numbers: Whole Numbers are basically the Natural Numbers, but they also include ‘zero’. Whole numbers are represented by the symbol W.
- Example: 0, 1, 2, 3, 4, and so on.
- Integers: Integers are the collection of Whole Numbers plus the negative values of the Natural Numbers. Integers do not include fraction numbers i.e. they can’t be written in a/b form. The range of Integers is from the Infinity at the Negative end and Infinity at the Positive end, including zero. Integers are represented by the symbol Z.
- Example: ...,-4, -3, -2, -1, 0, 1, 2, 3, 4,...
- Fractions: Fractions are the numbers that are written in the form of a/b, where, a belongs to Whole numbers and b belongs to Natural Numbers, i.e., b can never be 0. The upper part of the fraction i.e. a is termed as a Numerator whereas the lower part i.e. b is called Denominator.
- Example: 1/2, 3/7, 8/3, etc.
- Rational Numbers: Rational numbers are the numbers that can be represented in the fraction form i.e. a/b. Here, a and b both are integers and b≠0. All the fractions are rational numbers but not all the rational numbers are fractions.
- Example: -2/5, 0.54, 1/5, 13/4, ...
- Irrational Numbers: Irrational numbers are the numbers that can’t be represented in the form of fractions i.e. they can not be written as a/b.
- Example: √2, √3, √.434343, π...
- Real and Imaginary Numbers: Real numbers are the numbers that can be represented in the decimal form. These numbers include whole numbers, integers, fractions, etc. All the integers belong to Real numbers but all the real numbers do not belong to the integers.
Imaginary Numbers are all those numbers that are not real numbers. These numbers when squared will result in a negative number. The √-1 is represented as i. These numbers are also called complex numbers.- Example: √-2, √-5,...
- Prime Numbers and Composite Numbers: Numbers that do not have any factors other than 1 and the number itself are termed as Prime Numbers. All the numbers other than Prime Numbers are termed as Composite Numbers except 0. Zero is neither prime nor a composite number.
- Example: 2, 3, 5, 7,... are prime numbers and 4, 6, 8, 9, 12,... are composite numbers
Types of Number Systems
Based on the base value and the number of allowed digits, number systems are of many types. The four common types of Number System are:
- Decimal Number System
- Binary Number System
- Octal Number System
- Hexadecimal Number System

Decimal Number System
Number system with a base value 10 is termed as Decimal number system. It uses 10 digits i.e. 0-9 for the creation of numbers. Here, each digit in the number is at a specific place with place value a product of different powers of 10. Here, the place value is termed from right to left as first place value called units, second to the left as Tens, so on Hundreds, Thousands, etc. Here, units have a place value as 100, tens have a place value as 101, hundreds as 102, thousands as 103, and so on.
Example: 10285 has place values as
(1 × 104) + (0 × 103) + (2 × 102) + (8 × 101) + (5 × 100)
1 × 10000 + 0 × 1000 + 2 × 100 + 8 × 10 + 5 × 1
10000 + 0 + 200 + 80 + 5
10285
Binary Number System
Number System with a base value 2 is termed as Binary number system. It uses 2 digits i.e. 0 and 1 for the creation of numbers. The numbers formed using these two digits are termed as Binary Numbers. Binary number system is very useful in electronic devices and computer systems because it can be easily performed using just two states ON and OFF i.e. 0 and 1.
Decimal Numbers 0-9 are represented in binary as: 0, 1, 10, 11, 100, 101, 110, 111, 1000, and 1001.
Examples:
14 can be written as 1110
19 can be written as 10011
50 can be written as 110010
Octal Number System
Octal Number System is one in which the base value is 8. It uses 8 digits i.e. 0-7 for creation of Octal Numbers. Octal Numbers can be converted to Decimal value by multiplying each digit with the place value and then adding the result. Here the place values are 80, 81, and 82. Octal Numbers are useful for the representation of UTF8 Numbers.
Example:
(135)10 can be written as (207)8
(215)10 can be written as (327)8
Hexadecimal Number System
Number System with base value 16 is termed as Hexadecimal Number System. It uses 16 digits for the creation of its numbers. Digits from 0-9 are taken like the digits in the decimal number system but the digits from 10-15 are represented as A-F i.e. 10 is represented as A, 11 as B, 12 as C, 13 as D, 14 as E, and 15 as F. Hexadecimal Numbers are useful for handling memory address locations.
Examples:
(255)10 can be written as (FF)16
(1096)10 can be written as (448)16
(4090)10 can be written as (FFA)16
Conversion of Number Systems
Conversion between numbers systems is quite an easy task. Any number from any number system can be converted to other number systems with the help of certain methods that will be discussed below:
Conversion from Decimal Number System to Other Number Systems
Decimal Numbers are represented with digits 0-9 and with base 10. Conversion of a number system means conversion from one base to another. Following are the conversion of the Decimal Number System to other Number Systems:
Decimal to Binary Conversion:
Decimal numbers are represented in base 10, but the binary numbers are of base 2. Hence, to convert a decimal number to binary number, the base of that number is to be changed. Follow the steps given below:
- Step 1: Divide the Decimal Number with the base of the number system to be converted to. Here the conversion is to binary, hence the divisor will be 2.
- Step 2: The remainder obtained from the division will become the least significant digit of the new number.
- Step 3: The quotient obtained from the division will become the next dividend and will be divided by base i.e. 2.
- Step 4: The remainder obtained will become the second least significant digit i.e. it will be added in the left of the previously obtained digit.
Now, the steps 3 and 4 are repeated until the quotient obtained becomes 0, and the remainders obtained after each iteration are added to the left of the existing digits.
After all the iterations are over, the last obtained remainder will be termed as the Most Significant digit.
Decimal to Octal Conversion:
Octal Numbers are represented in base 8. Hence, to convert a decimal number to octal number, the base of that number is to be changed. Follow the steps given below:
- Step 1: Divide the Decimal Number with the base of the number system to be converted to. Here the conversion is to octal, hence the divisor will be 8.
- Step 2: The remainder obtained from the division will become the least significant digit of the new number.
- Step 3: The quotient obtained from the division will become the next dividend and will be divided by base i.e. 8.
- Step 4: The remainder obtained will become the second least significant digit i.e. it will be added in the left of the previously obtained digit.
Now, the steps 3 and 4 are repeated until the quotient obtained becomes 0, and the remainder obtained after each iteration are added to the left of the existing digits.

Decimal to Hexadecimal Conversion:
Hexadecimal Numbers are represented in base 16. Hence, to convert a decimal number to hexadecimal number, the base of that number is to be changed. Follow the steps given below:
- Step 1: Divide the Decimal Number with the base of the number system to be converted to. Here the conversion is to Hex hence the divisor will be 16.
- Step 2: The remainder obtained from the division will become the least significant digit of the new number.
- Step 3: The quotient obtained from the division will become the next dividend and will be divided by base i.e. 16.
- Step 4: The remainder obtained will become the second least significant digit i.e. it will be added in the left of the previously obtained digit.
Now, the steps 3 and 4 are repeated until the quotient obtained becomes 0, and the remainder obtained after each iteration are added to the left of the existing digits.
Conversion from Binary Number System to Other Number Systems
Binary Numbers are represented with digits 0 and 1 and with base 2. Conversion of a number system means conversion from one base to another. Following are the conversion of the Binary Number System to other Number Systems:
Binary to Decimal Conversion:
Binary numbers are represented in base 2 but the decimal numbers are of base 10. Hence, to convert the binary number into a decimal number, the base of that number is to be changed. Follow the steps given below:
- Step 1: Multiply each digit of the Binary number with the place value of that digit, starting from right to left i.e. from LSB to MSB.
- Step 2: Add the result of this multiplication and the decimal number will be formed.
Example: To convert (11101011)2 into a decimal number
Binary to Octal Conversion:
Binary numbers are represented in base 2 but the octal numbers are of base 8. Hence, to convert the binary number into octal number, the base of that number is to be changed. Follow the steps given below:
- Step 1: Divide the binary number into groups of three digits starting from right to left i.e. from LSB to MSB.
- Step 2: Convert these groups into equivalent octal digits.
Example: To convert (11101011)2 into an octal number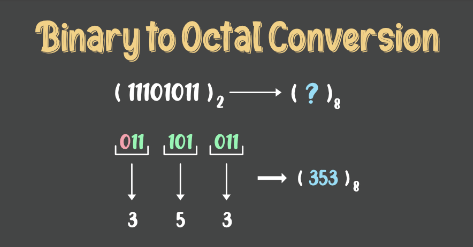
Binary to Hexadecimal Conversion:
Binary numbers are represented in base 2 but the Hexadecimal numbers are of base 10. Hence, to convert the binary number into Hex number, the base of that number is to be changed. Follow the steps given below:
- Step 1: Divide the binary number into groups of four digits starting from right to left i.e. from LSB to MSB.
- Step 2: Convert these groups into equivalent hex digits.
Example: To convert (1110101101101)2 into a hex number

Conversion from Octal Number System to Other Number Systems
Octal Numbers are represented with digits 0-7 and with base 8. Conversion of a number system means conversion from one base to another. Following are the conversions of the Octal Number System to other Number Systems:
Octal to Decimal Conversion:
Octal numbers are represented in base 8, but the decimal numbers are of base 10. Hence, to convert an octal number to a decimal number, the base of that number is to be changed. Follow the steps given below:
- Step 1: Multiply each digit of the Octal number with the place value of that digit, starting from right to left i.e. from LSB to MSB.
- Step 2: Add the result of this multiplication and the decimal number will be formed.
Example:

Octal to Binary Conversion:
Octal numbers are represented in base 8, but the binary numbers are of base 2. Hence, to convert an octal number to a binary number, the base of that number is to be changed. Follow the steps given below:
- Step 1: Write each digit of the octal number separately.
- Step 2: Convert each digit into an equivalent group of three binary digits.
- Step 3: Combine these groups to form the whole binary number.
Example: (247)8 is to be converted to binary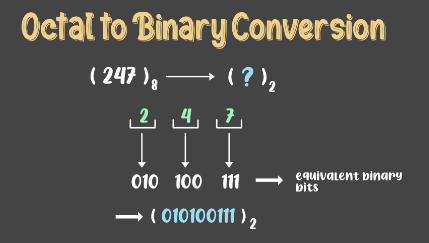
Octal to Hexadecimal Conversion:
Octal numbers are represented in base 8, but the hexadecimal numbers are of base 16. Hence, to convert an octal number to a hex number, the base of that number is to be changed. Follow the steps given below:
- Step 1: We need to convert the Octal number to Binary first. For that, follow the steps given in the above conversion.
- Step 2: Now to convert the binary number to Hex number, divide the binary digits into groups of four digits starting from right to left i.e. from LSB to MSB.
- Step 3: Add zeros prior to MSB to make it a proper group of four digits(if required)
- Step 4: Now convert these groups into their relevant decimal values.
- Step 5: For values from 10-15, convert it into Hex symbols i.e from A-F
Example: (5456)8 is to be converted to hex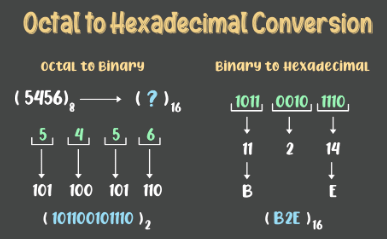
Conversion from Hexadecimal Number System to Other Number Systems
Hex Numbers are represented with digits 0-9 and with letters A-F and with base 16. Conversion of a number system means conversion from one base to another. Following are the conversions of the Hexadecimal Number System to other Number Systems:
Hexadecimal to Decimal Conversion:
Hexadecimal numbers are represented in base 16 but the decimal numbers are of base 10. Hence, to convert a hexadecimal number to a decimal number, the base of that number is to be changed. Follow the steps given below:
- Step 1: Write the decimal values of the symbols used in the Hex number i.e. from A-F
- Step 2: Multiply each digit of the Hex number with its place value. starting from right to left i.e. LSB to MSB.
- Step 3: Add the result of multiplications and the final sum will be the decimal number.
Example: To convert (8EB4)16 into a decimal value
Hexadecimal to Binary Conversion:
Hex numbers are represented in base 16, but the binary numbers are of base 2. Hence, to convert a hexadecimal number to a binary number, the base of that number is to be changed. Follow the steps given below:
- Step 1: Convert the Hex symbols into its equivalent decimal values.
- Step 2: Write each digit of the Hexadecimal number separately.
- Step 3: Convert each digit into an equivalent group of four binary digits.
- Step 4: Combine these groups to form the whole binary number.
Example: (B2E)16 is to be converted to binary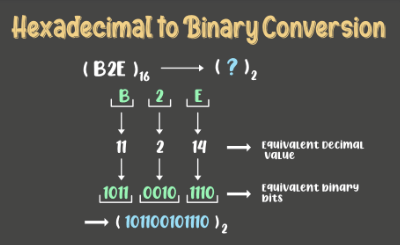
Hexadecimal to Octal Conversion:
Hexadecimal numbers are represented in base 16, but the octal numbers are of base 8. Hence, to convert a hex number to an octal number, the base of that number is to be changed. Follow the steps given below:
- Step 1: We need to convert the Hexadecimal number to Binary first. For that, follow the steps given in the above conversion.
- Step 2: Now to convert the binary number to Octal number, divide the binary digits into groups of three digits starting from right to left i.e. from LSB to MSB.
- Step 3: Add zeros prior to MSB to make it a proper group of three digits(if required)
- Step 4: Now convert these groups into their relevant decimal values.
Example: (B2E)16 is to be converted to hex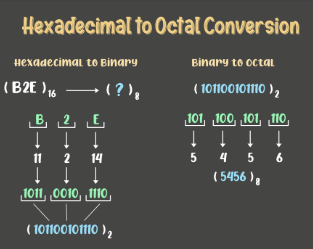
|
50 docs|15 tests
|
















