Functional Completeness in Digital Logic | Digital Logic - Computer Science Engineering (CSE) PDF Download

Clear all your Computer Science Engineering (CSE) doubts with EduRev Join for Free

Join for Free

A set of operations is said to be functionally complete or universal if and only if every switching function can be expressed by means of operations in it. A set of Boolean functions is functionally complete, if all other Boolean functions can be constructed from this set and a set of input variables are provided, e.g.

• Set A = {+,*,’ (OR, AND, complement) } are functionally complete.
• Set B = {+,’} are functionally complete
• Set C = {*,’} are functionally complete

Post’s Functional Completeness Theorem – Important closed classes of functions:

• T₀ – class of all 0-preserving functions, such as f(0, 0, … , 0) = 0.
• T₁ – class of all 1-preserving functions, such as f(1, 1, … , 1) = 1.
• S – class of self-dual functions, such as f(x₁, … ,x_n) = ¬ f(¬x₁, … , ¬x_n).
• M – class of monotonic functions, such as : {x₁, … ,x_n} ≤ {x₁, … ,x_n}, if x_i ≤ y_i
  if {x₁, … ,x_n} ≤ {x₁, … ,x_n}
  then f(x₁, … ,x_n) ≤ f(x₁, … ,x_n)
• L – class of linear functions, which can be presented as: f(x₁, … ,x_n) = a₀ + a₁·x₁ + … + a_n·x_n ; ai {0, 1}.

Theorem– A system of Boolean functions is functionally complete if and only if for each of the five defined classes T₀, T₁, S, M, L, there is a member of F which does not belong to that class.
These are minimal functionally complete operator sets –

• One element –
  {↑}, {↓}.
• Two elements –
  
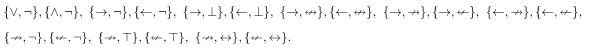
• Three elements –
  

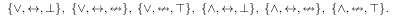
Examples on functional Completeness 

• Check if function F(A,B,C) = A’+BC’ is functionally complete?
• Explanation – Let us start by putting all variables as ‘A’ so it becomes
  F(A,A,A) = A’+A.A’ = A’ ...(i)
  F(B,B,B) = B’+B.B’ = B’ ...(ii)
  Now substitute F(A,A,A) in place of variable ‘A’ and F(B,B,B) in place of variable ‘C’
  F(F(A,A,A),B,F(B,B,B)) = (A’)’+B.(B’)’ = A+B ...(iii)
  from (i) and (ii) complement is derived and from (iii) operator ‘+’ is derived so this function is functionally complete as from above if function contains {+,’} is functionally complete.
• Check if function F(A,B) = A’+B is functionally complete?
• Explanation – Let us start by putting all variables as ‘A’ so it becomes
  F(A,A) = A’+A = 1 ...(i)
  F(B,B) = B’+B = 1 ...(ii)
  F(A,0) = A’+0 = A’ ...(iv)
  Now substitute F(A,0) in place of variable ‘A’
  F(F(A,0),B) = (A’)’+B = A+B ...(iii)
  from (iv) complement is derived and from (iii) operator ‘+’ is derived so this function is functionally complete as from above if function contains {+,’} is partially functionally complete.
• Check if function F(A, B) = A’B is functionally complete?
• Explanation – Let us start by putting all variables as ‘A’ so it becomes
  F(A,A) = A’.A’ = 0 ...(i)
  F(A,0) = A’.0 = 0 ...(ii)
  F(A,1) = A’.1 = A’ ...(iv)
  Now substitute F(A,1) in place of variable ‘A’
  F(F(A, 1),B) = (A’)’*B = A*B ...(iii)
  from (iv) complement is derived and from (iii) operator ‘*’ is derived so this function is functionally complete as from above if function contains {*,’} is partially functionally complete .
  Note – If the function becomes functionally complete by substituting ‘0’ or ‘1’ then it is known as partially functionally complete.
• Check if function F(A,B) = A’B+AB’ (EX-OR) is functionally complete?
• Explanation – Let us start by putting all variables as ‘A’ so it becomes
  F(A,1) = A’.1 + A.0 = A’ ...(i)
  F(A’,B) = AB + A’B’ ...(ii)
  F(A’,B’) = AB’ + A’B ...(iii)
  F(A,B’) = A’B’ + AB ...(iv)
  So there is no way to get {+,*,’} according to condition. So EX-OR is non functionally complete.
• Consider the operations
  f(X, Y, Z) = X’YZ + XY’ + Y’Z’ and g(X′, Y, Z) = X′YZ + X′YZ′ + XY