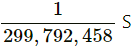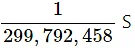HC Verma Questions and Solutions: Chapter 1- Introduction to Physics- 2 | HC Verma Solutions - JEE PDF Download
Short Answers
Q1. The metre is defined as the distance travelled by light in  second. Why didn't people choose some easier number such as
second. Why didn't people choose some easier number such as  second? Why not 1 second?
second? Why not 1 second?
The speed of light in vacuum is 299,792,458 m/s.
Then time taken by light to cover a distance of 1 metre in vacuum =
Hence, the metre is defined as the distance travelled by light in
As 300,000,000 m/s is an approximate speed of light in vacuum, it cannot be used to define the metre.
The distance travelled by light in one second is 299,792,458 m. This is a large quantity and cannot be used as a base unit. So, the metre is not defined in terms of second.
Q2.1. What are the dimensions of volume of a cube of edge a.
Volume of a cube of edge a, V = a × a × a
i.e [ V ] = L × L × L = L3
Q2.2. What are the dimensions of volume of a sphere of radius a?
Volume of a sphere of radius a, V = 4/3π(a)3
i.e [ V ] = L × L × L = L3
Q2.3. What are the dimensions of the ratio of the volume of a cube of edge a to the volume of a sphere of radius a?
The ratio of the volume of the cube to the volume of the sphere is a dimensionless quantity.
- The volume of a cube is calculated using the formula: Vcube = a3.
- The volume of a sphere is calculated using the formula: Vsphere = (4/3)πa3.
Thus, the ratio can be expressed as:
- Ratio = Vcube / Vsphere = a3 / ((4/3)πa3)
- After simplification, this results in a dimensionless number.
Q3. Suppose you are told that the linear size of everything in the universe has been doubled overnight. Can you test this statement by measuring sizes with a metre stick? Can you test it by using the fact that the speed of light is a universal constant and has not changed? What will happen if all the clocks in the universe also start running at half the speed?
The validity of this statement cannot be tested by measuring sizes with a metre stick, because the size of the metre stick has also doubled overnight. Additionally, the statement cannot be verified using the fact that the speed of light is a universal constant and has not changed, as everything, including light, would also be affected by the doubling of size. If all the clocks in the universe started running at half the speed, it would lead to a situation where time itself would appear to run slower. Consequently, events would unfold in a way that is still consistent with the laws of physics, but our perception of time would be altered.
Q4. If all the terms in an equation have the same units, is it necessary that they have the same dimensions? If all the terms in an equation have the same dimensions, is it necessary that they have the same units? Yes, if all the terms in an equation have the same units, it is necessary that they have the same dimension.
No, if all the terms in an equation have the same dimensions, it is not necessary that they have the same unit. It is because two quantities with different units can have the same dimension, but two quantities with different dimensions cannot have the same unit. For example angular frequency and frequency, both have the dimensions [T-1] but units of angular frequency is rad/s and frequency is Hertz.Another example is energy per unit volume and pressure. Both have the dimensions of [ML-1T-2] but units of pressure is N/m2 and that of energy per unit volume is J/m3.
Q5. If two quantities have same dimensions, do they represent same physical content?
No, even if two quantities have the same dimensions, they may represent different physical contents.
Example: Torque and energy have the same dimension, but they represent different physical contents.
Q6. It is desirable that the standards of units be easily available, invariable, indestructible and easily reproducible. If we use foot of a person as a standard unit of length, which of the above features are present and which are not?
If we use the foot of a person as a standard unit of length, the following features will be affected:
Features that will not be present:Feature that will be present:
- Variability – The foot size can differ from person to person.
- Destructibility – The measurement may not withstand certain conditions.
- Reproducibility – It is difficult to reproduce an exact foot measurement consistently.
- Availability – The foot of a person can be easily used to measure length.
Q7.1. Suggest a way to measure the thickness of a sheet of paper.
The thickness of a sheet of paper can roughly be determined by measuring the height of a stack of paper.
Example: Let us consider a stack of 100 sheets of paper. We will use a ruler to measure its height. In order to determine the thickness of a sheet of paper, we will divide the height of the stack with the number of sheets (i.e., 100).
Q7.2. Suggest a way to measure the distance between the sun and the moon.
The distance between the Sun and the Moon can be measured by using Pythagoras theorem when the Earth makes an angle of 90∘ with the Sun and the Moon. We already know the distances from the Sun to the Earth and from the Earth to the Moon. However, these distances keep on changing due to the revolution of the Moon around the Earth and the revolution of the Earth around the Sun.
|
134 docs
|
FAQs on HC Verma Questions and Solutions: Chapter 1- Introduction to Physics- 2 - HC Verma Solutions - JEE
| 1. What is the importance of studying physics? |  |
| 2. How can I improve my understanding of physics concepts? |  |
| 3. What are the basic principles of physics? |  |
| 4. How can I excel in physics exams? |  |
| 5. What are some common misconceptions about physics? |  |