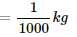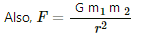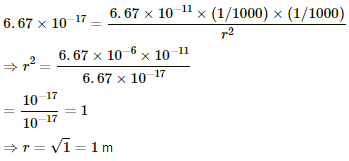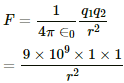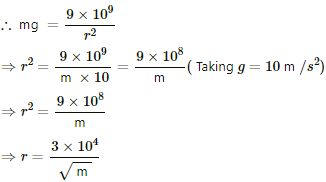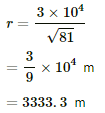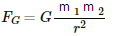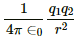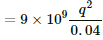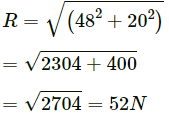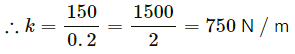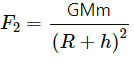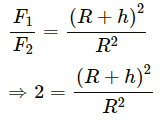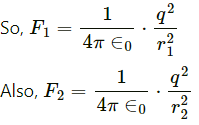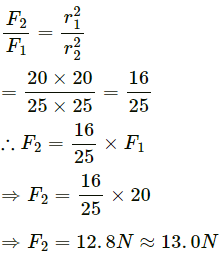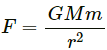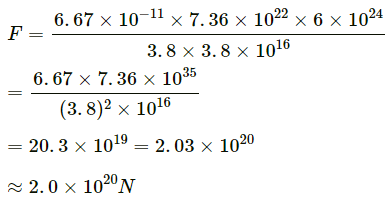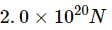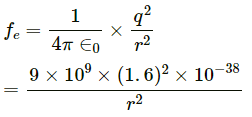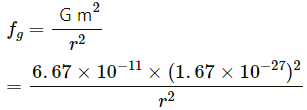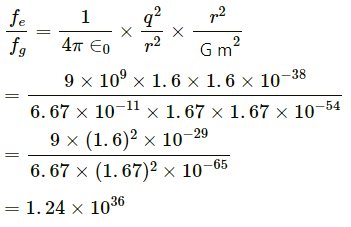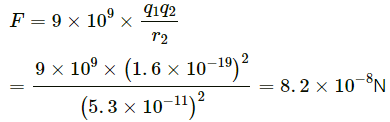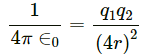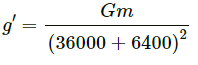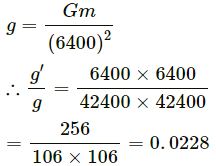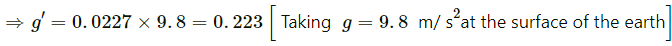HC Verma Questions and Solutions: Chapter 4- The Forces- 2 | HC Verma Solutions - JEE PDF Download
Exercise
Q.1. The gravitational force acting on a particle of 1 g due to a similar particle is equal to 6.67 × 10−17 N. Calculate the separation between the particles.
Mass of the particle, m = 1 gm =
Let the distance between the two particles be r.
Gravitational force between the particle, F = 6.67 × 10−17 N
Substituting the respective values in the above formula, we get :
∴ The separation between the particles is 1 m.
Q.2. Calculate the force with which you attract the earth.
Consider that a man is standing on the surface of the Earth.
Force acting on the man = mg
Here, m = mass of the man and g = acceleration due to gravity on the surface of earth (=10 m/s2)
Assume that the mass of the man is equal to 65 kg.
Then F = W = mg = 65 × 10 = 650 N = force acting on the man
∴ By Newton's third law (action-reaction are always equal), the man is also attracting the earth with a force of 650 N in the opposite direction.
Q.3. At what distance should two charges, each equal to 1 C, be placed so that the force between them equals your weight?
Given : q1 = q2 = 1C
By Coulomb's law, the force of attraction between the two charges is given by
However, the force of attraction is equal to the weight (F = mg).
Assuming that m = 81 kg, we have :
∴ The distance r is 3333.3 m.
Q.4. Two spherical bodies, each of mass 50 kg, are placed at a separation of 20 cm. Equal charges are placed on the bodies and it is found that the force of Coulomb repulsion equals the gravitational attraction in magnitude. Find the magnitude of the charge placed on either body.
Mass = 50 kg
Separation between the masses, r = 20 cm = 0.2 m
Let the change on each sphere be q.
Now, gravitational force,
Coulomb force F_c =
Since FG = Fc, we have :
Thus, the charge of the spherical body is 4.3 x 10-9 C
Q.5. A monkey is sitting on a tree limb. The limb exerts a normal force of 48 N and a frictional force of 20 N. Find the magnitude of the total force exerted by the limb on the monkey.
Given: The limb of the tree exerts a normal force of 48 N and a frictional force of 20 N.
So, resultant magnitude of the force if given by
∴ The magnitude of the total force exerted by the limb on the monkey is 52 N.
Q.6. A body builder exerts a force of 150 N against a bullworker and compresses it by 20 cm. Calculate the spring constant of the spring in the bullworker.
Force exerted by the body builder against the bullworker = 150 N
Compression in the bullworker, x = 20 cm = 0.2 m
∴ Total force exerted, f = kx = 150
Here, k is the spring constant of the spring in the bullworker.
Hence, the spring constant of the spring in the bullworker is 750 N/m.
Q.7. A satellite is projected vertically upwards from an earth station. At what height above the earth's surface will the force on the satellite due to the earth be reduced to half its value at the earth station? (Radius of the earth is 6400 km.)
Let h be the height, M be the Earth's mass, R be the Earth's radius and m be the satellite's mass .
Force on the satellite due to the earth when it is at the Earth's surface, F1 = GMm/R2
Force on the satellite due to the earth when it is at height h above the Earth's surface,
According to question, we have :
Taking square root on both sides, we get: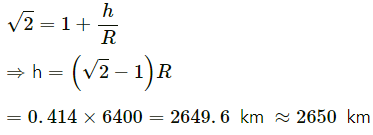
Q.8. Two charged particles placed at a separation of 20 cm exert 20 N of Coulomb force on each other. What will be the force of the separation is increased to 25 cm?
Two charged particles placed at a separation of 20 cm exert 20 N of Coulomb force on each other.
According to the question, we have :
Therefore, the two charged particles will exert a force of 13.0 N on each other, if the separation is increased to 25 cm.
Q.9. The force with which the earth attracts an object is called the weight of the object. Calculate the weight of the moon from the following data : The universal constant of gravitation G = 6.67 × 11−11 N−m2/kg2, mass of the moon = 7.36 × 1022 kg, mass of the earth = 6 × 1024 kg and the distance between the earth and the moon = 3.8 × 105 km.
The force between the Earth and the Moon is given by
Here, M is the mass of the earth; m is the mass of the moon and r is the distance between Earth and Moon.
On substituting the values, we get :
∴ The weight of the moon is
Q.10. Find the ratio of the magnitude of the electric force to the gravitational force acting between two protons.
Charge of the proton, q = 1.6 x 10-19 C
Mass of the proton = 1.67 x 10-27kg
Let the distance between two protons be r.
Coulomb force (electric force) between the protons is given by
Gravitational force between the protons is given by
On dividing, fe by fg, We get:
Q.11. The average separation between the proton and the electron in a hydrogen atom in ground state is 5.3 × 10−11 m. (a) Calculate the Coulomb force between them at this separation. (b) When the atom goes into its first excited state the average separation between the proton and the electron increases to four times its value in the ground state. What is the Coulomb force in this state?
Average separation between the proton and the electron of a Hydrogen atom in ground state, r = 5.3 × 10−11 m
(a) Coulomb force when the proton and the electron in a hydrogen atom in ground state
(b) Coulomb force when the average distance between the proton and the electron becomes 4 times that of its ground state
Coulomb force, F =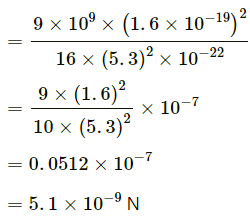
Q.12. The geostationary orbit of the earth is at a distance of about 36000 km from the earth's surface. Find the weight of a 120-kg equipment placed in a geostationary satellite. The radius of the earth is 6400 km.
The geostationary orbit of the Earth is at a distance of about 36000 km. We know that the value acceleration due to gravity above the surface of the Earth is given by
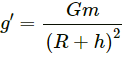
At h = 36000 km, we have :
At the surface, we have :
For a 120 kg equipment placed in a geostationary satellite, its weight will be mg' = 120 × 0.233
⇒ 26.76 ≈ 27 N
|
134 docs
|
FAQs on HC Verma Questions and Solutions: Chapter 4- The Forces- 2 - HC Verma Solutions - JEE
| 1. What are the different types of forces discussed in HC Verma Solutions Chapter 4? |  |
| 2. How can we calculate the net force acting on an object? |  |
| 3. What is the difference between mass and weight? |  |
| 4. How does the force of friction affect the motion of an object? |  |
| 5. What is the significance of Newton's third law of motion? |  |