Line graphs for Time Series Data | Mathematics for Grade 10 PDF Download
What is a time series graph?
- A time series graph is a line graph that shows data such as measurements, sales or frequencies over a given time period. They can be used to show a pattern or trend in the data and are useful for making predictions about the future such as weather forecasting or financial growth.
- To draw a time series graph, we need a set of axes.
- The horizontal axis always shows the time period, and the vertical axis represents the variable being recorded against time.
For example,
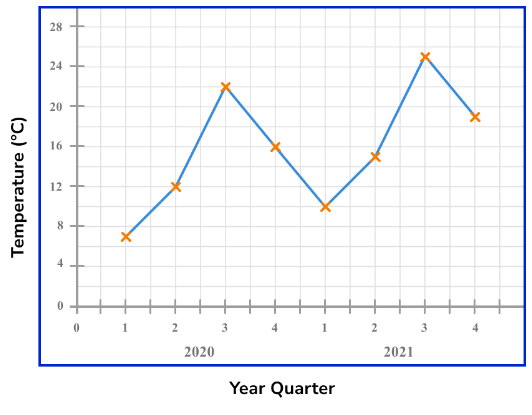
This time series graph shows the temperature of a town recorded over two years at three-monthly periods known as quarters.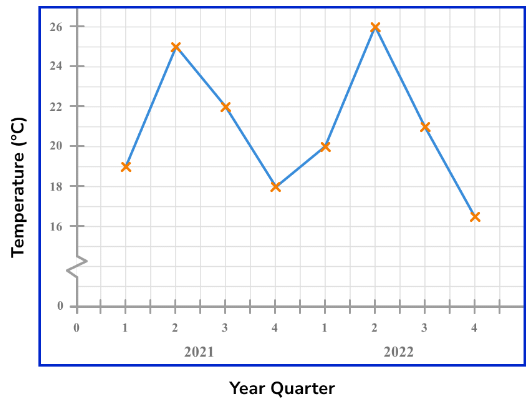
The coordinates are plotted and then joined together with straight line segments. It is important that the axis labels are clear so that the time series graph can be interpreted. The horizontal axis is always a continuous scale and both axes should increase in equal steps.
A trendline is difficult to plot for a time series when the data is clearly fluctuating (rising and falling values over time). This type of data can be described as seasonal. Instead of plotting a line of best fit, we plot a moving average.
How to draw a time series graph
In order to draw a time series graph:
- Draw and label a horizontal scale based on the time intervals of the data provided.
- Draw and label the vertical axis, choosing an appropriate scale.
- Plot the points and join with straight line segments.
Time Series Graph Examples
Example 1: Drawing a time series graph (year and quarters)
The table shows the average temperature in ºC of a city recorded for each quarter for the years 2020 and 2021.
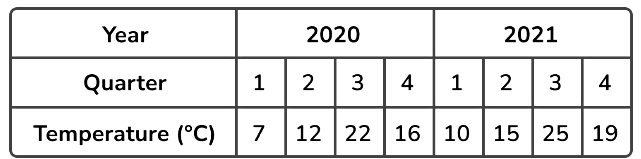
Draw a time series graph to show this data.
(i) Draw and label a horizontal scale based on the time intervals of the data provided.
The horizontal scale needs to show the eight quarters of the years 2020 and 2021.
(ii) Draw and label the vertical axis, choosing an appropriate scale.
The lowest value is ºC and the highest is 25ºC. Starting from zero will be appropriate for this data.
(iii) Plot the points and join with straight line segments.
As we know the value for each quarter and this is not grouped data, we plot the value in line with each quarter mark on the horizontal axis.
Example 2: drawing a time series graph with a break in the vertical axis
The table shows the percentage attendance of a group at a dance school over the period of a year. Draw a time series graph to show this data.
Draw a time series graph to show this data.
(i) Draw and label a horizontal scale based on the time intervals of the data provided.
The horizontal scale needs to show the twelve months of the year.
(ii) Draw and label the vertical axis, choosing an appropriate scale.
The lowest value is 37ºC and the highest is 90ºC. So for the vertical axis, we can use a break, start at 30ºC and continue in equal steps of 10 up to 100ºC.
(iii) Plot the points and join with straight line segments.
Plot each point on the exact value for each item of data.
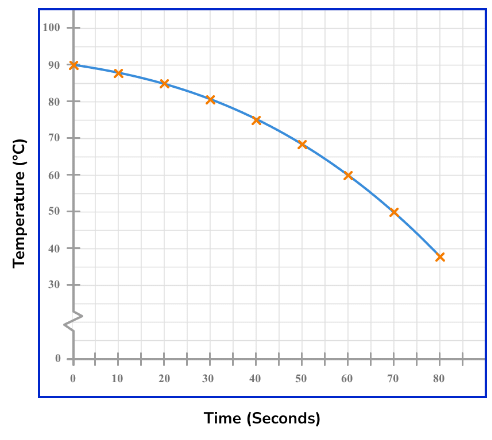
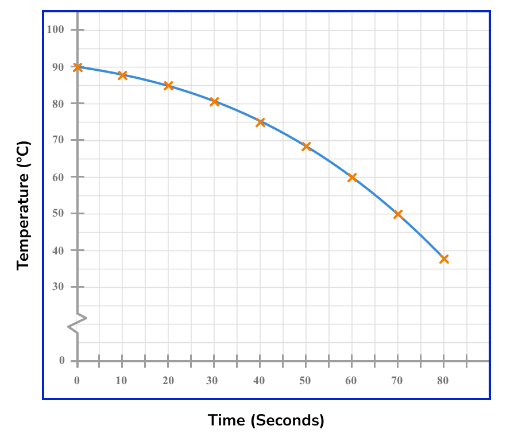
Example 3: Continuous numerical horizontal axis
The table shows the temperature, in ºC, of a hot drink, recorded every 10 seconds over a period of 80 seconds. Draw a time series graph to show this data.
Draw a time series graph to show this data.
(i) Draw and label a horizontal scale based on the time intervals of the data provided.
The range of values for the recorded times is 0 to 80. A suitable increase would be in steps of 10 for the horizontal axis.
(ii) Draw and label the vertical axis, choosing an appropriate scale.
The lowest value is 37ºC and the highest is 90ºC. So for the vertical axis, we can use a break, start at 30ºC and continue in equal steps of 10 up to 100ºC.
(iii) Plot the points and join with straight line segments.
Plot each point on the exact value for each item of data.
Interpreting a Time Series Graph
- A line of best fit is required when analysing a trend in a time series or to estimate future values. If a time series shows seasonal data (seasonality), it is far more accurate to draw a moving average than a line of best fit.
- However, a line of best fit is a quick way to be able to estimate values both within the data range (interpolation) and beyond the data range (extrapolation). This is exactly the same process for scatter graphs although the analysis is subtly different.
- We cannot use correlation descriptors for data represented in a time series plot as we are not comparing two variables, we are tracking one variable over a period of time.
Drawing a line of Best fit
- To draw a line of best fit, draw a straight line through as many points as possible, making sure that the number of data points on either side of the line of best fit is the same. Extend the line of best fit beyond the data range if required.
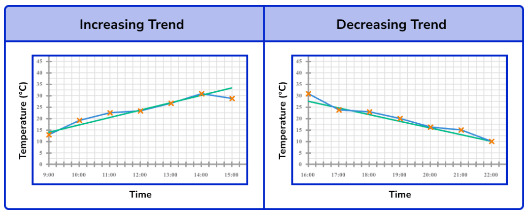
- If the line of best fit has a positive gradient, this shows that the recorded values have a positive trend (trending upwards).
- If the line of best fit has a negative gradient, this shows that the recorded values have a negative trend (trending downwards).
For example,
If we look at temperature change over time, an increasing trend would mean the temperature is increasing over time; a decreasing trend would mean the temperature is decreasing over time.
 To find a specific value within the data, we need to use the line of best fit to locate the value from the opposing axis.
To find a specific value within the data, we need to use the line of best fit to locate the value from the opposing axis.
If we know the time of the data value, we draw a vertical line up to the line of best fit, and then a horizontal line to the other axis and read the value that it reaches.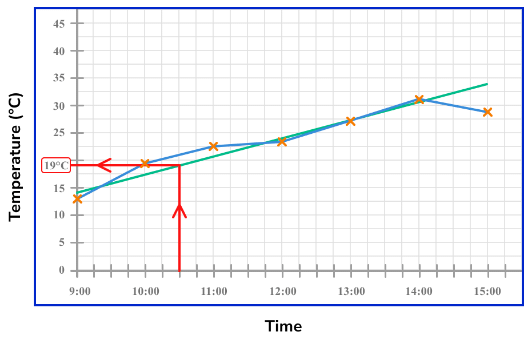
If we know the value on the vertical axis, we draw a horizontal line to the line of best fit, and then a vertical line down to the horizontal axis and read the time for that data value.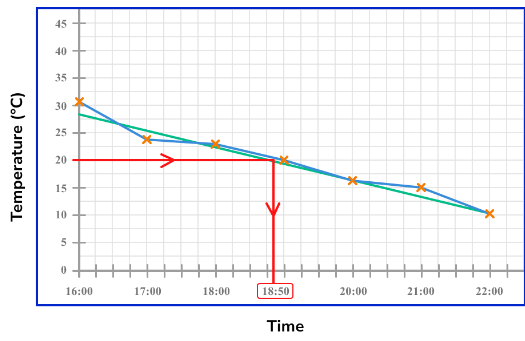 This is the same approach if the value is beyond the current data set. Here, we just need to extend the line of best fit in the same direction beyond the data and locate the required value using the method above.
This is the same approach if the value is beyond the current data set. Here, we just need to extend the line of best fit in the same direction beyond the data and locate the required value using the method above.
Note: Any value that is interpreted using the line of best fit but which is beyond the data range, is always an estimate (or prediction) as we do not know what happens to the data beyond the known values.
How to Interpret a Time Series Graph
In order to interpret a time series:
- Draw a line of best fit.
- Answer the question specifics.
Interpreting time series graphs examples
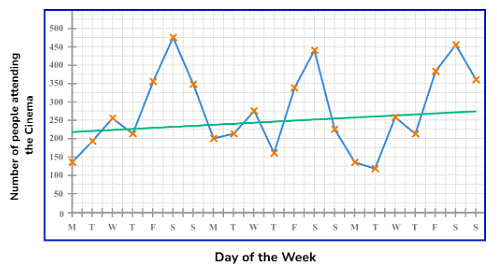
Example 1: Describe the trend in the data
Below is a time series showing the number of people attending the cinema over a three week period.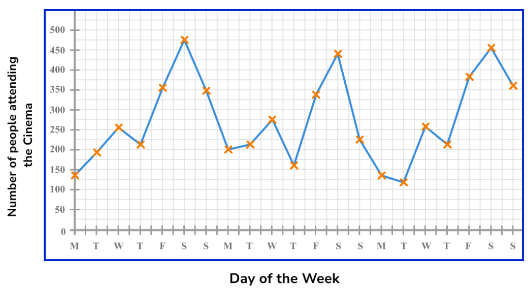 Describe the trend in the data over the three weeks.
Describe the trend in the data over the three weeks.
(i) Draw a line of best fit.
Drawing a line of best fit, we have
(ii) Answer the question specifics.
As we need to describe the trend in the data, we can see that the gradient of the line of best fit is slightly positive (going upwards). This means that the number of people attending the cinema is gradually increasing over the time period.
Note: For this example, the use of a line of best fit significantly limits the accuracy of the trend as it is clear that the data is seasonal (we can see that the number of people attending the cinema on Monday to Thursday each week is lower than for Friday to Sunday).
This is a reason why a moving average would provide a more detailed analysis of the trend.
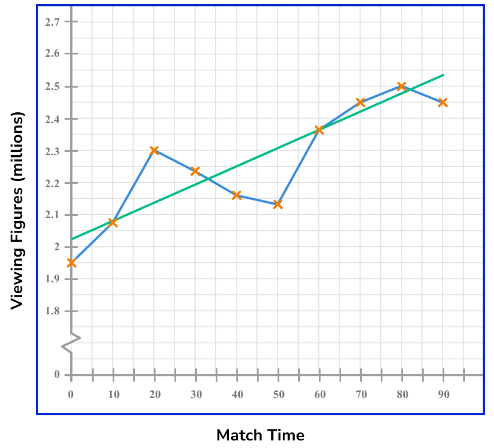
Example 2: Estimate a value within the data range (interpolation)
Below is a time series showing the viewing figures of a football match over 90 minutes, recorded every 10 minutes from the channel FOOTY LIVE.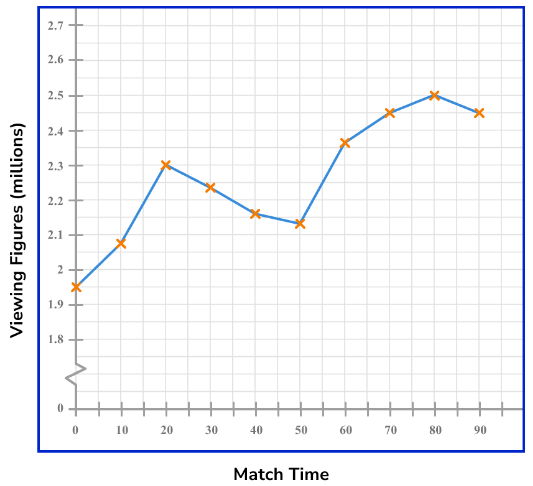 What time would you expect there to be 2.4 million viewers watching the football match on FOOTY LIVE?
What time would you expect there to be 2.4 million viewers watching the football match on FOOTY LIVE?
(i) Draw a line of best fit.
Drawing a line of best fit through the data, we have
(ii) Answer the question specifics.
As we need to estimate the time in which 2.4 million viewers are watching the football match, we need to draw a horizontal line from the 2.4 million viewers value to the trendline, and then a vertical line to locate the estimated time on the horizontal axis.
The time estimated for when 22.4 million viewers were watching the football match on FOOTY LIVE is 67 minutes into the match.
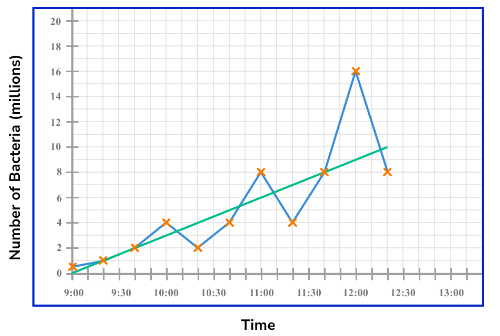
Example 3: estimate a value beyond the data range (extrapolation)
Below is a time series showing the number of bacteria in a petri dish. Every hour, 75% of bacteria are extracted to make a new broth.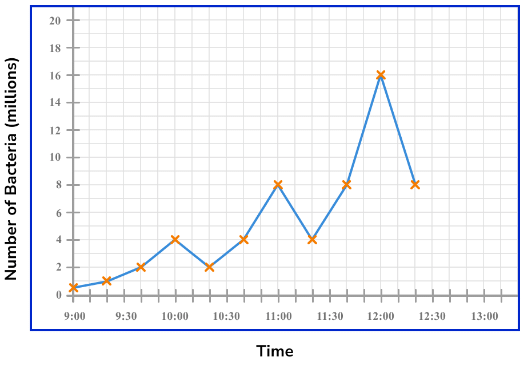
Estimate the number of bacteria in the petri dish at 12:50pm.
(i) Draw a line of best fit.
Drawing a line of best fit through the data, we have
(ii) Answer the question specifics.
As we need to estimate the number of bacteria in the petri dish at 12:50pm, we need to extend the line of best fit until we have a value on the horizontal axis of 12:50pm.
Now that we have a line of best fit for the data, we can draw a vertical line from the value 12:50pm to the line of best fit, and then read the value on the other axis by drawing a horizontal line to this value.
The estimated number of bacteria in the petri dish at 12:50pm is 11.5 million bacteria.
Common Misconceptions
- Points on the time series graph joined using a curve
For the purposes of the time series graphs in GCSE mathematics it is important to use straight line segments to join the points of a time series graph. This can sometimes appear in exams in questions where you will be asked to explain any mistake made on a time series graph. - The horizontal axis is labelled as the variable, with the vertical axis labelled as Time
For a time series, the horizontal axis is always labelled as Time. - The first and last values of the time series are connected to the horizontal axis
It is not always the case where the first and last values are connected to the time series. This is only the case when both of these values are 0. For example, the temperature at midnight could be 0ºC, rise and fall throughout the day, and then be 0ºC at midnight, the following night. This would mean that the values would meet the horizontal axis. - Two values for one time interval
A time series cannot have multiple values for one time period unless you are tracking two different variables. For example, we cannot record two values for the number of entrants to a zoo at 12:30pm but we can record the number of adults and the number of children who have entered a zoo at 12:30pm on the same axis. - The line of best fit is drawn instead of connecting the data values with line segments
The data values are treated as a scatter plot and so they are not connected using line segments. Instead, the line of best fit is drawn, which is incorrect.
Solved Example
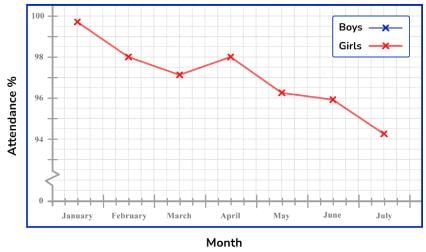
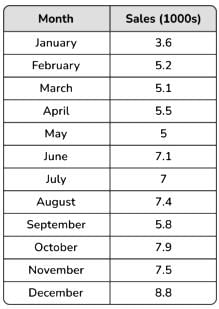
Use the information in the table provided to draw the time series for the Boys attendance on the same set of axes.

Which is the correct time series graph to show this data?
|
137 videos|83 docs|44 tests
|