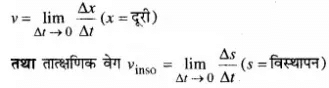सरल रेखा में गति (Motion in a Straight Line) NCERT Solutions | NCERT Textbooks in Hindi (Class 6 to Class 12) - CTET & State TET PDF Download

अभ्यास

प्रश्न.1. नीचे दिए गए गति के कौन-से उदाहरणों में वस्तु को लगभग बिन्दु वस्तु माना जा सकता है
(a) दो स्टेशनों के बीच बिना किसी झटके के चल रही कोई रेलगाड़ी।
(b) किसी वृत्तीय पथ पर साइकिल चला रहे किसी व्यक्ति के ऊपर बैठा कोई बन्दर।
(c) जमीन से टकराकर तेजी से मुड़ने वाली क्रिकेट की कोई फिरकती गेंद।
(d) किसी मेज के किनारे से फिसलकर गिरा कोई बीकर।

(a) रेलगाड़ी दो स्टेशनों के बीच बिना झटके के चल रही है; अत: दोनों स्टेशनों के बीच की दूरी को रेलगाड़ी की लम्बाई की तुलना में अधिक माना जा सकता है। इसलिए रेलगाड़ी को बिन्दु वस्तु माना जाएगा।
(b) चूंकि बन्दर द्वारा यथोचित समय में तय की गई दूरी अधिक है; अत: बन्दर को बिन्दु वस्तु माना जाएगा।
(c) चूंकि गेंद का मुड़ना सरल नहीं है; अतः यथोचित समय में गेंद द्वारा तय की गई दूरी अधिक नहीं है। इसलिए गेंद को बिन्दु वस्तु नहीं माना जा सकत
(d) चूंकि बीकर मेज के किनारे से फिसलकर गिरता है; अतः यथोचित समय में इसके द्वारा तय की गई दूरी अधिक नहीं है। इसलिए इसे बिन्दु वस्तु नहीं माना जा सकता।

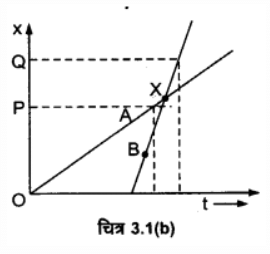
प्रश्न.2. दो बच्चे A व B अपने विद्यालय से लौटकर अपने-अपने घर मे क्रमशः P तथा Q को जा रहे हैं। उनके स्थिति-समय (x - t) + ग्राफ चित्र-3.1 (a) में दिखाए गए हैं। नीचे लिखे कोष्ठकों में सही प्रविष्टियों को चुनिए

(a) B/A की तुलना में A/B विद्यालय से निकट रहता है।
(b) B/A की तुलना में A/B विद्यालय से पहले चलता है।
(c) B/A की तुलना में A/B तेज चलता है।
(d) A और B घर (एक ही/भिन्न) समय पर पहुँचते हैं।
(e) A/B सड़क पर B/A से (एक बार/दो बार) आगे हो जाते हैं।

(a) B की तुलना में A विद्यालय से निकट रहता है, क्योंकि B अधिक दूरी तय करता है [OP< OQ]
(b) B की तुलना में A विद्यालय से पहले चलता है, क्योंकि A के लिए गति प्रारम्भ का समय t  = 0 है परन्तु B के गति प्रारम्भ के लिए समय हैं का निश्चित धनात्मक मान है।

(c) A की तुलना में B तेज चलता है, क्योकि B के ग्राफ का ढाल A के ग्राफ के ढाल से अधिक है।
(d) A और B घर भिन्न समय पर पहुँचते हैं।
(e) B सड़क और A से एक बार आगे हो जाता है (प्रतिच्छेद बिन्दु X के बाद)।

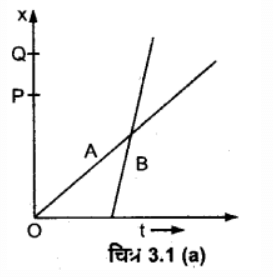
प्रश्न.3. एक महिला अपने घर से प्रातः 9.00 बजे 2.5 km दूर अपने कार्यालय के लिए सीधी सड़क पर 5 kmh^-1 चाल से चलती है। वहाँ वह सायं 5.00 बजे तक रहती है और 25 kmh^-1 की चाल से चल रही किसी ऑटो रिक्शा द्वारा अपने घर लौट आती है। उपयुक्त पैमाना चुनिए तथा उसकी गति का x - t ग्राफ खींचिए।

महिला द्वारा घर से कार्यालय तक पहुँचने में लिया गया समय,

 

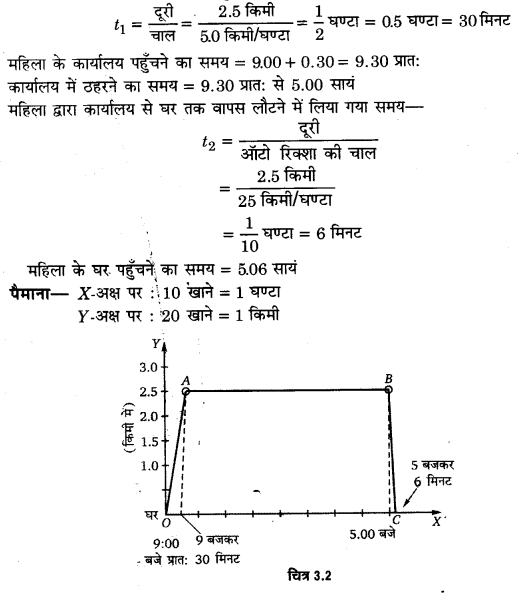
प्रश्न.4. कोई शराबी किसी तंग गली में 5 कदम आगे बढ़ता है और 3 कदम पीछे आता है, उसके बाद फिर 5 कदम आगे बढ़ता है और 3 कदम पीछे आता है, और इसी तरह वह चलता रहता है। उसका हर कदम 1m लम्बा है और 1s समय लगता है। उसकी गति का x-t ग्राफ खींचिए। ग्राफ से तथा किसी अन्य विधि से यह ज्ञात कीजिए कि वह जहाँ से चलना प्रारम्भ करता है वहाँ से 13 m दूर किसी गड्ढे में कितने समय पश्चात गिरता है?

ग्राफ (चित्रे 3.3) से स्पष्ट है कि शराबी गति आरम्भ करने के स्थान से 13 किमी दूर गड्ढे में 37 सेकण्ड बाद
गणना:
प्रथम 8 कदम अर्थात् 8 सेकण्ड में शराबी का गत्यारम्भ के स्थान से विस्थापन अर्थात् उसके द्वारा तय नेट दूरी = (5 – 3) मी = 2 मी
इस प्रकार अगले 8 कदम तक (16 कदमों में) अर्थात्
16 सेकण्ड में नेट दूरी = (2 + 2) मी = 4 मी
24 कदमों में अर्थात् 24 सेकण्ड में नेट दूरी = (2 + 2 + 2) मी = 6 मी 32 कदमों में अर्थात् 32 सेकण्ड में नेट दूरी ।
= (2 + 2 + 2 + 2) मी = 8 मी
37 कदमों में अर्थात् 37 सेकण्ड में नेट दूरी = 8 मी + 5 मी = 13 मी
अतः गत्यारम्भ के स्थान से 13 मी दूर स्थित गड्ढे में गिरने में शराबी द्वारा लिया गया समय = 37 कदमों का समय = 37 सेकण्ड

प्रश्न.5. कोई जेट वायुयान 500 kmh^-1 की चाल से चल रहा है और यह जेट वायुयान के सापेक्ष 1500 kmh^-1 की चाल से अपने दहन उत्पादों को बाहर निकालता है। जमीन पर खड़े किसी प्रेक्षक के सापेक्ष इन दहन उत्पादों की चाल क्या होगी?

जेट का वेग = νJ = – 500 km h^-1 (प्रेक्षक से दूर)
जेट के सापेक्ष दहन उत्पाद बाहर निकालने का आपेक्षिक वेग = νeJ = 1500 km h^-1
यदि बाहर निकलने वाले उत्पादों का वेग νe हो तो νeJ = νe – νJ
या
νe = νeJ + νJ = 1500 + (- 500) = 1000 km/h

प्रश्न.6. सीधे राजमार्ग पर कोई कार126 kmh-1 की चाल से चल रही है। इसे 200 m की दूरी पर रोक दिया जाता है। कार के मन्दन को एकसमान मानिए और इसका मान निकालिए। कार को रुकने में कितना समय लगा?

कार की प्रारम्भिक चाल, u = 126 किमी/घण्टा

 
 

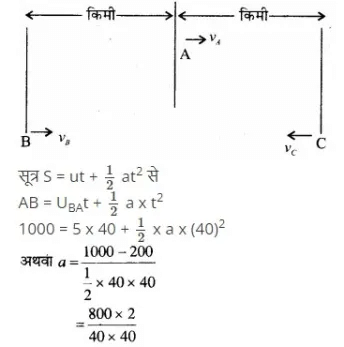
प्रश्न.7. दो रेलगाड़ियाँ A व B दो समान्तर पटरियों पर 72 kmh^-1 की एकसमान चाल से एक ही दिशा में चल रही हैं। प्रत्येक गाड़ी 400 m लम्बी है और गाड़ी A गाड़ी B से आगे है। B का चालक A से आगे निकलना चाहता है तथा 1 ms^-2 से इसे त्वरित करता है। यदि 50s के बाद B को गार्ड A के चालक से आगे हो जाता है तो दोनों के बीच आरम्भिक दूरी कितनी थी?

प्रश्न.8. दो लेन वाली किसी सड़क पर कार A 36 kmh-1 की चाल से चल रही है। एक-दूसरे की विपरीत दिशाओं में चलती दो कारें B वा  C जिनमें से प्रत्येक की चाल 54 kmh-1 है, कार A तक पहुँचना चाहती है। किसी क्षण जब दूरी AB दूरी AC के बराबर है तथा दोनों 1 km हैं, कार B का चालक यह निर्णय करता है कि कार C के कार A तक पहुँचने के पहले ही वह कार A से आगे निकल जाए। किसी दुर्घटना से बचने के लिए कार B का कितना न्यूनतम त्वरण जरूरी है?

दिया है: VA =36 किमी/घण्टा
= 54 x 5 = 15 मीटर/सेकण्ड
माना कार A के सापेक्ष C की आपेक्षिक चाल v_ca तथा कार A के सापेक्ष कार B की आपेक्षिक चाल V_BA है।
∴ V_ca = 15 – (-10) = 25 मीटर/सेकण्ड
तथा V_BA= 15 -10 = 5 मीटर/सेकण्ड
प्रश्नानुसार a_ca = 0, चूँकि दोनों कारें (A व C) नियत वेग से गतिमान हैं।
AC दूरी तय करने में लगा समय

= 1 मीटर प्रति सेकण्डरप्²

प्रश्न.9. दो नगर A व B नियमित बस सेवा द्वारा एक-दूसरे से जुड़े हैं और प्रत्येक मिनट के बाद दोनों तरफ बसें चलती हैं। कोई व्यक्ति साइकिल से 20 kmh^-1 की चाल से A से B की तरफ जा रहा है और यह नोट करता है कि प्रत्येक 18 मिनट के बाद एक बस उसकी गति की दिशा में तथा प्रत्येक 6 मिनट बाद उसके विपरीत दिशा में गुजरती है। बस सेवाकाल T कितना है और बसें सड़क पर किस चाल (स्थिर मानिए) से चलती हैं?

माना प्रत्येक बल की चाल V_b किमी प्रति घण्टा तथा साइकिल सवार की चाल v_c किमी प्रति घण्टा है।
साइकिल सवार की गति की दिशा में अर्थात् A से B की ओर चल रही बसों की आपेक्षिक चाल = V_b – V_c
∴ साइकिल सवार की गति की दिशा में प्रत्येक 18 मिनट बाद एक बस गुजरती है।

प्रश्न.10. कोई खिलाड़ी एक गेंद को ऊपर की ओर आरम्भिक चाल 29 ms^-1 से फेंकता है,
1. गेंद की ऊपर की ओर गति के दौरान त्वरण की दिशा क्या होगी?
2. इसकी गति के उच्चतम बिन्दु पर गेंद के वेग व त्वरण क्या होंगे?
3. गेंद के उच्चतम बिन्दु पर स्थान के समय को x= 0 व t = 0 चुनिए, ऊध्र्वाधर नीचे की ओर की दिशा को X-अक्ष की धनात्मक दिशा मानिए। गेंद की ऊपर की व नीचे की ओर गति के दौरान स्थिति, वेग व त्वरण के चिह्न बताइए।
4. किस ऊँचाई तक गेंद ऊपर जाती है और कितनी देर के बाद गेंद खिलाड़ी के हाथों में आ . जाती है? [g = 9.8m s^-2 तथा वायु का प्रतिरोध नगण्य है।]

1. ऊर्ध्वाधर गति में वस्तु सदैव गुरुत्वीय त्वरण के अधीन चलती है जिसकी दिशा नीचे की ओर होती है।
2. गति के उच्चतम बिन्दु v = 0
a = 9.8 मीटर/सेकण्ड नीचे की ओर

प्रश्न.11. नीचे दिए गए कथनों को ध्यान से पढिए और कारण बताते हुए व उदाहरण देते हुए बताइए कि वे सत्य हैं या असत्य, एकविमीय गति में किसी कण की
(a) किसी क्षण चाल शून्य होने पर भी उसका त्वरण अशून्य हो सकता है।
(b) चाल शून्य होने पर भी उसका वेग अशून्य हो सकता है।
(c) चाल स्थिर हो तो त्वरण अवश्य ही शून्य होना चाहिए।
(d) चाल अवश्य ही बंढती रहेगी, यदि उसका त्वरण धनात्मक हो।

(a) सत्य, सरल आवर्त गति करते कण की महत्तम विस्थापन की स्थिति में कण की चाल शून्य होती है, जबकि त्वरण महत्तम (अशून्य) होता है।
(b) असत्य, चाल शून्य होने का अर्थ है कि कण के वेग का परिमाण शून्य है।
(c) असत्य, एकसमाने वृत्तीय गति करते हुए कण की चाल स्थिर रहती है तो भी उसकी गति में। अभिकेन्द्र त्वरण कार्य करता है।
(d) असत्य, यह केवल जब सत्य हो सकता है जबकि चुनी गई धनात्मक दिशा गति की दिशा के अनुदिश हो।

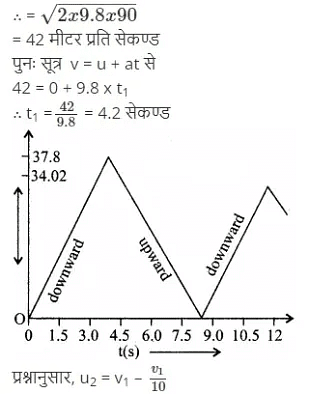
प्रश्न.12. किसी गेंद को 90 m की ऊँचाई से फर्श पर गिराया जाता है। फर्श के साथ प्रत्येक टक्कर में गेंद की चाल 1/10 कम हो जाती है। इसकी गति का t = 0 से 12s के बीच चाल-समय ग्राफ खींचिए।

दिया है: u₁ = 0, s₁ = 90 मीटर,
a₁= 9.8 मीटर/सेकण्ड²
सूत्र v² = u² + 2as से,
v₁² = 0² + 2 x 9.8 x 90

= 42 – 4.2 = 37.8 मीटर/सेकण्ड
v₂ = 0, a₂ = – 9.8 मीटर/सेकण्ड¹
सूत्र v = u + at से
0 = 37.8 – 9.8 x t₂
∴ t₂ = 37.8/9.8
= 3.9 सेकण्ड
t = t₁ + t₂
= 4.2 + 3.9 =8.1 सेकण्ड
u₂ = 0
हम जानते हैं कि, ऊपर जाने का समय = नीचे आने का समय = 3.9 सेकण्ड
∴ t₃ = t₂ = 3.9 सेकण्ड
वह वेग जिससे गेंद फर्श पर टकराती है,
= a₃ = a₂ = 37.8 मीटर/सेकण्ड
तथा t = (t₁ + t₂) + t₃
= 8.1 + 3.9 = 12 सेकण्ड पर
चाल v = 37.8 मीटर/सेकण्ड 

प्रश्न.13. उदाहरण सहित निम्नलिखित के बीच के अन्तर को स्पष्ट कीजिए
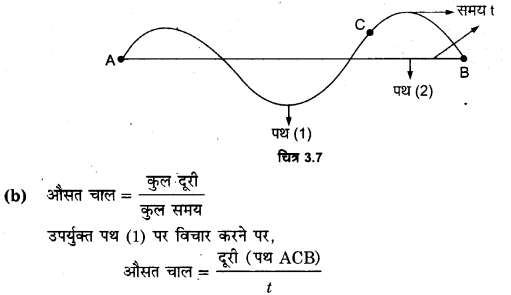
(a) किसी समय अन्तराल में विस्थापन के परिमाण (जिसे कभी-कभी दूरी भी कहा जाता है)। और किसी कण द्वारा उसी अन्तराल के दौरान तय किए गए पथ की कुल लम्बाई।
(b) किसी समय अन्तराल में औसत वेग के परिमाण और उसी अन्तराल में औसत चाल
(किसी समय अंतराल में किसी कण की औसत चाल को समय अन्तराल द्वारा विभाजित की गई कुल पथ-लम्बाई के रूप में परिभाषित किया जाता है। प्रदर्शित कीजिए कि (a) व (b) दोनों में ही दूसरी राशि-पहली से अधिक या उसके बराबर है। समता का चिह्न कब सत्य होता है? (सरलता के लिए केवल एकविमीय गति पर विचार कीजिए।)

(a) विस्थापन के परिमाण का अर्थ है सीधी रेखा की कुल लम्बाई अर्थात् गति के प्रारम्भिक व अन्तिम बिन्दुओं के बीच की दूरी। कण द्वारा किसी समय अन्तराल में तय किए गए निश्चित पथ की कुल लम्बाई, उसी अन्तराल में गति के प्रारम्भिक व अन्तिम बिन्दुओं के बीच की दूरी भिन्न हो सकती है, जैसे चित्र-3.7 में A से B तक पहुँचने में पंथ

(1), दूरी अर्थात् पथ की लम्बाई को तथा पथ

(2) विस्थापन के परिमाण को प्रदर्शित करता है।

स्पष्ट है कि औसत चाल का मान औसत वेग के परिमाण से भिन्न है।

तथा औसत चाल का मान > औसत वेग को परिमाण

यदि A व B के बीच गति केवल पथ (2) पर हो तब औसत चाल =| औसत वेग ।

अतः स्पष्ट है कि प्रत्येक स्थिति में

| औसत चाल | ≥ | औसत वेगे ।

प्रश्न.14. कोई व्यक्ति अपने घर से सीधी सड़क पर 5 kmh^-1 की चाल से 2.5 km दूर बाजार तक पैदल जाता है। परन्तु बाजार बन्द देखकर वह उसी क्षण वापस मुड़ जाता है तथा 7.5 km h^-1 की चाल से घर लौट आता है। समय अन्तराल (i) 0-30 मिनट, (ii) 0-50 मिनट, (iii) 0-40 मिनट की अवधि में उस व्यक्ति (a) के माध्य वेग का परिमाण तथा (b) की माध्य चाल क्या है? (नोट—आप इस उदाहरण से समझ सकेंगे कि औसत चाल को औसत-वेग के परिमाण के रूप में परिभाषित करने की अपेक्षा समय द्वारा विभाजित कुल पथ-लम्बाई के रूप में परिभाषित करना अधिक अच्छा क्यों है? आप थककर घर लौटे उस व्यक्ति को यह बताना नहीं चाहेंगे कि उसकी औसत चाल शून्य थी।)

अर्थात् इस समयान्तराल में व्यक्ति का विस्थापन तथा माध्य वेग के परिमाण भी क्रमश: 2.5 किमी तथा 5 किमी/घण्टा होंगे।
2. 0 – 50 मिनट के समयान्तराल में प्रथम 30 मिनट में व्यक्ति बाजार जाता है जबकि अगले 20 मिनट में वापस आता है।
∴ विस्थापन = 0

3. चूँकि वापस आने में तय दूरी 2.5 किमी तथा लिया गया समय 20 मिनट है। अतः प्रथम 10 मिनट में तय की गई दूरी 1.25 किमी होगी।
अतः 0 – 40 मिनट के समयान्तराल में विस्थापन
= 2.5 – 1.25
= 1.25 किमी

प्रश्न.15. हमने अभ्यास प्रश्न 13तथा 14में औसत चाल व औसत वेग के परिमाण के बीच के अन्तर को स्पष्ट किया है। यदि हम तात्क्षणिक चाल व वेग के परिमाण पर विचार करते हैं तो इस तरह का अन्तर करना आवश्यक नहीं होता। तात्क्षणिक चाल हमेशा तात्क्षणिक वेग के बराबर होती है। क्यों?

हम जानते हैं कि तात्क्षणिक चाल

अर्थात् ∆t → 0 में वस्तु की गति की दिशा को अपरिवर्तित माना जाता है। इस प्रकार कुल पद लम्बाई अर्थात् दूरी एवम् विस्थापन के परिमाण में कोई अन्तर नहीं होता है। अर्थात् तात्क्षणिक चाल हमेशा तात्क्षणिक वेग के परिमाण के तुल्य होती है। 

प्रश्न.16. चित्र-8.8 में (a) से (d) तक के ग्राफों को ध्यान से देखिए और देखकर बताइए कि इनमें से कौन-सा ग्राफ एकविमीय गति को सम्भवतः नहीं दर्शा सकता?

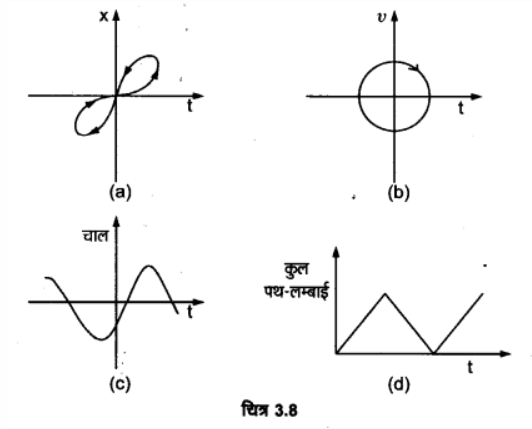
(a) यह ग्राफ एकविमीय गति प्रदर्शित नहीं करता, चूंकि किसी एक क्षण पर कण की दो स्थितियाँ एकविमीय गति में सम्भव नहीं होतीं।
(b) यह ग्राफ एकविमीय गति प्रदर्शित नहीं करता, चूँकि किसी क्षण पर कण का वेग धनात्मक तथा ऋणात्मक दोनों दिशाओं में है, जो एकविमीय गति में सम्भव नहीं है।
(c) यह ग्रफ भी एकविमीय गति प्रदर्शित नहीं करता, चूँकि यह ग्राफ कण की ऋणात्मक चाल व्यक्त कर रहा है तथा कण की चाल ऋणात्मक नहीं हो सकती।
(d) यह ग्राफ भी एकविमीय गति प्रदर्शित नहीं करता, चूँकि यह प्रदर्शित कर रहा है कि कुल पथ की लम्बाई एक निश्चित समय के पश्चात् घट रही है, परन्तु गतिमान कण की कुल पथ-लम्बाई कभी भी समय के साथ नहीं घटती।

प्रश्न.17. चित्र 3.21 में किसी कण की एकविमीय गति का ग्राफ दिखाया गया है। ग्राफ से क्या यह कहना ठीक होगा कि यह कण है t < 0 के लिए किसी सरल रेखा में और है t > 0 के लिए किसी परवलीय पथ में गति करता है। यदि नहीं, तो ग्राफ के संगत किसी उचित भौतिक सन्दर्भ का सुझाव दीजिए।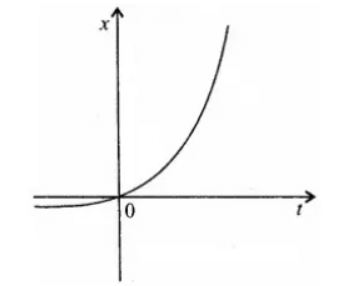

नहीं, यह गलत है। समय-दूरी आलेख (x – t वक्र) किसी कण के प्रक्षेपण को व्यक्त नहीं करता है। जैसे – जब कोई पिण्ड किसी मीनार से गिराया जाता है तब x = 0 पर t = 0 होता है। 

प्रश्न.18. किसी राजमार्ग पर पुलिस की कोई गाड़ी 30 km/h की चाल से चल रही है और यह उसी दिशा में 192 km/h की चाल से जा रही किसी चोर की कार पर गोली चलाती है। यदि गोली की नाल मुखी चाल 150 ms^-1 है तो चोर की कार को गोली किस चाल के साथ आघात करेगी?
(नोट: उस चाल को ज्ञात कीजिए जो चोर की कार को हानि पहुँचाने में प्रासंगिक हो।)

अतः चोर की कार पर प्रहार करते समय गोली की चाल
= पुलिस के सापेक्ष गोली की सापेक्ष चाल – पुलिस के सापेक्ष चोर की कार की सापेक्ष चाल = 150 – 45 = 105 मीटर / सेकण्ड 

प्रश्न.19. चित्र 3.22 में दिखाए गए प्रत्येक ग्राफ के लिए किसी उचित भौतिक स्थिति का सुझाव दीजिए: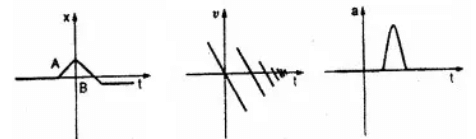

(a) x - t ग्राफ प्रदर्शित कर रहा है कि प्रारम्भ में x शून्य है, फिर यह एक स्थिर मान प्राप्त करता है, पुनः यह शून्य हो जाता है तथा फिर यह विपरीत दिशा में बढ़कर अन्त में एक स्थिर मान (विरामावस्था) प्राप्त कर लेता है। अतः यह ग्राफ इस प्रकार की भौतिक स्थिति व्यक्त कर सकता है जैसे एक गेंद को विरामावस्था से फेंका जाता है और वह दीवार से टकराकर लौटती है तथा कम चाल से उछलती है तथा यह क्रम इसके विराम में पहुँचने तक चलता रहता है।
(b) यह ग्राफ प्रदर्शित कर रहा है कि वेग समय के प्रत्येक अन्तराल के साथ परिवर्तित हो रहा है तथा प्रत्येक बार इसका वेग कम हो रहा है। इसलिए यह ग्राफ एक ऐसी भौतिक स्थिति को व्यक्त कर सकता है जिसमें एक स्वतन्त्रतापूर्वक गिरती हुई गेंद (फेंके जाने पर) धरती से टकराकर कम चाल से पुनः उछलती है तथा प्रत्येक बार धरती से टकराने पर इसकी चाल कम होती जाती है।
(c) यह ग्राफ प्रदर्शित करता है कि वस्तु अल्प समय में ही त्वरित हो जाती है। अत: यह ग्राफ एक ऐसी भौतिक स्थिति को व्यक्त कर सकता है जिसमें एकसमान चाल से चलती हुई गेंद को अत्यल्प समयान्तराल में बल्ले द्वारा टकराया जाता है।

प्रश्न.20. चित्र 3.23 में किसी कण की एकविमीय सरल आवर्ती गति के लिए x - t ग्राफ दिखाया गया है। (इस गति के बारे में आप अध्याय 14 में पढ़ेंगे) समय t = 0.3 s, 1.2 s, – 1.2s पर कण के स्थिति, वेग व त्वरण के चिह्न क्या होंगे?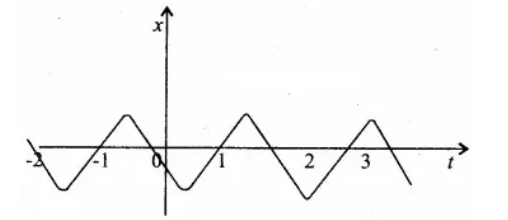

हम जानते हैं कि सरल आवर्त गति में,
त्वरण a = – w²x
जहाँ w नियतांक है जिसे कोणीय आवृत्ति कहते हैं।
समय t = 0.3 सेकण्ड दर, दूरी (x) ऋणात्मक है। दूरी – समय ग्राफ का दाब भी ऋणात्मक है। इस कारण स्थिति तथा वेग ऋणात्मक है। अतः त्वरण (a = – w²x) धनात्मक है।
समय t = 1.2 सेकण्ड पर, दूरी (x) धनात्मक है। दूरी समय (x – t) ग्राफ का ढाल भी धनात्मक है। इस प्रकार स्थिति तथा वेग धनात्मक है। अतः त्वरण ऋणात्मक है।
समय t = – 1.2 सेकण्ड पर, दूरी (x) ऋणात्मक है। दूरी समय (x – t) ग्राफ का ढाल भी धनात्मक है। इस प्रकार वेग धनात्मक है तथा अन्त में त्वरण (a) भी धनात्मक है।

प्रश्न.21. चित्र 3.24 में किसी कण की एकविमीय गति का है ग्राफ दर्शाता है। इसमें तीन समान अन्तराल दिखाए गए हैं। किस अन्तराल में औसत चाल अधिकतम है और किसमें न्यूनतम है? प्रत्येक अन्तराल के लिए औसत वेग का चिह्न बताइए।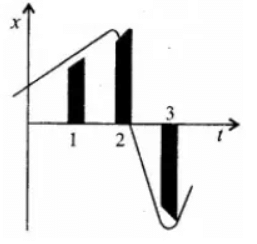

चूँकि लघु अन्तरालों में समय – दूरी (x – t) ग्राफ की ढाल उस अन्तराल में कण की औसत चाल को प्रदर्शित करती है। ग्राफ से स्पष्ट है कि इस अन्तराल में,

1. अन्तराल (3) में ग्राफ की ढाल अधिकतम है अत: औसत चाल अधिकतम है। जबकि अन्तराल (2) में ग्राफ की ढाल न्यूनतम है अतः इस अन्तराल में औसत चाल न्यूनतम है।
2. अन्तराल (1) एवम् (2) में ढाल धनात्मक है लेकिन अन्तराल (3) में ऋणात्मक है अतः अन्तराल (1 व 2) में औसत वेग धनात्मक जबकि अन्तराल (3) में ऋणात्मक है।

प्रश्न.22. चित्र 3.25 में किसी नियत (स्थिर) दिशा के अनुदिश चल रहे कण.का चाल-समय ग्राफ दिखाया गया है। इसमें तीन समान समय अन्तराल दिखाए गए हैं। किस अन्तराल में औसत त्वरण का परिमाण अधिकतम होगा? किस अन्तराल में औसत चाल अधिकतम होगी? धनात्मक दिशा को गति की स्थिर दिशा चुनते हुए तीनों अन्तरालों में ν तथा a के चिह्न बताइए। A, B, C व D बिन्दुओं पर त्वरण क्या होंगे?

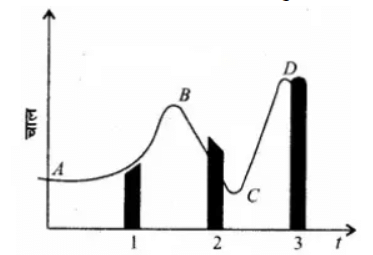
1. चूँकि लघु अन्तरालों में चाल-समय (v-1) ग्राफ की ढाल का परिमाण कण के औसत त्वरण के परिमाण को व्यक्त करता है। दिए गए ग्राफ से स्पष्ट है कि ढाल का परिमाण अन्तराल वक्र (2) में अधिकतम जबकि अन्तराल (3) में न्यूनतम है। इस प्रकार औसत त्वरण का परिमाण अन्तराल (2) में अधिकतम व अन्तराल (3) में न्यूनतम होगा।
2. औसत चाल अन्तराल (1) में न्यूनतम तथा अन्तराल (3) में अधिकतम है।
3. तीनों अन्तरालों में चाल (v) धनात्मक है। अन्तराल (1) में चाल-समय (v – t) ग्राफ का ढाल धनात्मक जबकि अन्तराल (2) में ढाल अर्थात् त्वरण a ऋणात्मक है। अन्तराल (3) में चाल – समय ग्राफ समय-अक्ष के समान्तर है। अतः इस अन्तराल में त्वरण शून्य है।.
4. चारों बिन्दुओं (i.e., A, B, C तथा D) पर, चाल – समय ग्राफ समय-अक्ष के समान्तर है। अतः इन चारों बिन्दुओं पर त्वरण शून्य है।