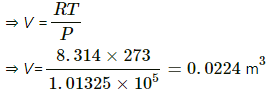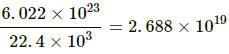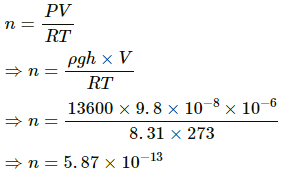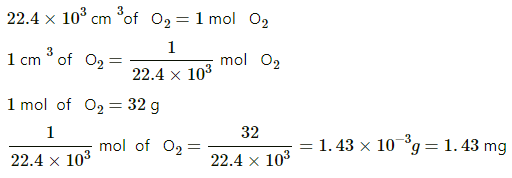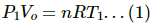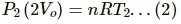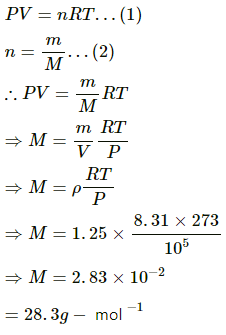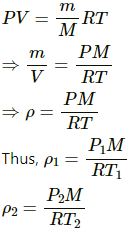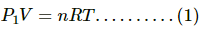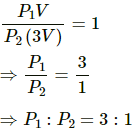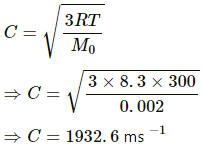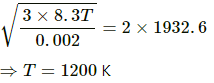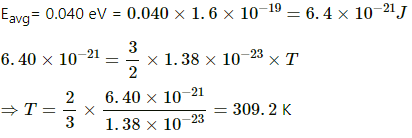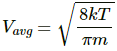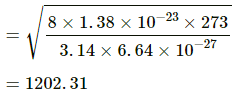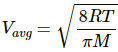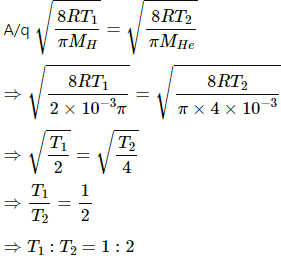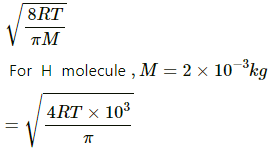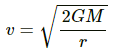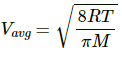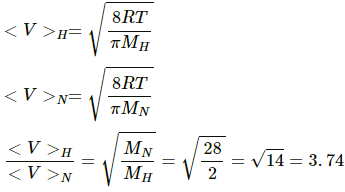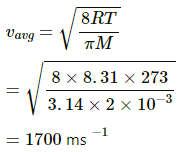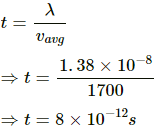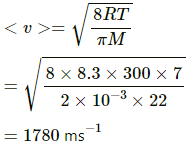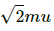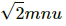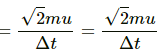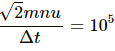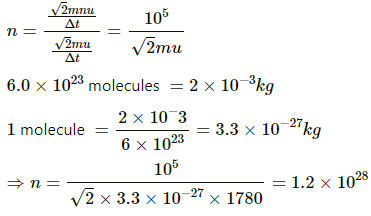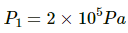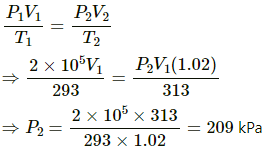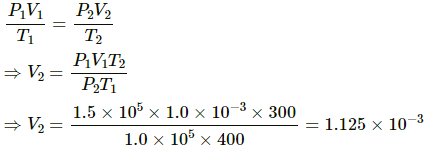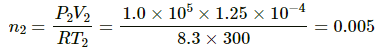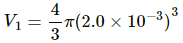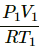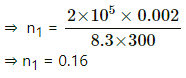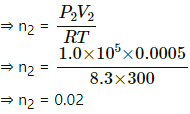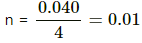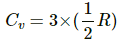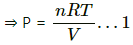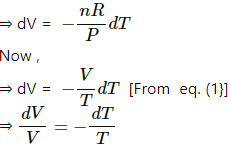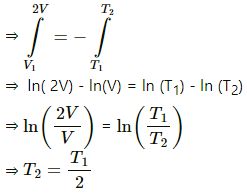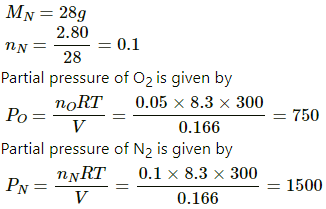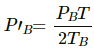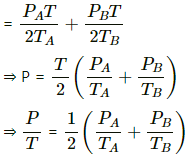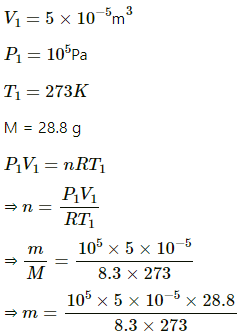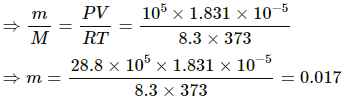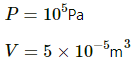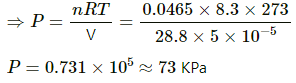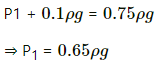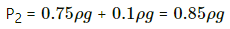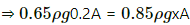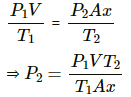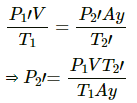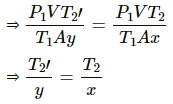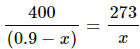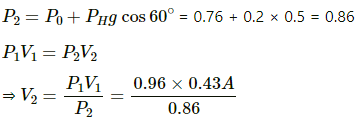HC Verma Questions and Solutions: Chapter 24: Kinetic Theory of Gases- 2 | HC Verma Solutions - JEE PDF Download
Exercises
Q.1. Calculate the volume of 1 mole of an ideal gas at STP.
Here, STP means a system having a temperature of 273 K and 1 atm pressure.
Pressure, P = 1.01325 × 05 Pa
No of moles, n = 1 mol
Temperature, T = 273 K
Applying the equation of an ideal gas, we get
PV = nRT
Q.2. Find the number of molecules of an ideal gas in a volume of 1.000 cm3 at STP.
Here,
Volume of ideal gas at STP = 22.4 L
Number of molecules in 22.4 L of ideal gas at STP = 6.022×1023
Number of molecules in 22.4×103 cm3 of ideal gas at STP = 6.022×1023
Now,
Number of molecules in 1 cm3 of ideal gas at STP =
Q.3. Find the number of molecules in 1 cm3 of an ideal gas at 0°C and at a pressure of 10−5mm of mercury.
Use R = 8.31 J K-1 mol-1.
Given:
Volume of ideal gas, V = 1 cm3 = 10-6 m3
Temperature of ideal gas, T = 0 °C = 273 K
Pressure of mercury, P = 10−8 m of Hg
Density of ideal gas, ρ = 13600 kgm-3
Pressure (P) is given by
P = ρgh
Here,
ρ = density of ideal gas
g = acceleration due to gravity,
Using the ideal gas equation, we get
Number of molecules = N × n
= 6.023 × 1023×5.874 × 10−13
= 35.384 × 1010
= 3.538 × 1011
Q.4. Calculate the mass of 1 cm3 of oxygen kept at STP.
We know that 22.4 L of O2 contains 1 mol O2 at STP. Thus,
Q.5. Equal masses of air are sealed in two vessels, one of volume V0 and the other of volume 2V0. If the first vessel is maintained at a temperature 300 K and the other at 600 K, find the ratio of the pressures in the two vessels.
Use R = 8.31 JK-1 mol-1.
Let the pressure and temperature for the vessels of volume V0 and 2V0 be P1, T1 and P2 , T2, respectively.
Since the two vessels have the same mass of gas, n1 = n2 = n.
T1 = 300K
T2 = 600KUsing the equation of state for perfect gas, we get PV = nRT
For the vessel of volume V0 :
For the vessel of volume 2 V0:
Dividing eq. (2) by eq. (1), we get
Q.6. An electric bulb of volume 250 cc was sealed during manufacturing at a pressure of 10−3 mm of mercury at 27°C. Compute the number of air molecules contained in the bulb. Avogadro constant = 6 × 1023 mol−1, density of mercury = 13600 kg m−3 and g = 10 m s−2.
Use R=8.314J K-1 mol-1
Given:
Volume of electric bulb, V = 250 cc
Temperature at which manufacturing takes place, T = 27 + 273 = 300 K
Height of mercury, h = 10−3 mm
Density of mercury, ρ 13600 kgm−3
Avogadro constant, N = 6 × 1023 mol−1
Pressure (P) is given by
Using the ideal gas equation, we get
Q.7. A gas cylinder has walls that can bear a maximum pressure of 1.0 × 106 Pa. It contains a gas at 8.0 × 105 Pa and 300 K. The cylinder is steadily heated. Neglecting any change in the volume, calculate the temperature at which the cylinder will break.
Given:-
Maximum pressure that the cylinder can bear, Pmax = 1.0 × 106 Pa
Pressure in the gas cylinder, P1 = 8.0 × 105 Pa
Temperature in the cylinder, T1 = 300 K
Let T2 be the temperature at which the cylinder will break.
Volume is constant. Thus, .....(Given)
V1= V2 = V
Applying the five variable gas equation, we get
Q.8. 2 g of hydrogen is sealed in a vessel of volume 0.02 m3 and is maintained at 300 K. Calculate the pressure in the vessel.
Use R=8.3J K-1 mol-1.
Given:
Mass of hydrogen, m = 2 g
Volume of the vessel, V = 0.02 m3
Temperature in the vessel, T = 300 K
Molecular mass of the hydrogen, M = 2 u
No of moles, n = m/M = 2/2 = 1 mole
Rydberg's constant, R = 8.3 J/Kmol
From the ideal gas equation, we get
PV = nRT
⇒ P = 1.24 × 105 Pa
Q.9. The density of an ideal gas is 1.25 × 10−3 g cm−3 at STP. Calculate the molecular weight of the gas.
Use R=8.31J K-1 mol-1.
Let:
m = Mass of the gas
M = Molecular mass of the gas
Now,
Density of ideal gas, ρ= 1.25 × 10−3 gcm−3 =1.25 kgm−3
Pressure, P = 1.01325 × 105 Pa (At STP)
Temperature, T = 273 K (At STP)
Using the ideal gas equation, we get
Q.10. The temperature and pressure at Simla are 15.0°C and 72.0 cm of mercury and at Kalka these are 35.0°C and 76.0 cm of mercury. Find the ratio of air density at Kalka to the air density at Simla.
Use R=8.314J K-1 mol-1.
Here,
Temperature in Simla, T1= 15 + 273 = 288 K
Pressure in Simla, P1 = 0.72 m of Hg
Temperature in Kalka, T2= 35+273 = 308 K
Pressure in Kalka, P2 = 0.76 m of Hg
Let density of air at Simla and Kalka be ρ1 and ρ2 respectively. Then,
Taking ratios , we get
Q.11. Figure shows a cylindrical tube with adiabatic walls and fitted with a diathermic separator. The separator can be slid in the tube by an external mechanism. An ideal gas is injected into the two sides at equal pressures and equal temperatures. The separator remains in equilibrium at the middle. It is now slid to a position where it divides the tube in the ratio of 1:3. Find the ratio of the pressures in the two parts of the vessel.
Use R=8.314J K-1 mol-1
Since the separator initially divides the cylinder equally, the number of moles of gas are equal in the two parts. Thus,
n1 = n2= n
Volume of the first part = V
Volume of the second part =3V
It is given that the walls are diathermic. So, temperature of the two parts is equal. Thus,
T1 = T2 = T
Let pressure of first and second parts be P1 and P2, respectively.
For first part:- Applying equation of state, we get
For second part:- Applying equation of state, we get
Dividing eq. (1) by eq. (2), we get
Q.12. Find the rms speed of hydrogen molecules in a sample of hydrogen gas at 300 K. Find the temperature at which the rms speed is double the speed calculated in the previous part.
Use R=8.314 JK-1 mol-1
Here,
Temperature of hydrogen gas, T = 300 K
Molar mass of hydrogen, M0 = 2 g/mol=0.002 kg /mol
We know,
In the second case, let the required temperature be T.
Applying the same formula, we get
Q.13. A sample of 0.177 g of an ideal gas occupies 1000 cm3 at STP. Calculate the rms speed of the gas molecules.
Here,
V = 10-3 m3
Density = 0.177 kgm-3
P = 105pa
Q.14. The average translational kinetic energy of air molecules is 0.040 eV (1 eV = 1.6 × 10−19J). Calculate the temperature of the air. Boltzmann constant k = 1.38 × 10−23 J K−1.
We know from kinetic theory of gases that the average translational energy per molecule is 3/2 kT.
Now,
Q.15. Consider a sample of oxygen at 300 K. Find the average time taken by a molecule to travel a distance equal to the diameter of the earth.
Use R=8.314 JK-1 mol-1
Here,
Q.16. Find the average magnitude of linear momentum of a helium molecule in a sample of helium gas at 0°C. Mass of a helium molecule = 6.64 × 10−27 kg and Boltzmann constant = 1.38 × 10−23 J K−1.
Here,
m = 6.64 × 10−27 kg
T = 273 K
Average speed of the He atom is given by
We know,
Momentum = m × Vavg
= 6.64 × 10−27 × 1201.35
= 7.97 × 10−24
= 8 × 10−24 kg-m/s
Q.17. The mean speed of the molecules of a hydrogen sample equals the mean speed of the molecules of a helium sample. Calculate the ratio of the temperature of the hydrogen sample to the temperature of the helium sample.
Use R = 8.314 JK-1 mol-1
Mean velocity is given by
Let temperature for H and He respectively be T1 and T2, respectively.
For hydrogen:
MH = 2g = 2 × 10-3 kg
For helium:
MHe= 4 g = 4 × 10-3 kg
Now,
Q.18. At what temperature the mean speed of the molecules of hydrogen gas equals the escape speed from the earth?
Use R = 8.314 JK-1 mol-1
Mean speed of the molecule is givne by
For escape velocity of Earth :-
Let r be the radius of Earth
Multiplying numerator and denominator by R, we get
Q.19. Find the ratio of the mean speed of hydrogen molecules to the mean speed of nitrogen molecules in a sample containing a mixture of the two gases.
Use R = 8.314 JK-1 mol-1
we know,
Molar mass of H2 = MH = 2×10-3 kg
Molar mass of N2 = MN = 28×10-3 kg
Now,
Q.20. Figure shows a vessel partitioned by a fixed diathermic separator. Different ideal gases are filled in the two parts. The rms speed of the molecules in the left part equals the mean speed of the molecules in the right part. Calculate the ratio of the mass of a molecule in the left part to the mass of a molecule in the right part.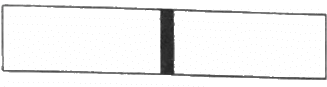
Let the temperature of gas in both the chambers be T.
Let the molar mass of gas in the left chamber and right chamber be M1 and M2, respectively.
Let mass of gas in the left and right chamber be m1 and m2, respectively. Then,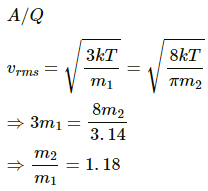
Q.21. Estimate the number of collisions per second suffered by a molecule in a sample of hydrogen at STP. The mean free path (average distance covered by a molecule between successive collisions) = 1.38 × 10−5 cm.
Use R = 8.31 JK-1 mol-1.
Here,
Average speed of the H molecules is given by
The time between two collisions is given by
Number of collisions in 1s =
Q.22. Hydrogen gas is contained in a closed vessel at 1 atm (100 kPa) and 300 K. (a) Calculate the mean speed of the molecules. (b) Suppose the molecules strike the wall with this speed making an average angle of 45° with it. How many molecules strike each square metre of the wall per second?
Use R = 8.31 JK-1 mol-1.
Here,
P = 105 Pa
T = 300 K
For H2
M = 2×10-3 kg
(a) Mean speed is given by
Let us consider a cubic volume of 1m3.
V = 1 m3
Momentum of 1 molecule normal to the striking surface before collision = mu sin 45°
Momentum of 1 molecule normal to the striking surface after collision = - mu sin 45°
Change in momentum of the molecule = 2mu sin 45° =
Change in momentum of n molecules = 2mnu sin 45° =
Let Δt be the time taken in changing the momentum.
Force per unit area due to one molecule
Observed pressure due to collision by n molecules =
Q.23. Air is pumped into an automobile tyre's tube up to a pressure of 200 kPa in the morning when the air temperature is 20°C. During the day the temperature rises to 40°C and the tube expands by 2%. Calculate the pressure of the air in the tube at this temperature.
Here,
P2 = ?
T1 = 293 K
T2 = 313 K
V2 = V1 + 0.02 V1 = V1 (1.02)
Now,
Q.24. Oxygen is filled in a closed metal jar of volume 1.0 × 10−3 m3 at a pressure of 1.5 × 105Pa and temperature 400 K. The jar has a small leak in it. The atmospheric pressure is 1.0 × 105 Pa and the atmospheric temperature is 300 K. Find the mass of the gas that leaks out by the time the pressure and the temperature inside the jar equalise with the surrounding.
Here,
V1 = 1.0 × 10-3 m3
T1 = 400K
P1 = 1.5 × 105 Pa
P2 = 1.0 × 105 Pa
T2 = 300
M = 32 g
Number of moles in the jar before
Volume of the gas when pressure becomes equal to external pressure is given by
Net volume of leaked gas = V2 - V1
= 1.125 × 10-3 - 1.0 × 10-3
= 1.25 × 10-4 m3
Let n2 be the number of moles of leaked gas. Applying equation of state on this amount of gas, we get
Mass of leaked gas = 32 × 0.005 = 0.16 g
Q.25. An air bubble of radius 2.0 mm is formed at the bottom of a 3.3 m deep river. Calculate the radius of the bubble as it comes to the surface. Atmospheric pressure = 1.0 × 105 Pa and density of water = 1000 kg m−3.
Here,
h = 3.3 m
P1 = Po + ρgh
⇒ P1 = 1.0 × 105 + 1000 × 9.8 × 3.3
⇒ P1 = 1.32 × 105 Pa
P2 = 1.0 × 105 Pa
Since temperature remains the same, applying Boyle's law we get
P1 V1 = P2 V2
Let R2 be the new radius. Then,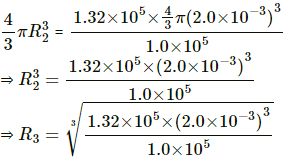
⇒ R3 = 2.2 × 10-3 m
Q.26. Air is pumped into the tubes of a cycle rickshaw at a pressure of 2 atm. The volume of each tube at this pressure is 0.002 m3. One of the tubes gets punctured and the volume of the tube reduces to 0.0005 m3. How many moles of air have leaked out? Assume that the temperature remains constant at 300 K and that the air behaves as an ideal gas.
Use R = 8.3 J K-1 mol-1
Here,
P1 = 2 × 105 pa
V1 = 0.002 m3
V2 = 0.0005 m3
T1 = T2 = 300 K
Number of moles initially, n1 =
Applying equation of state, we get
P2 V2 = n2 RT
Assuming the final pressure becomes equal to the atmospheric pressure, we get
P2 = 1.0 × 105 pa
Number of leaked moles= n2 - n1
= 0.16 -0.02
= 0.14
Q.27. 0.040 g of He is kept in a closed container initially at 100.0°C. The container is now heated. Neglecting the expansion of the container, calculate the temperature at which the internal energy is increased by 12 J.
Use R = 8.3 J K-1 mol-1.
Here ,
m = 0.040g
M = 4g
T1 = (100 + 273) K = 373 K
He is a monoatomic gas. Thus,
⇒ Cv = 1.5 × 8.3 = 12.45
Let the initial internal energy be U1 .
Let the final internal energy be U2 .
U2 -U1 = n Cv ( T2 -T1 )
⇒ 0.01 × 12.45( T2 - 373) = 12
⇒ T2 = 469 K
The temperature in °C can be obtained as follows: 469 - 273 = 196° C.
Q.28. During an experiment, an ideal gas is found to obey an additional law pV2 = constant. The gas is initially at a temperature T and volume V. Find the temperature when it expands to a volume 2V.
Use R = 8.3 J K-1 mol-1
Applying equation of state of an ideal gas, we get
PV = nRT
Taking differentials, we get
⇒ PdV + VdP = nRdT . . . 2
Applying the additional law, we get
PV2 = c
V2 dP + 2VPdV = 0
⇒ VdP + 2PdV = 0 . . . 3
Subtracting eq. (3) from eq. (2) , we get
PdV = -nRdT
Integrating between T2 and T1 , we get
Q.29. A vessel contains 1.60 g of oxygen and 2.80 g of nitrogen. The temperature is maintained at 300 K and the volume of the vessel is 0.166 m3. Find the pressure of the mixture.
Use R = 8.3 J K-1 mol-1.
Here,
V = 0 .166 m3
T = 300 K
Mass of O2 = 1.60 g
MO = 32 g
nO = 1.60/32 = 0.05
Mass of N2 = 2.80 g
Total pressure is sum of the partial pressures.
⇒ P = PN + PO = 750 + 1500 = 2250 Pa
Q.30. A vertical cylinder of height 100 cm contains air at a constant temperature. The top is closed by a frictionless light piston. The atmospheric pressure is equal to 75 cm of mercury. Mercury is slowly poured over the piston. Find the maximum height of the mercury column that can be put on the piston.
Here,
h = 1 m
P1 = 0.75 mHg = 0.75 ρg Pa
ρ = 13500 kg/m3
Let h be the height of the mercury above the piston.
P2 = P1 + hρg
Let the CSA be A.
V1 = Ah = A
V2 = (1 - h)A
Applying Boyle's law, we get
P1 V1 = P2 V2
⇒ 0.75 ρgA = P2 (1 - h)A
⇒ 0.75 ρg = (0.75 ρg + hρg)(1 - h)
⇒ 0.75 = (0.75 + h)(1 - h)
⇒ h = 0.25 m
h = 25 cm
Q.31. Figure shows two vessels A and B with rigid walls containing ideal gases. The pressure, temperature and the volume are pA, TA, V in the vessel A and pB, TB, V in the vessel B. The vessels are now connected through a small tube. Show that the pressure p and the temperature T satisfy 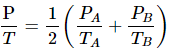 when equilibrium is achieved.
when equilibrium is achieved.
Let the partial pressure of the gas in chamber A and B be P'A and P'B , respectively.
Applying equation of state for gas A, we get
Similarly, For gas B :
Total Pressure is the sum of the partial pressures . It is given by
P = P'A + P'B
Q.32. A container of volume 50 cc contains air (mean molecular weight = 28.8 g) and is open to atmosphere where the pressure is 100 kPa. The container is kept in a bath containing melting ice (0°C). (a) Find the mass of the air in the container when thermal equilibrium is reached. (b) The container is now placed in another bath containing boiling water (100°C). Find the mass of air in the container. (c) The container is now closed and placed in the melting-ice bath. Find the pressure of the air when thermal equilibrium is reached.
Use R = 8.3 J K-1 mol-1.
(a) Here ,
⇒ m = 0.0635 g
(b) Here,
M = 28.8 g
Applying equation of state , we get
PV = nRT
Thus, mass of expelled air = 0.017 g
Amount of air in the container = 0.0635 - 0.017 = 0.0465 g
(c) Here,
T = 273K
Applying equation of state, we get
PV = nRT
Q.33. A uniform tube closed at one end, contains a pellet of mercury 10 cm long. When the tube is kept vertically with the closed-end upward, the length of the air column trapped is 20 cm. Find the length of the air column trapped when the tube is inverted so that the closed-end goes down. Atmospheric pressure = 75 cm of mercury.
Let the CSA of the tube be A .
Initial volume of air , V1 = 20A cm = 0.2A
Length of mercury , h = 0.1 m
Let the pressure of the trapped air when the tube is inverted and vertical be P1.
Now , Pressure of the mercury and trapped air balances the atmospheric pressure . Thus ,
when the tube is inverted with the closed end down , the pressure acting upon the trapped air is
Atmospheric pressure + Mercury column pressure
Now ,
Pressure of trapped air = Atmospheric Pressure + Mercury column Pressure [In equilibrium]
Applying the Boyle's law when the temperature remains constant , we get
P1 V1 = P2V2
Let the new height of the trapped air be x .
⇒ x = 0.15 m = 15 cm
Q.34. A glass tube, sealed at both ends, is 100 cm long. It lies horizontally with the middle 10 cm containing mercury. The two ends of the tube contain air at 27°C and at a pressure 76 cm of mercury. The air column on one side is maintained at 0°C and the other side is maintained at 127°C. Calculate the length of the air column on the cooler side. Neglect the changes in the volume of mercury and of the glass.
Let CSA of the tube be A.
on the colder side :
P1 = 0.76 m Hg
T1 = 300K
V1 = V
T2 = 273K
V2 = Ax
on the hotter side :
P1= 0.76 m Hg
T1 = 300K
V1' = V
T2' = 400K
V2' = Ay
In equilibrium , the pressures on both side will balance each other.
⇒ P2' = P2
From the length of the tube , we get
x + y + 0.1=1
⇒ y = 0.9-x
⇒ x = 0.365 m
⇒ x = 36.5 cm
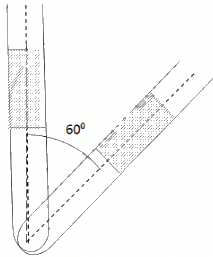
Q.35. An ideal gas is trapped between a mercury column and the closed-end of a narrow vertical tube of uniform base containing the column. The upper end of the tube is open to the atmosphere. The atmospheric pressure equals 76 cm of mercury. The lengths of the mercury column and the trapped air column are 20 cm and 43 cm respectively. What will be the length of the air column when the tube is tilted slowly in a vertical plane through an angle of 60°? Assume the temperature to remain constant.
Here,
Initial pressure = Atmospheric pressure + pressure due to mercury
⇒ P1 = P0 + PHg
Let the CSA of the tube be A.
P1 = 0.76 + 0.2 = 0.96 m Hg
T1 = T2 = T
V1 = 0.43 A
If the tube is slanted , then the atmospheric pressure P0 remains the same . only the PHg changes
Let the length of the air column be l.
⇒ l = 0.48 m
⇒ l = 48 cm
|
134 docs
|
FAQs on HC Verma Questions and Solutions: Chapter 24: Kinetic Theory of Gases- 2 - HC Verma Solutions - JEE
| 1. What is the kinetic theory of gases? |  |
| 2. How does the kinetic theory of gases explain pressure? |  |
| 3. What is the relationship between temperature and the average kinetic energy of gas particles? |  |
| 4. How does the kinetic theory of gases explain the volume and shape of gases? |  |
| 5. Can the kinetic theory of gases be applied to real gases? |  |