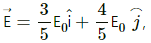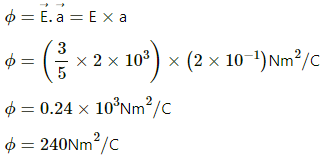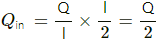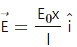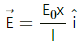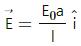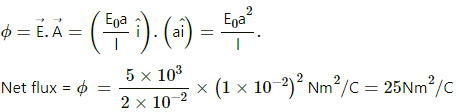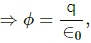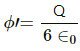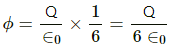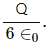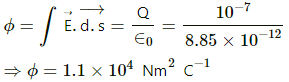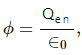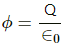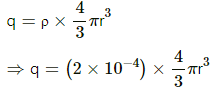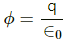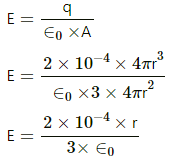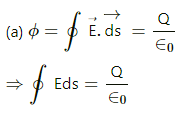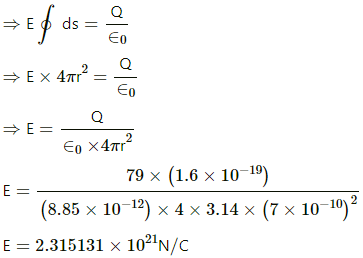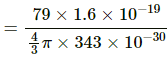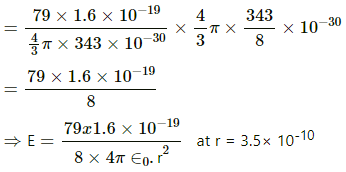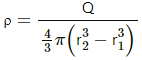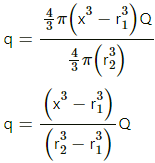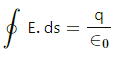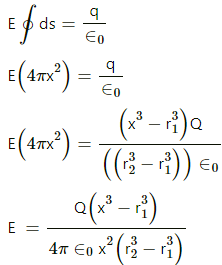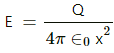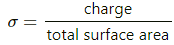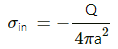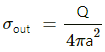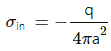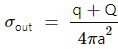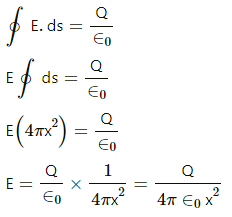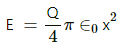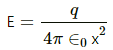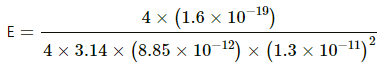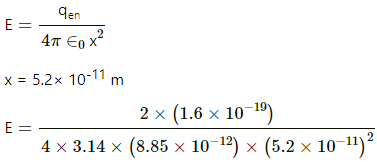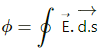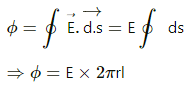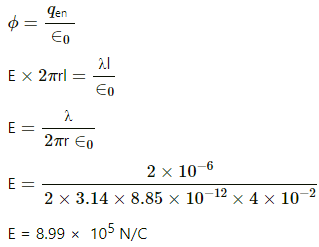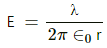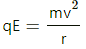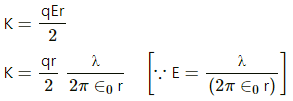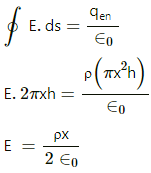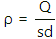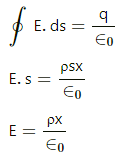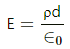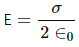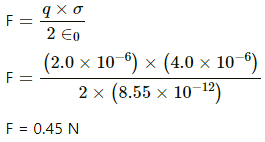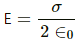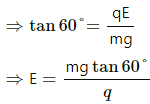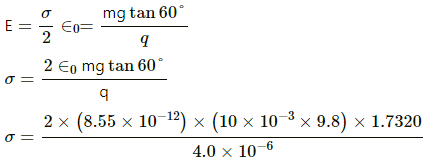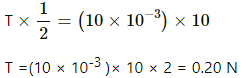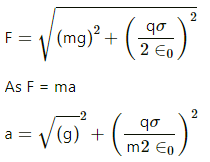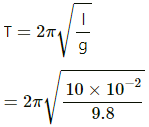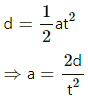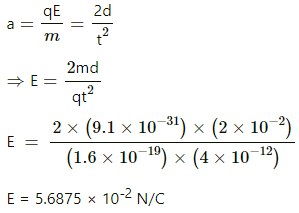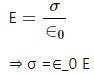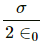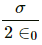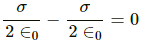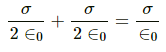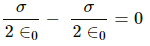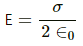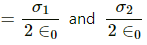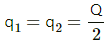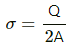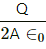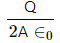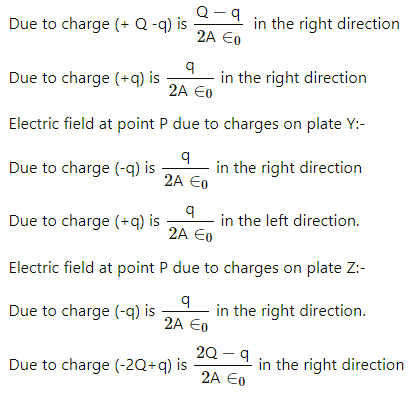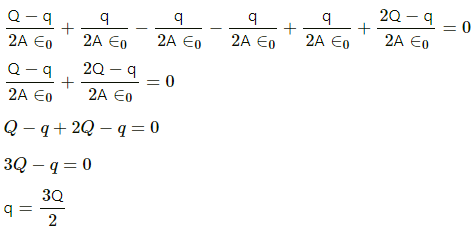HC Verma Questions and Solutions: Chapter 30: Gauss’s Law- 2 | HC Verma Solutions - JEE PDF Download
Exercises
Q.1. The electric field in a region is given by 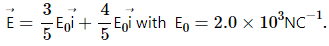
Find the flux of this field through a rectangular surface of area 0⋅2 m2 parallel to the y-z plane.
Given:
Electric field strength
where E0 = 2.0 103 N/C
he plane of the rectangular surface is parallel to the y-z plane. The normal to the plane of the rectangular surface is along the x axis. Onlypasses perpendicular to the plane; so, only this component of the field will contribute to flux.
On the other hand,moves parallel to the surface.
Surface area of the rectangular surface, a = 0⋅2 m2
Flux,
Q.2. A charge Q is uniformly distributed over a rod of length l. Consider a hypothetical cube of edge l with the centre of the cube at one end of the rod. Find the minimum possible flux of the electric field through the entire surface of the cube.
Given:
Total charge on the rod = Q
The length of the rod = edge of the hypothetical cube = l
Portion of the rod lying inside the cube, x = I/2
Linear charge density for the rod = Q/I
Using Gauss's theorem, flux through the hypothetical cube,
Ø = (Qin/∈0) , where Qin = charge enclosed inside the cube
Here, charge per unit length of the rod = Q/I
Charge enclosed,
Therefore,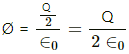
Q.3. Show that there can be no net charge in a region in which the electric field is uniform at all points.
It is given that the electric field is uniform. If we consider a surface perpendicular to the electric field, we find that it is an equipotential surface. Hence, if a test charge is introduced on the surface, then work done will be zero in moving the test charge on it.
But if there is some net charge in this region, the test charge introduced on the surface will experience a force due to this charge. This force has a component parallel to the surface; thus, work has to be done in moving this test charge. Thus, the surface cannot be said to be equipotential. This implies that the net charge in the region with uniform electric field is zero.
Q.4. The electric field in a region is given by 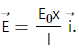
Find the charge contained inside the cubical volume bound by the surfaces x =0, x =a, y=0, y=a, z=0 and z=a. Take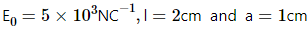
Given:
Electric field strength,
Length, l = 2 cm
Edge of the cube, a = 1 cm
E0 =5.0 × 103 N/C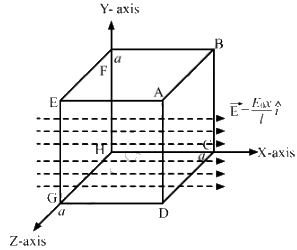
It is observed that the flux passes mainly through the surfaces ABCD and EFGH. The surfaces AEFB and CHGD are parallel to the electric field. So, electric flux for these surfaces is zero.
The electric field intensity at the surface EFGH will be zero.
If the charge is inside the cube, then equal flux will pass through the two parallel surfaces ABCD and EFGH. We can calculate flux passing only through one surface. Thus,
At EFGH, x = 0; thus, the electric field at EFGH is zero.
At ABCD, x = a; thus, the electric field at ABCD is
The net flux through the whole cube is only through the side ABCD and is given by
Thus the net charge,
q = ∈0∅
q = 8.85 × 10 -12 × 25
q =22.125 ×10-13
q =2.2125 ×10 -12 C
Q.5. A charge Q is placed at the centre of a cube. Find the flux of the electric field through the six surfaces of the cube.
According to Gauss's Law, flux passing through any closed surface is equal to
tin the charge enclosed by that surface.
where ϕ is the flux through the closed surface and q is the charge enclosed by that surface.
The charge is placed at the centre of the cube and the electric field is passing through the six surfaces of the cube.
∴ So, we can say that the total electric flux passes equally through these six surfaces .
Thus, flux through each surface,
Q.6. A charge Q is placed at a distance a/2 above the centre of a horizontal, square surface of edge a as shown in the following figure . Find the flux of the electric field through the square surface.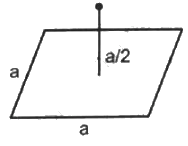
Given:-
Edge length of the square surface = a
Distance of the charge Q from the square surface = a/2
Area of the plane = a2
Assume that the given surface is one of the faces of the imaginary cube.
Then, the charge is found to be at the centre of the cube.
A charge is placed at a distance of about a/2 from the centre of the surface.
The electric field due to this charge is passing through the six surfaces of the cube.
Hence flux through each surface,
Thus, the flux through the given surface is
Q.7. Find the flux of the electric field through a spherical surface of radius R due to a charge of 10−7 C at the centre and another equal charge at a point 2R away from the centre in the following figure.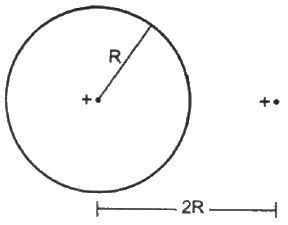
Given:-
Let charge Q be placed at the centre of the sphere and Q' be placed at a distance 2R from the centre.
Magnitude of the two charges = 10−7 C
According to Gauss's Law, the net flux through the given sphere is only due to charge Qthat is enclosed by it and not by the charge Q' that is lying outside.
So, only the charge located inside the sphere will contribute to the flux passing through the sphere.
Thus,
Q.8. A charge Q is placed at the centre of an imaginary hemispherical surface. Using symmetry arguments and Gauss's Law, find the flux of the electric field due to this charge through the surface of the hemisphere in the following figure.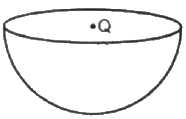
From Guass's law, flux through a closed surface,
where
Qen = charge enclosed by the closed surface
Let us assume that a spherical closed surface in which the charge is enclosed is Q.
The flux through the sphere,
Hence for a hemisphere(open bowl), total flux through its curved surface,
Q.9. A spherical volume contains a uniformly distributed charge of density 2.0 × 10 -4 Cm-3 Find the electric field at a point inside the volume at a distance 4⋅0 cm from the centre.
Given :
Volume charge density, ρ = 2 ×10-4 C /m3
Let us assume a concentric spherical surface inside the given sphere with radius = 4 cm = 4 ×10-2 m
The charge enclosed in the spherical surface assumed can be found by multiplying the volume charge density with the volume of the sphere. Thus,
The net flux through the spherical surface,
The surface area of the spherical surface of radius r cm:
A = 4πr2
Electric field,
The electric field at the point inside the volume at a distance 4⋅0 cm from the centre,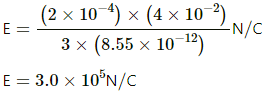
Q.10. The radius of a gold nucleus (Z = 79) is about 7.0 × 10-10 m. Assume that the positive charge is distributed uniformly throughout the nuclear volume. Find the strength of the electric field at (a) the surface of the nucleus and (b) at the middle point of a radius. Remembering that gold is a conductor, is it justified to assume that the positive charge is uniformly distributed over the entire volume of the nucleus and does not come to the outer surface?
Given:
Atomic number of gold = 79
Charge on the gold nucleus, Q = 79 × (1.6 ×10-19) C The charge is distributed across the entire volume. So, using Gauss's Law, we get:
The value of E is fixed for a particular radius.
(b) To find the electric field at the middle point of the radius:
Net charge =79 ×1.6 ×10-19 C
Volume charge density
So, the charge enclosed by this imaginary sphere of radius r =3.5× 10 -10.
= 1.16 × 1021 N/C.
As electric charge is given to a conductor, it gets distributed on its surface. But nucleons are bound by the strong force inside the nucleus. Thus, the nuclear charge does not come out and reside on the surface of the conductor. Thus, the charge can be assumed to be uniformly distributed in the entire volume of the nucleus.
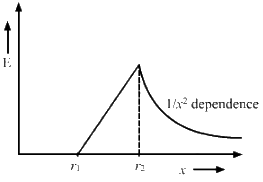
Q.11. A charge Q is distributed uniformly within the material of a hollow sphere of inner and outer radii r1 and r2 (see the figure). Find the electric field at a point P at a distance x away from the centre for r1 < x < r. Draw a rough graph showing the electric field as a function of x for 0 < x < 2r2 (see the figure).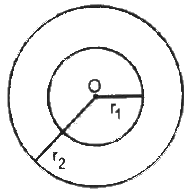
Amount of charge present on the hollow sphere = Q
Inner radii of the hollow sphere = r1
Outer radii of the hollow sphere = r2
Consider an imaginary sphere of radius x.
The charge on the sphere can be found by multiplying the volume charge density of the hollow spherical volume with the volume of the imaginary sphere of radius (x-r1).
Charge per unit volume of the hollow sphere,
Charge enclosed by this imaginary sphere of radius x:-
q = ρ × Volume of the part consisting of charge
According to Gauss's Law,
Here, the surface integral is carried out on the sphere of radius x and q is the charge enclosed by this sphere.
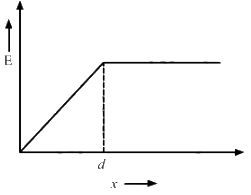
The electric field is directly proportional to x for r1 < x < r.
The electric field for r2 < x < 2r2,
Thus, the graph can be drawn as:-
Q.12. A charge Q is placed at the centre of an uncharged, hollow metallic sphere of radius a. (a) Find the surface. (b) If a charge q is put on the sphere, what would be the surface charge densities on the inner and outer surfaces? (c) Find the electric field inside the sphere at a distance x from the centre in the situations (a) and (b).
Given:
Amount of charge present at the centre of the hollow sphere = Q
We know that charge given to a hollow sphere will move to its surface.
Due to induction, the charge induced at the inner surface = −Q
Thus, the charge induced on the outer surface = +Q
(a)
Surface charge density is the charge per unit area, i.e.
Surface charge density of the inner surface,
Surface charge density of the outer surface,
(b) Now if another charge q is added to the outer surface, all the charge on the metal surface will move to the outer surface. Thus, it will not affect the charge induced on the inner surface. Hence the inner surface charge density,
As the charge has been added to the outer surface, the total charge on the outer surface will become (Q+q).
So the outer surface charge density,
(c) To find the electric field inside the sphere at a distance x from the centre in both the situations,let us assume an imaginary sphere inside the hollow sphere at a distance x from the centre.
Applying Gauss's Law on the surface of this imaginary sphere,we get:
Here, Q is the charge enclosed by the sphere.
For situation (b):
As the point is inside the sphere, there is no effect of the charge q given to the shell.
Thus, the electric field at the distance x:
Q.13. Consider the following very rough model of a beryllium atom. The nucleus has four protons and four neutrons confined to a small volume of radius 10−15 m. The two 1 selectrons make a spherical charge cloud at an average distance of 1⋅3 ×10−11 m from the nucleus, whereas the two 2 s electrons make another spherical cloud at an average distance of 5⋅2 × 10−11 m from the nucleus. Find three electric fields at (a) a point just inside the 1 s cloud and (b) a point just inside the 2 s cloud.
(a) Let us consider the three surfaces as three concentric spheres A, B and C.
Let us take q = 1.6× 10-19 C .
Sphere A is the nucleus; so, the charge on sphere A, q1 = 4q
Sphere B is the sphere enclosing the nucleus and the 2 1s electrons; so charge on this sphere, q2 = 4q -2q = 2q
Sphere C is the sphere enclosing the nucleus and the 4 electrons of Be; so, the charge enclosed by this sphere,
q3 = 4q -4q = 0
Radius of sphere A, r1 = 10-15 m
Radius of sphere B, r2 = 1.3 × 10-11 m
Radius of sphere C, r3 = 5.2 × 10-11 m
As the point 'P' is just inside the spherical cloud 1s, its distance from the centre
x = 1.3 × 10-11 m
Electric field,
Here, the charge enclosed is due to the charge of the 4 protons inside the nucleus . So,
E = 3.4× 1013 N/C
(b) For a point just inside the 2s cloud, the total charge enclosed will be due to the 4 protons and 2 electrons. Charge enclosed, qen = 2q = 2× (1.6 ×10-19) C
Hence, electric field,
E = 1.065 × 1012 N/C
Thus , E =1.1× 1012 N/C.
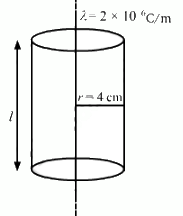
Q.14. Find the magnitude of the electric field at a point 4 cm away from a line charge of density 2 × 10-6 Cm-1.
Given:
Charge density of the line containing charge, λ = 2 × 10-6 C/m-1
We need to find the electric field at a distance of 4 cm away from the line charge.
We take a Gaussian surface around the line charge of cylindrical shape of radius r = 4 ×10-2 m and height l.
The charge enclosed by the Gaussian surface, qen = λl
Let the magnitude of the electric field at a distance of 4 cm away from the line charge be E.
Thus, net flux through the Gaussian surface,
There will be no flux through the circular bases of the cylinder; there will be flux only from the curved surface.
The electric field lines are directed radially outward, from the line charge to the cylinder.
Therefore, the lines will be perpendicular to the curved surface.
Thus,
Applying Gauss's theorem,
Q.15. A long cylindrical wire carries a positive charge of linear density 2.0 × 10-8 C m -1 An electron revolves around it in a circular path under the influence of the attractive electrostatic force. Find the kinetic energy of the electron. Note that it is independent of the radius.
Let the linear charge density of the wire be λ.
The electric field due to a charge distributed on a wire at a perpendicular distance rfrom the wire,
The electrostatic force on the electron will provide the electron the necessary centripetal force required by it to move in a circular orbit. Thus,
⇒ mv2 = qEr .. (1)
Kinetic energy of the electron,`"K" = 1/2 mv2`
From (1),
K =(1.6 ×10-19) × ( 2 × 10-8) × ( 9 × 109)J
K = 2.88 × 10-17 J
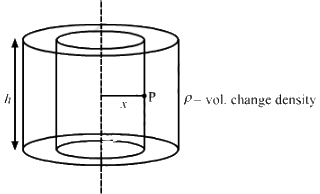
Q.16. A long cylindrical volume contains a uniformly distributed charge of density ρ. Find the electric field at a point P inside the cylindrical volume at a distance x from its axis (see the figure).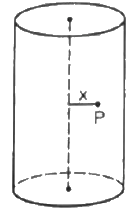
Given:-
Volume charge density inside the cylinder = ρ
Let the radius of the cylinder be r.
Let charge enclosed by the given cylinder be Q
Consider a Gaussian cylindrical surface of radius x and height h.
Let charge enclosed by the cylinder of radius x be q'.
The charge on this imaginary cylinder can be found by taking the product of the volume charge density of the cylinder and the volume of the imaginary cylinder. Thus, q' = ρ( π x2 h)
From Gauss's Law,
Q.17. A non-conducting sheet of large surface area and thickness d contains a uniform charge distribution of density ρρ. Find the electric field at a point P inside the plate, at a distance x from the central plane. Draw a qualitative graph of E against x for 0 < x < d.
Given:
Thickness of the sheet = d
Let the surface area of the sheet be s.
Volume of the sheet = sd
Volume charge density of the sheet,
Charge on the sheet = Q
Consider an imaginary plane at a distance x from the central plane of surface area s.
Charge enclosed by this sheet, q =ρsx
For this Guassian surface, using Gauss's Law,we get:
The electric field outside the sheet will be constant and will be:
Q.18. A charged particle with a charge of −2⋅0 × 10−6 C is placed close to a non-conducting plate with a surface charge density of 4.0 × 10-6Cm0-2. Find the force of attraction between the particle and the plate.
The electric field due to a conducting thin sheet,
The magnitude of attractive force between the particle and the plate,
F =qE
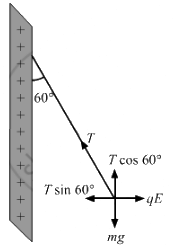
Q.19. One end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non-conducting plate and the other end is fastened to a small ball of mass 10 g and a charge of 4.0× 10-6 C. In equilibrium, the thread makes an angle of 60° with the vertical. Find the surface charge density on the plate.
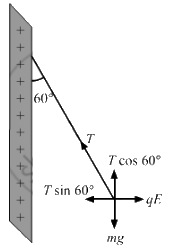
There are two forces acting on the ball. These are
(1) Weight of the ball, W = mg
(2) Coulomb force acting on the charged ball due to the electric field of the plate, F = qE
Due to these forces,a tension develops in the thread.
Let the surface charge density on the plate be σ.
Electric field of a plate,
It is given that in equilibrium, the thread makes an angle of 60° with the vertical.
Resolving the tension in the string along horizontal and vertical directions, we get:
T cos 60° = mg
T sin 60° = qE
Also, electric field due to a plate,
σ = 7.5× 10-7 C/m2
Q.20. One end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non-conducting plate and the other end is fastened to a small ball of mass 10 g and a charge of 4.0× 10-6 C. In equilibrium, the thread makes an angle of 60° with the vertical (a) Find the tension in the string in equilibrium. (b) Suppose the ball is slightly pushed aside and released. Find the time period of the small oscillations.
(a)
In equilibrium state, the thread makes an angle of 60o with the vertical.
The tension in the thread is resolved into horizontal and vertical components.
Then, tension in the string in equilibrium,
T cos 60° = mg
(b) As it is displaced from equilibrium, net force on the ball,
The surface charge density of the plate (as calculated in the previous question), σ = 7.5×10-7 C/m2
Charge on the ball, q = 4×10-6 C
Mass of the ball, m =
The time period of oscillation of the given simple pendulum,
= 0.45 sec
Q.21. Two large conducting plates are placed parallel to each other with a separation of 2⋅00 cm between them. An electron starting from rest near one of the plates reaches the other plate in 2⋅00 microseconds. Find the surface charge density on the inner surfaces.
Distance travelled by the electron, d= 2 cm
Time taken to cross the region, t = 2× 10-6 s
Let the surface charge density at the conducting plates be σ.
Let the acceleration of the electron be a.
Applying the 2nd equation of motion, we get:
This acceleration is provided by the Coulombic force. So,
Also, we know that electric field due to a plate,
⇒ σ = ( 8.85 × 10-12) × ( 5.68 × 10-2 ) C/m2
⇒ σ = 50.33 × 10-14 C/m2 = 0.503 × 10-12 C/m2
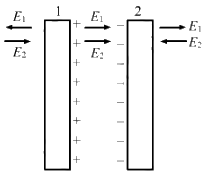
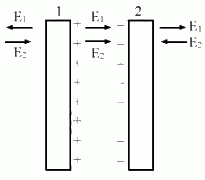
Q.22. Two large conducting plates are placed parallel to each other and they carry equal and opposite charges with surface density σ as shown in the figure. Find the electric field (a) at the left of the plates (b) in between the plates and (c) at the right of the plates.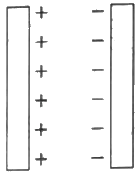
Given:-
Surface charge density on the plates = σ
The electric field due to plate 1, E1 =
The electric field due to plate 2, E2 =
(a) The strength of the electric field due to both the plates will be same but their directions will be opposite to each other on any point at the left of the two plates.
Thus, the net electric field at a point on the left of plate1 =
(b) Here the direction of the fields will be same. So, they will add up to give the resultant field in this region.
Total electric field:-
(c) The strength of the electric field due to both the plates will be same but their directions will be opposite to each other at any point on the right of the two plates.
Thus, the net electric field at a point on the left of plate 2 =
Q.23. Two conducting plates X and Y, each with a large surface area A (on one side), are placed parallel to each other, as shown in the following figure . Plate X is given a charge Q,whereas the other is kept neutral. Find (a) the surface charge density at the inner surface of plate X (b) the electric field at a point to the left of the plates (c) the electric field at a point in between the plates and (d) the electric field at a point to the right of the plates.
(a) Given that the charge present on the plate is Q. The other plate will get the same charge Q due to convection.
Let the surface charge densities on both sides of the plate be σ1 and σ2.
Now, electric field due to a plate,
So, the magnitudes of the electric fields due to this plate on each side
The plate has two sides, each of area A. So, the net charge given to the plate will be equally distributed on both the sides. This implies that the charge developed on each side will be
This implies that the net surface charge density on each side = Q/2A
(b) Electric field to the left of the plates
On the left side of the plate surface, charge density,
Hence, electric field =
This must be directed towards the left, as 'X' is the positively-charged plate.
(c) Here, the charged plate 'X' acts as the only source of electric field, with positive in the inner side. Plate Y is neutral. So, a negative charge will be induced on its inner side. 'Y' attracts the charged particle towards itself. So, the middle portion E is towards the right and is equal to
(d) Similarly for the extreme right, the outer side of plate 'Y' acts as positive and hence it repels to the right with
Q.24. Three identical metal plates with large surface areas are kept parallel to each other as shown in the following figure. The leftmost plate is given a charge Q, the rightmost a charge −2Q and the middle one is kept neutral. Find the charge appearing on the outer surface of the rightmost plate.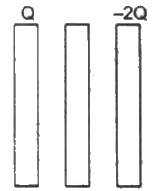
Consider the Gaussian surface as shown in the figure.
Let the charge on the outer surface of the left-most plate be q. Thus, the charges on the plates are distributed as shown in the following diagram.
The net field at point P due to all the induced charges must be zero, as it is lying inside the metal surface.
Let the surface area of the plates be A.
Electric field at point P due to the charges on plate X:-
The net electric field at point P:-
Thus, the charge on the outer plate of the right-most plate =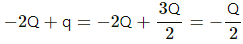
|
134 docs
|