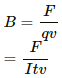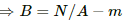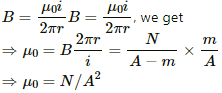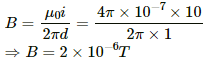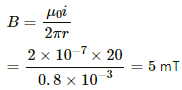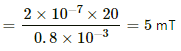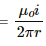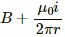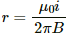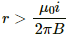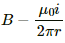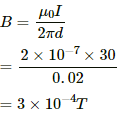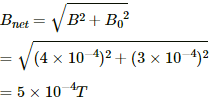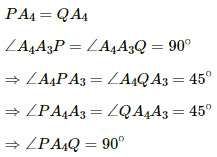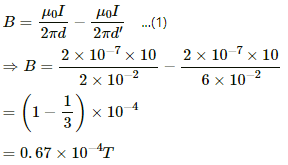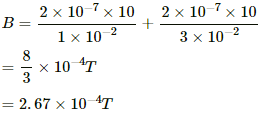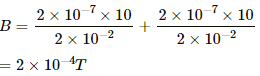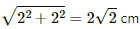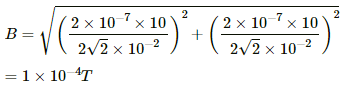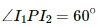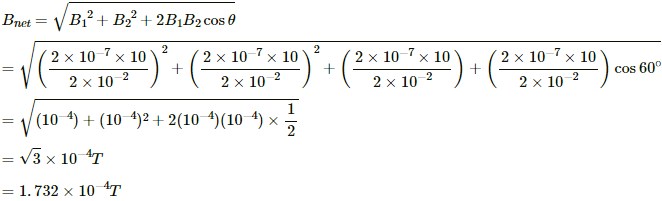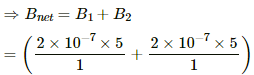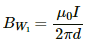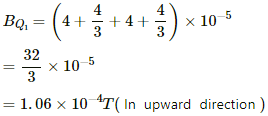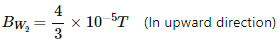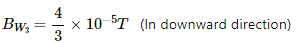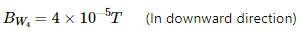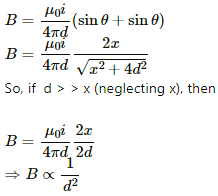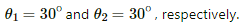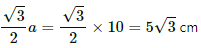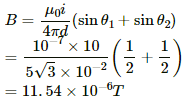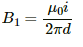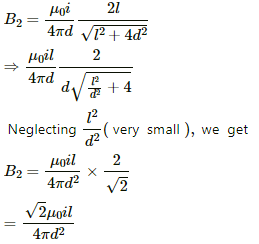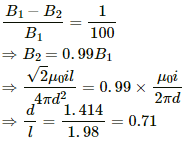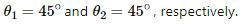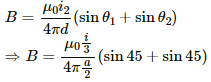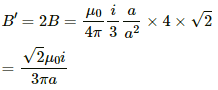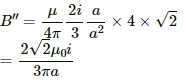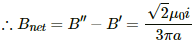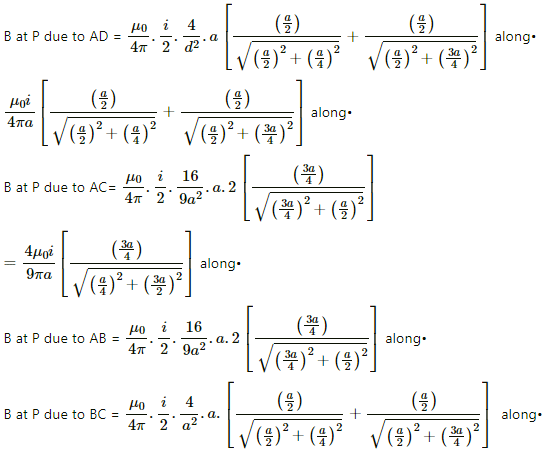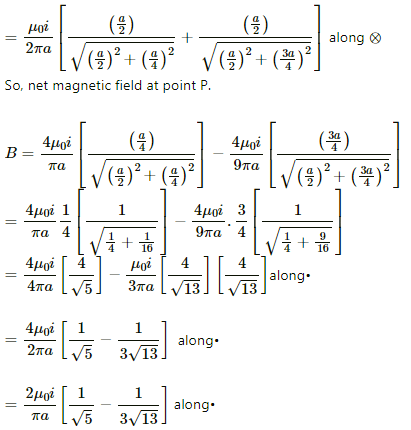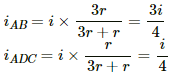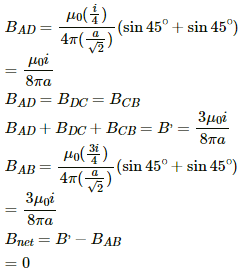HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 2 | HC Verma Solutions - JEE PDF Download
Exercises
Q.1. Using the formula 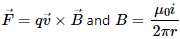 show that the SI units of the magnetic field B and the permeability constant µ0 may be written as N mA−1 and NA−2 respectively.
show that the SI units of the magnetic field B and the permeability constant µ0 may be written as N mA−1 and NA−2 respectively.
Using the relation
we get
Units of
Force (F) = N
Current (I) = A
Time (T) = s
Velocity (v) = m/s
Now, using the relation
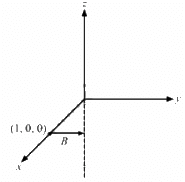
Q.2. A current of 10 A is established in a long wire along the positive z-axis. Find the magnetic field 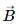 at the point (1 m, 0, 0).
at the point (1 m, 0, 0).
Given:
Magnitude of current, I = 10 A
Separation of the point from the wire, d = 1 m
The magnetic fieldat point (1 m, 0, 0) is given by
(Along the +ve y-axis by the right-hand thumb rule)
Q.3. A copper wire of diameter 1.6 mm carries a current of 20 A. Find the maximum magnitude of the magnetic field 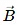 due to this current.
due to this current.
Given:
Magnitude of current, I = 10 A
Diameter of the wire, d = 1.6 × 10−3 m
∴ Radius of the wire = 0.8 × 10−3 m
The magnetic field intensity is given by
Q.4. A transmission wire carries a current of 100 A. What would be the magnetic field B at a point on the road if the wire is 8 m above the road?
Given:
Magnitude of current, I = 100 A
Separation of the road from the wire, d = 8 m
Thus, the magnetic field is given by
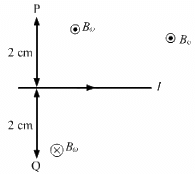
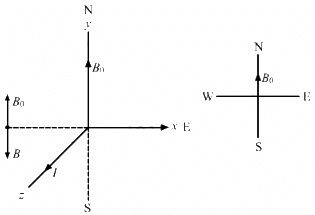
Q.5. A long, straight wire carrying a current of 1.0 A is placed horizontally in a uniform magnetic field B = 1.0 × 10−5 T pointing vertically upward figure. Find the magnitude of the resultant magnetic field at the points P and Q, both situated at a distance of 2.0 cm from the wire in the same horizontal plane.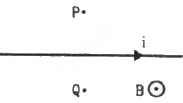
Given:
Uniform magnetic field, B0 = 1.0 × 10−5 T (Vertically upwards)
Separation of the point from the wire, d = 2 cm = 0.02 m
The magnetic field due to the wire is given by
Now,
Net magnetic field at point P:
BP = Bw + B0 = 2 × 10−5 T
Net magnetic field at point Q:
BQ = Bw − B0 = 0
Q.6. A long, straight wire of radius r carries a current i and is placed horizontally in a uniform magnetic field B pointing vertically upward. The current is uniformly distributed over its cross section. (a) At what points will the resultant magnetic field have maximum magnitude? What will be the maximum magnitude? (b) What will be the minimum magnitude of the resultant magnetic field?
(a) As the wire in question is carrying current, so it will also generate a magnetic field around it. And for a long straight wire it will be maximum at the mid-point called P.
Now,
Magnetic field generated by the current carrying wire
Net magnetic field =
(b) Magnetic field B = 0
Clearly,
B = 0
when
But when
Net magnetic field =
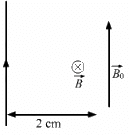
Q.7. A long, straight wire carrying a current of 30 A is placed in an external, uniform magnetic field of 4.0 × 10−4 T parallel to the current. Find the magnitude of the resultant magnetic field at a point 2.0 cm away from the wire.
Given:
Uniform magnetic field, B0 = 4.0 × 10−4 T
Magnitude of current, I = 30 A
Separation of the point from the wire, d = 0.02 m
Thus, the magnetic field due to current in the wire is given by
B0 is perpendicular to B (as shown in the figure).
∴ Resultant magnetic field
Q.8. A long, vertical wire carrying a current of 10 A in the upward direction is placed in a region where a horizontal magnetic field of magnitude 2.0 × 10−3 T exists from south to north. Find the point where the resultant magnetic field is zero.
Given:
Uniform magnetic field, B0 = 2.0 × 10−3 T (From south to north)
To make the resultant magnetic field zero, the magnetic field due to the wire should be of the same magnitude as B0 and in the direction north to south.
The above condition will be satisfied when the required point will be placed in the west w.r.t. the wire.
Let the separation of the point from the wire be d.
The magnetic field due to current in the wire is given by
From the question, B = B0.
Q.9. Figure shows two parallel wires separated by a distance of 4.0 cm and carrying equal currents of 10 A along opposite directions. Find the magnitude of the magnetic field B at the points A1, A2, A3.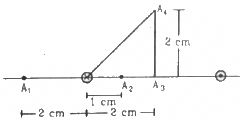
For point A1,
Magnitude of current in wires, I = 10 A
Separation of point A1 from the wire on the left side, d = 2 cm
Separation of point A1 from the wire on the right side, d' = 6 cm
In the figure
Red and blue arrow denotes the direction of magnetic field due to the wire marked as red and blue respectively.
P (marked red) denotes the wire carrying current in a plane going into the paper.
Q (marked blue) denotes the wire carrying current in a plane coming out of the paper.
Also from the figure, we can see that
The magnetic field at A1 due to current in the wires is given by
Similarly, we get the magnetic field at A2 using eq. (1).
Now,
Magnetic field at A3:
Magnetic field at A4:
Separation of point A4 from the wire on the left side, d =
Separation of point A4 from the wire on the right side, d' =
Thus, the magnetic field at A4 due to current in the wires is given by
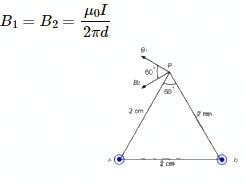
Q.10. Two parallel wires carry equal currents of 10 A along the same direction and are separated by a distance of 2.0 cm. Find the magnetic field at a point which is 2.0 cm away from each of these wires.
Given:
Magnitude of currents, I1 = I2 = 10 A
Separation of the point from the wires, d = 2 cm
Thus, the magnetic field due to current in the wire is given by
In the figure, dotted circle shows the magnetic field lines due to current carrying wire placed in a plane perpendicular to the plane of the paper.
From the figure, we can see thatis an equilateral triangle.
Angle between the magnetic fields due to current in the wire, θ = 60°
∴ Required magnetic field at P
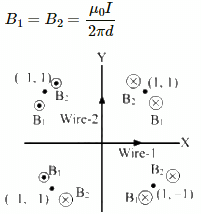
Q.11. Two long, straight wires, each carrying a current of 5 A, are placed along the x- and y-axis respectively. The currents point along the positive directions of the axes. Find the magnetic fields at the points (a) (1 m, 1 m), (b) (−1 m, 1 m), (c) (−1 m, −1 m) and (d) (1 m, −1 m).
Given:
Magnitude of current, I = 5 A
Separation of the point from the wire, d = 1 m
Thus, the magnitude of magnetic field due to current in the wires is given by
(a) At point (1 m, 1 m), the magnetic fields due to the wires are the same in magnitude, but they are opposite in direction.
Hence, the net magnetic field is zero.
(b) At point (−1 m, 1 m), the magnetic fields due to the wires are in upward direction.
= 2 × 10−6 T (Along the z-axis)
(c) At point (−1 m, −1 m), the magnetic fields due to the wires are the same in magnitude, but they are opposite in direction.
Hence, the net magnetic field is zero.
(d) At point (1 m, −1 m), the magnetic fields due to the wires are in upward direction.
= 2 × 10−6 T (Along the negative z-axis)
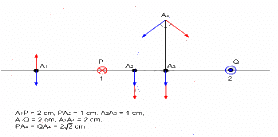
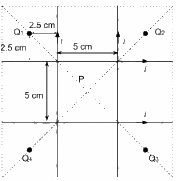
Q.12. Four long, straight wires, each carrying a current of 5.0 A, are placed in a plane as shown in figure. The points of intersection form a square of side 5.0 cm.
(a) Find the magnetic field at the centre P of the square.
(b) Q1, Q2, Q3, and Q4, are points situated on the diagonals of the square and at a distance from P that is equal to the diagonal of the square. Find the magnetic fields at these points.
Given:
Let the horizontal wires placed at the bottom and top are denoted as W1 and W2 respectively.
Let the vertical wires placed at the right and left to point P are denoted as W3 and W4 respectively.
Magnitude of current, I = 5 A
(a) Consider point P.
Magnetic fields due to wires W1 and W2 are the same in magnitude, but they are opposite in direction.
Magnetic fields due to wires W3 and W4 are the same in magnitude, but they are opposite in direction.
Hence, the net magnetic field is zero.
Net magnetic field at P due to these four wires = 0
(b) Consider point Q1.
Due to wire W1, separation of point Q1 from the wire (d) is 7.5 cm.
So, the magnetic field due to current in the wire is given by
= 4 × 10−5 T (In upward direction)
Due to wire W2, separation of point Q1 from the wire (d) is 2.5 cm.
So, the magnetic field due to current in the wire is given by(In upward direction)
Due to wire W3, separation of point Q1 from the wire (d) is 7.5 cm.
So, the magnetic field due to current in the wire is given by
BW3 = 4 × 10−5 T (In upward direction)
Due to wire W4, separation of point Q1 from the wire (d) is 2.5 cm.
So, the magnetic field due to current in the wire is given by(In upward direction)
∴ Net magnetic field at point Q1
At point Q2,
Magnetic field due to wire W1:
BW1 = 4 × 10−5 T (In upward direction)
Magnetic field due to wire W2:
Magnetic field due to wire W3:
Magnetic field due to wire W4:
∴ Net magnetic field at point Q2,
Similarly, at point Q3, the magnetic field is 1.1 × 10−4 T (in downward direction) and at point Q4, the magnetic field is zero.
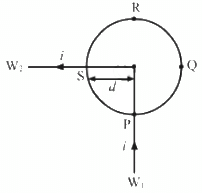
Q.13. Figure shows a long wire bent at the middle to form a right angle. Show that the magnitudes of the magnetic fields at the point P, Q, R and S are equal and find this magnitude.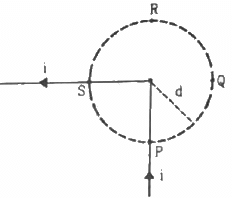
As shown in the figure, points P, Q, R and S lie on a circle of radius d.
Let the wires be named W1 and W2.
Now,
At point P, the magnetic field due to wire W1 is given by
B1 = 0
At point P, the magnetic field due to wire W2 is given by(Perpendicular to the plane in outward direction)
(Perpendicular to the plane in outward direction)
At point Q, the magnetic field due to wire W1 is given by(Perpendicular to the plane in inward direction)
At point Q, the magnetic field due to wire W2 is given by
B2 = 0(Perpendicular to the plane in inward direction)
At point R, the magnetic field due to wire W1 is given by
B1 = 0
At point R, the magnetic field due to wire W2 is given by
(Perpendicular to the plane in inward direction)
(Perpendicular to the plane in inward direction)
At point S, the magnetic field due to wire W1 is given by(Perpendicular to the plane in outward direction)
At point S, the magnetic field due to wire W2 is given by
B2 = 0(Perpendicular to the plane in outward direction)
Hence, the magnitude of the magnetic field at points P, Q, R and S is.
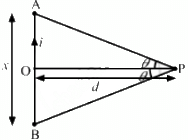
Q.14. Consider a straight piece of length x of a wire carrying a current i. Let P be a point on the perpendicular bisector of the piece, situated at a distance d from its middle point. Show that for d >> x, the magnetic field at P varies as 1/d2 whereas for d << x, it varies as 1/d.
Let AB be the wire of length x with midpoint O.
Given:
Magnitude of current = i
Separation of the point from the wire = d
Now,
The magnetic field on a perpendicular bisector is given by
And, if d < < x (neglecting d), then
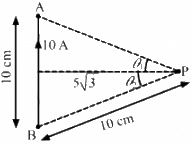
Q.15. Consider a 10-cm long piece of a wire which carries a current of 10 A. Find the magnitude of the magnetic field due to the piece at a point which makes an equilateral triangle with the ends of the piece.
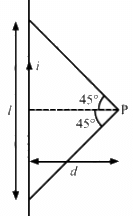
Let AB be the wire of length 10 cm and P be the required point.
Given:
Magnitude of current, i = 10 A
The angles made by points A and B with point P are
∴ Separation of the point from the wire, d =
Thus, the magnetic field due to current in the wire is given by
Q.16. A long, straight wire carries a current i. Let B1 be the magnetic field at a point P at a distance d from the wire. Consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the section B2 be the magnetic field at this point due to this second only. Find the value of d/l so that B2 differs from B1 by 1%.
Given:
Magnitude of current = i
Separation of the point from the wire = d
Thus, the magnetic field due to current in the long wire is given by
Also, the magnetic field due to a section of length l on a perpendicular bisector is given by
Now,
B1 > B2
According to the question,
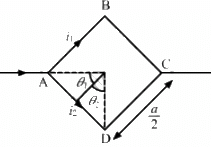
Q.17. Figure shows a square loop ABCD with edge-length a. The resistance of the wire ABC is r and that of ADC is 2r. Find the magnetic field B at the centre of the loop assuming uniform wires.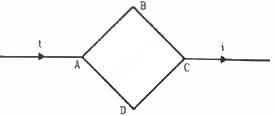
Let the currents in wires ABC and ADC be i1 and i2, respectively.
The resistances in wires ABC and ADC are r and 2r, respectively.
The angles made by points A and D with point O are
Separation of the point from the wire, d = a/2
Now,
The magnetic field due to current in wire AD is given by
The magnetic field at centre due to wire ADC is given by
(Perpendicular to the plane in outward direction)
The magnetic field at centre due to wire ABC is given by
(Perpendicular to the plane in inward direction)
(Perpendicular to the plane in inward direction)
Q.18. Figure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.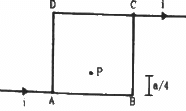
Q.19. Consider the situation described in the previous problem. Suppose the current i enters the loop at the points A and leaves it at the point B. Find the magnetic field at the centre of the loop.
The loop ABCD can be considered as a circuit with two resistances in parallel, one along branch AB and other along branch ADC.
As, the sides of the loop are identical, their resistances are also same.
Let the resistance of each side be r.
The resistance of branch AB = r
The resistance of branch ADC = 3r
The current in the branches are calculated as:
As current follow the least resistive path so
Current in branch AB = 3i/4
Current in branch ADC = i/4
At the centre of the loop:
Magnetic field due to wire AD, DC and CB will be into the plane of paper according to right hand thumb rule.
Magnetic field due to wire AB will be out of the plane of paper according to right hand thumb rule.
Net magnetic field at the centre = BAD +BDC +BCB − BAB which will be out of the plane of paper.
As, perpendicular distance of the centre from every wire will be equal to a/√2 and angle made by corner points of each side at the centre is 45º.
Q.20. The wire ABC shown in figure forms an equilateral triangle. Find the magnetic field B at the centre O of the triangle assuming the wire to be uniform.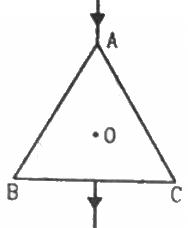
Let current 2I enter the circuit.
Since the wire is uniform, the current will be equally divided at point A (as shown in the figure).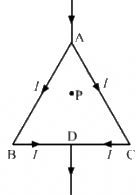
Now,
Magnetic field at P due to wire AB = B (say)
(Perpendicular to the plane in outward direction)
Magnetic field at P due to wire BD = B' (say)
(Perpendicular to the plane in outward direction)
Magnetic field at P due to wire AC = Magnetic field at P due to wire AB = B
(Perpendicular to the plane in inward direction)
Magnetic field at P due to wire CD = Magnetic field at P due to wire BD = B'
(Perpendicular to the plane in inward direction)
∴ Net magnetic field at P = B + B' − B − B' = 0
|
134 docs
|
FAQs on HC Verma Questions and Solutions: Chapter 35: Magnetic Field due to a Current- 2 - HC Verma Solutions - JEE
| 1. What is the magnetic field due to a current? |  |
| 2. How is the magnetic field due to a current calculated? |  |
| 3. What is the direction of the magnetic field due to a current? |  |
| 4. How does the magnetic field due to a current vary with distance? |  |
| 5. What is the relationship between the magnetic field due to a current and the current itself? |  |