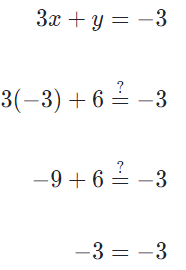Substitution Method | Mathematics for Digital SAT PDF Download

What is the substitution method?

Clear all your SAT doubts with EduRev Join for Free

Join for Free

Example 1: We're asked to solve this system of equations:
3x + y = −3
x = -y + 3

The second equation is solved for x, so we can substitute the expression −y + 3, in for x in the first  equation:
3x + y = −3
3(-y + 3) + y = -3
-3y + 9 + y = -3
-2y = -12
y = 6
Plugging this value back into one of our original equations, say  x = −y + 3x, we solve for the other variable:
x = -y + 3
x = -(6) + 3
x = -3
The solution to the system of equations is x = −3x, y = 6
We can check our work by plugging these numbers back into the original equations. Let's try  3x + y = −3

Yes, our solution checks out.

Example 2: We're asked to solve this system of equations:
7x + 10y = 36
-2x + y = 9

In order to use the substitution method, we'll need to solve for either x or y in one of the equations. Let's solve for y in the second equation:
-2x + y = 9
y = 2x + 9
Now we can substitute the expression 2x + 9 in for y in the first equation of our system:
7x + 10y = 36
7x + 10(2x + 9) = 36
7x + 20x + 90 = 36
27x + 90 = 36
3x + 10 =  4
3x = -6
x = -2
Plugging this value back into one of our original equations, say y = 2x + 9
we solve for the other variable:
y = 2x + 9
y = 2(-2) + 9
y = -4 + 9
y = 5
The solution to the system of equations is x = -2, y = 5