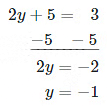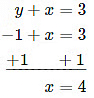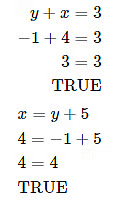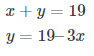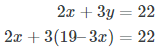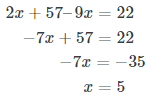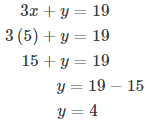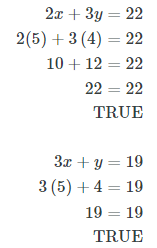Solved Examples: Substitution | Mathematics for Digital SAT PDF Download
Introduction
The substitution method is the algebraic method to solve simultaneous linear equations. As the word says, in this method, the value of one variable from one equation is substituted in the other equation. In this way, a pair of the linear equation gets transformed into one linear equation with only one variable, which can then easily be solved. Before moving to solve the linear equations using the substitution method, get an idea on what the algebraic method and graphical method is.- Algebraic Method: An Algebraic method is a collection of several methods, which are used to solve a pair of the linear equations that includes two variables. Generally, the algebraic method can be sub-divided into three categories: Substitution method Elimination method Cross-multiplication method
- Graphical Method: The graphical method is also known as the geometric method and is used to solve the system of linear equations. In this method, the equations are designed based on the objective function and constraints. To solve the system of linear equations, this method has undergone different steps to obtain the solutions.
In this article, we will focus mainly on solving the linear equations using the first algebraic method called “Substitution Method” in detail.
Solved Examples
Q1: Solve the equations using substitution method and find the values of a and b:
0.2a + 0.3b = 1.3
0.4a + 0.5b = 2.3.
Also, verify your answer.
Solution:
Given:
0.2a + 0.3b = 1.3 …(1)
0.4a + 0.5b = 2.3 … (2)
From equation (1), we get
0.2a = 1.3 – 0.3b
Hence, a = (1.3 – 0.3b)/0.2 …(3)
Substituting equation (3) in (2), we get
0.4[(1.3 – 0.3b)/0.2] + 0.5b = 2.3
0.4(1.3 – 0.3b) + 0.1b = 0.46
0.52 – 0.12b + 0.1b = 0.46
– 0.12b + 0.1b = 0.46 – 0.52
-0.02b = -0.06
Cancelling minus sign on both sides, we get
0.02b = 0.06
Hence, b = 3.
Now, substitute b = 3 in equation (1), we get
0.4a + 0.5(3) = 2.3
0.4a + 1.5 = 2.3
0.4a = 2.3 – 1.5
0.4a = 0.8
a = 0.8 /0.4
a = 2
Hence, a = 2 and b = 3 are the solutions of the equations 0.2a + 0.3b = 1.3 and 0.4a + 0.5b = 2.3.
Verification:
Substitute a = 2 and b = 3 in equation (1).
⇒ 0.2(2) + 0.3(3) = 1.3
⇒ 0.4 + 0.9 = 1.3
⇒ 1.3 = 1.3
Thus, LHS = RHS.
Hence, a = 2 and b = 3 are the solutions to the linear equation 0.2a + 0.3b = 1.3 and 0.4a + 0.5b = 2.3.
Q2: Find the values of x and y from the system of linear equations:
7p + 6q = 3800, and 3p + 5q = 1750
Solution:
p = 500, q = 50
Given linear equations:
7p + 6q = 3800 .. (1)
3p + 5q = 1750 …(2)
From (1), we can write:
7p = 3800 – 6q
⇒ p = (3800 – 6q)/7 …(3)
Substituting (3) in (2),
⇒ 3[(3800 – 6q)/7] + 5q = 1750
⇒ 11400 – 18q + 35q = 12250
⇒ -18q + 35q = 12250 – 11400
⇒ 17q = 850
⇒ q = 850/17
⇒ q = 50
Now, plug the value of q in equation (1), we get
7p + 6(50) = 3800
7p + 300 = 3800
7p = 3800 – 300
7p = 3500
p = 3500/7
p = 500
Hence, the values of p and q are 500 and 50, respectively.
Q3: Using substitution method, solve the following equations:
p + 3q = 13 and 3p + q = 7.
Also, justify your answer.
Solution:
Given equations:
p + 3q = 13 …(1)
3p + q = 7 …(2)
From equation (1), we can write
p = 13 – 3q ..(3)
Substituting (3) in (2), we get
⇒ 3(13 – 3q) + q = 7
⇒ 39 – 9q + q = 7
⇒ 39 – 8q = 7
⇒ -8q = 7 – 39
⇒ -8q = -32
⇒ 8q = 32
⇒ q = 32/8
⇒ q = 4
Now, substituting q = 4 in equation (1), we get
⇒ p + 3(4) = 13
⇒ p + 12 = 13
⇒ p = 13 – 12
⇒ p = 1
Hence, the solutions are:
p = 1 and q = 4
Verification:
Substitute p = 1 and q = 4 in equation (1),
⇒ 1 + 3(4) = 13
⇒ 1 + 12 = 13
⇒ 13 = 13
Thus, LHS = RHS.
Therefore, p = 1 and q = 4 are the solutions of the equations p + 3q = 13 and 3p + q = 7.
Q4: Solve the pair of linear equations given below using the substitution method:
3p – q = 3
9p – 3q = 9
Solution:
Given linear equations:
3p – q = 3 …(1)
9p – 3q = 9 …(2)
From (1), we can write
⇒ 3p = 3 + q
⇒ p = (3+q)/3 …(3)
Now, substitute (3) in (2), we get
⇒ 9[(3+q)/3] – 3q = 9
⇒ 9 +3q – 3q = 9
⇒ 9 = 9
Therefore, substituting different values of q in p = (3+q)/3, we get different p values.
Thus, the system of linear equations has infinitely many solutions.
Q5: Solve the equations 2p – 3q = 2 and p + 2q = 8, using the method of substitution.
Solution:
Given:
2p – 3q = 2 …(1)
p + 2q = 8 …(2)
Using the substitution method, we can find the values of p and q as given below:
From equation (1),
⇒ 2p = 2 + 3q
⇒ p = (2 + 3q)/2
Now, substituting p = (2 + 3q)/2 in (2), we get
⇒ [(2 + 3q)/2] + 2q = 8
⇒ 2 + 3q + 4q = 16
⇒ 2 + 7q = 16
⇒7q = 16 – 2
⇒ 7q = 14
⇒ q = 14/7 = 2
Putting q = 2 in equation (2),
p + 2(2) = 8
p + 4 = 8
p = 8 – 4
p = 4
Hence, the solution to the system of equations 2p – 3q = 2 and p + 2q = 8 are:
p = 4 and q = 2.
Q6: Solve for x and y.
Equation A: y + x = 3
Equation B: x = y + 5
Solution:
The goal of the substitution method is to rewrite one of the equations in terms of a single variable. Equation B tells us that x=y+5, so it makes sense to substitute y+5 into Equation A for x.y + x = 3
x = y + 5Substitute y + 5 into Equation A for x.
y + x = 3
y + (y + 5) = 3Simplify and solve the equation for y.
Now find x by substituting this value for y into either equation and solve for x. We will use Equation A here.
Finally, check the solution x=4, y=−1 by substituting these values into each of the original equations.
Ans: x = 4 and y = −1
The solution is (4,−1).
Q7: Solve the following system of equations by substitution.
−x + y = −5
2x − 5y = 1
Solution:
First, we will solve the first equation for y.−x + y = −5
y = x − 5Now, we can substitute the expression x − 5 for y in the second equation.
2x − 5y = 1
2x − 5(x − 5) = 1
2x − 5x + 25 = 1
−3x = −24
x = 8Now, we substitute x = 8 into the first equation and solve for y.
−(8) + y = −5
y = 3Our solution is (8, 3)(8, 3).
Check the solution by substituting (8, 3)(8, 3) into both equations.
−x + y = −5
−(8) + (3) = −5 True
2x − 5y = 1
2(8) − 5(3) = 1 TrueThe substitution method can be used to solve any linear system in two variables, but the method works best if one of the equations contains a coefficient of 1 or –1 so that we do not have to deal with fractions.
Q8: Solve for x and y.
2x + 3y = 22
3x + y = 19
Solution:
Choose an equation to use for the substitution. The second equation,
3x + y = 19, can easily be rewritten in terms of y, so it makes sense to start there.
2x + 3y = 22
3x + y = 19Rewrite 3x + y = 19 in terms of y.
Substitute 19 – 3x for y in the other equation.
Simplify and solve the equation for x.
Substitute x = 5 back into one of the original equations to solve for y.
Check both solutions by substituting them into each of the original equations.
Ans: x = 5 and y = 4
The solution is (5, 4)(5, 4).
Q9: Solve the system of linear equations using substitution method:
p + q = 14 and p – q = 2
Solution:
Given:
p + q = 14 …(1)
p – q = 2 … (2)
From equation (1),
p = 14 – q …(3)
Now, substitute (3) in (2), we get
(14 – q) – q = 2
14 – 2q = 2
-2q = 2 – 14
-2q = -12
q = -12/-2
q = 6
Now, substitute q = 6 in (1)
p + 6 = 14
p = 14 – 6
p = 8
Hence, the solutions are: p = 8 and q = 6.
Q10: Solve the linear equations using the substitution method:
11p + 15q = -23
7p – 2q = 20
Solution:
Given system of linear equations are:
11p + 15q = -23 …(1)
7p – 2q = 20 …(2)
From equation (1), we can write the following:
⇒ 11p = -23 – 15q
⇒ 11p = – (23 + 15q)
⇒ p = – (23 + 15q)/11 …(3)
Now, substitute equation (3) in (2)
⇒ 7[- (23 + 15q)/11] – 2q = 20
⇒ -(161 + 105q) – 22q = 220
⇒ -161 – 105q – 22q = 220
⇒ -105q – 22q = 220 + 161
⇒ – 127q = 381
⇒ q = -381/127
⇒ q = -3
Substituting q = -3 in (2),
⇒ 7p – 2(-3) = 20
⇒ 7p + 6 = 20
⇒ 7p = 20 – 6
⇒ 7p = 14
⇒ p = 14/7
⇒ p = 2
Therefore, the values of p and q are 2 and -3, respectively.
|
185 videos|124 docs|75 tests
|