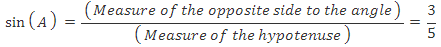Sine, Cosine and Tangent Basics | Mathematics for Digital SAT PDF Download

Trigonometric Formulas: Sine, Cosine, Tangent

Although trigonometry makes up less than 5% of all math questions, you still want to get those questions right, and you won't be able to answer any trigonometry questions correctly without knowing the following formulas: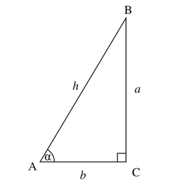Find the sine of an angle given the measures of the sides of the triangle.

In the figure above, the sine of the labeled angle would be a / h
Find the cosine of an angle given the measures of the sides of the triangle.
In the figure above, the cosine of the labeled angle would be b / h
Find the tangent of an angle given the measures of the sides of the triangle.
In the figure above, the tangent of the labeled angle would be a / b
A helpful memory trick is an acronym: SOHCAHTOA.
You should also know the complementary angle relationship for sine and cosine, which is .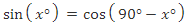

How to Apply Trigonometry Skills on SAT Math

There are two main trigonometry questions types you'll see on the test. I'll teach you how to address each.
Question type 1 will ask you to find the sine, cosine, or tangent and using the measures of the sides of the triangle. In order to answer these questions, you will need to use a diagram (that means drawing one if it's not given to you).
Let's walk through this example:
Triangle ABC is a right triangle where angle B measures 90°; the hypotenuse is 5 and side AB is 4. What is cosine A?

First, set up this triangle using the given information:
Then, identify the information you need. In this case, the question asked for the cosine A. We know, based on the previous formulas that .  Identify the pieces you need: the angle, the adjacent side to the angle, and the hypotenuse:
We have all the information we need, so we just need to put it into the formula:
4/5 is the answer.

A slightly harder version of this question might ask you for sine A instead of cosine A. If you look back at the diagram, you'll notice we don't know what the measure of the opposite side to angle A is (which is what we need to find sine A).In that case, we need to use the Pythagorean theorem (or our knowledge of 3-4-5 right triangles) to find the measure of the opposite side to angle A (BC).
Know that we know that side BC is 3, we just need to put it into the formula:

Question type 2 will ask you to find the sine, cosine, or tangent of an angle using a different given sine, cosine, or tangent of an angle. Similarly to question type one, to answer these questions, you'll need to use a diagram (that means drawing one if it's not given to you).
Check out this example: In a right ABC triangle, where B is the right angle, cos(A) = 4/5. What is the sin(C)?

You want to attack these problems by drawing a diagram, but first you need to figure out what should go where. Use the cosine formula to figure out how to draw the diagram.
Measure of adjacent side (AB) = 4
Measure of the hypotenuse (AC) = 5
You may notice it's the same triangle from the previous example. In this case, we want to find cosine C. We know, based on the previous formulas that . Identify the pieces you need: the angle, the adjacent side to the angle, and the hypotenuse.
4/5 is the Answer.

A slightly harder version of this question might ask you for tangent C instead of sine C. If you look back at the diagram, you'll notice we don't know what the measure of the adjacent side to angle C is (which is what we need to find tan A).

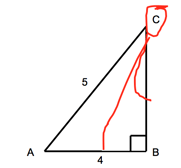In that case, we need to use the Pythagorean theorem (or our knowledge of 3-4-5 right triangles) to find the measure of the adjacent side to angle C (BC).
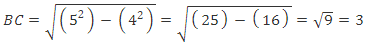Know that we know that side BC is 3, we just need to put it into the formula:
Now that we know how to apply the necessary formulas to tackle trig questions.