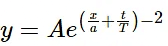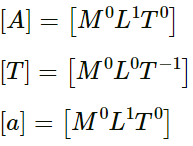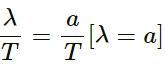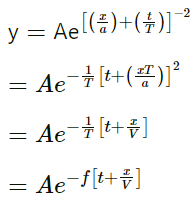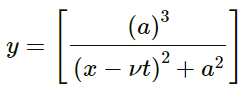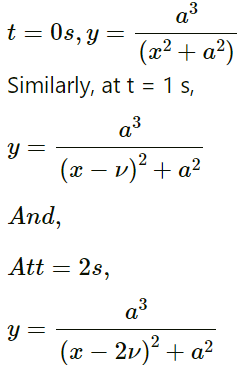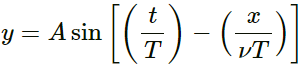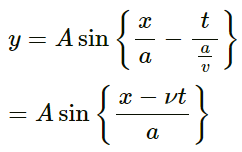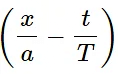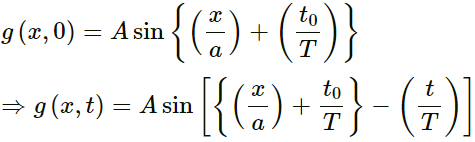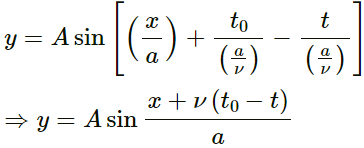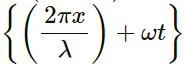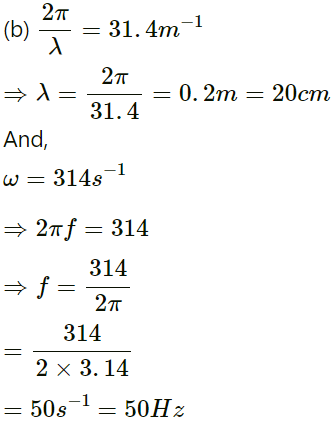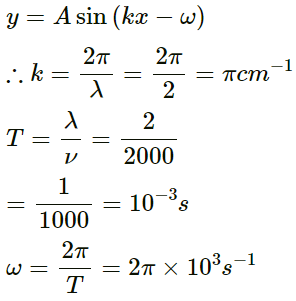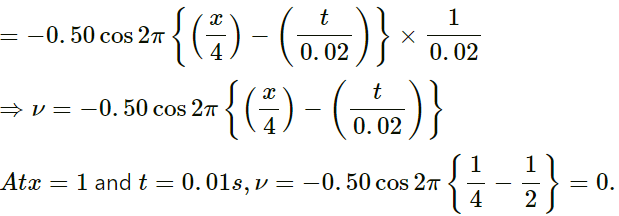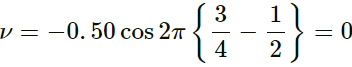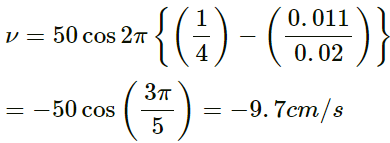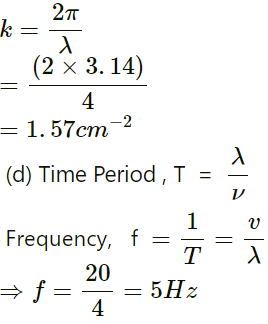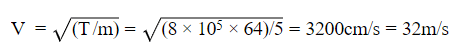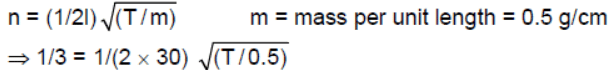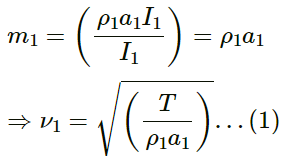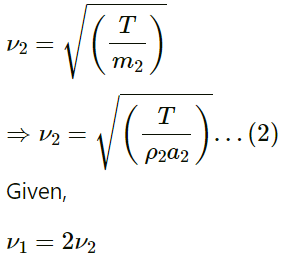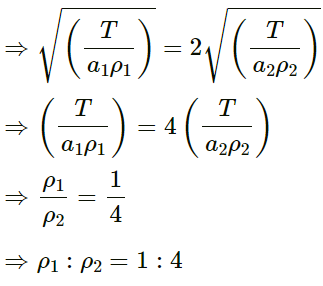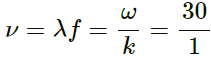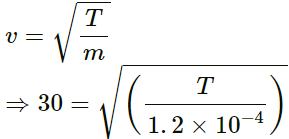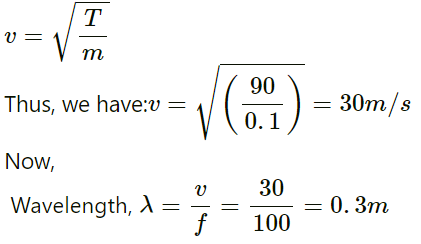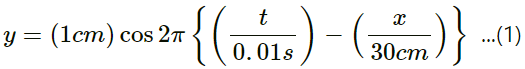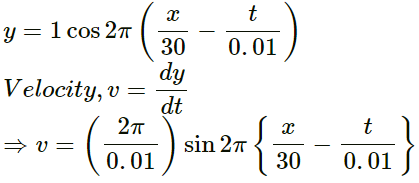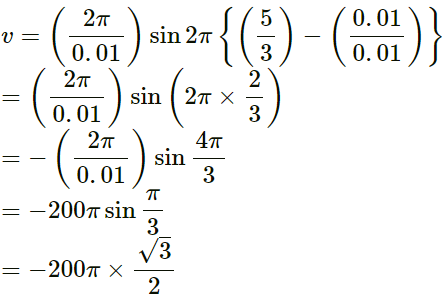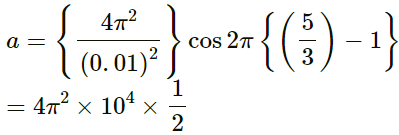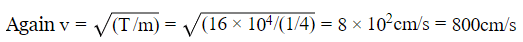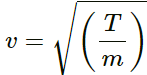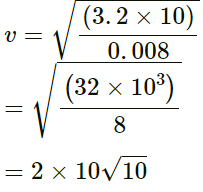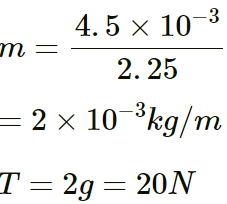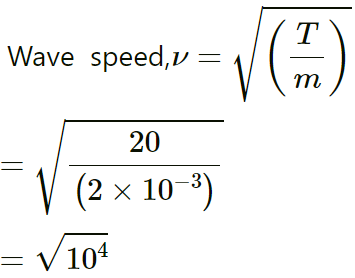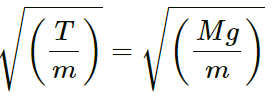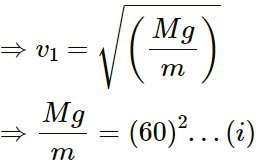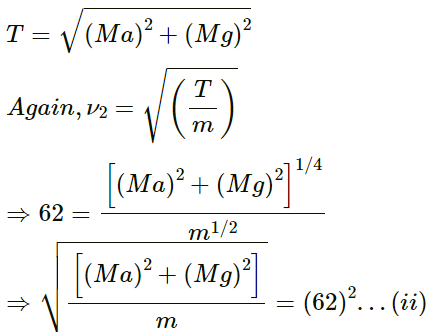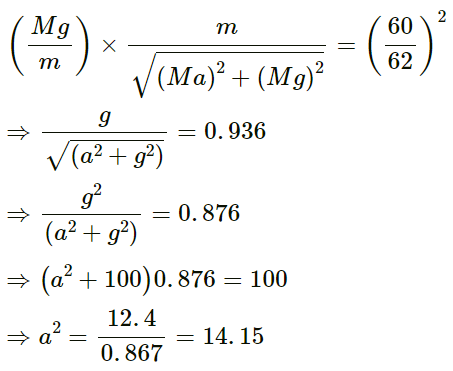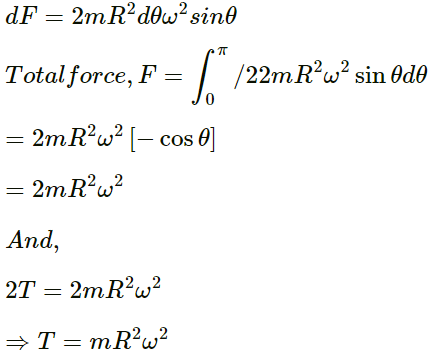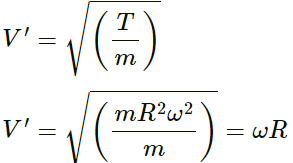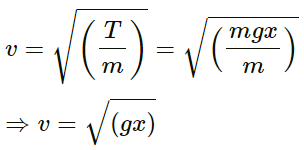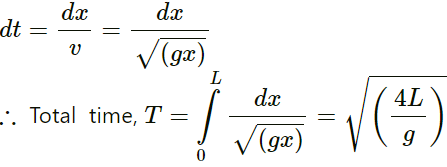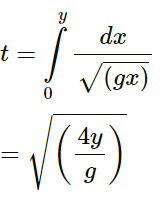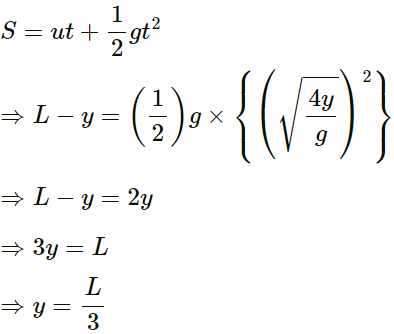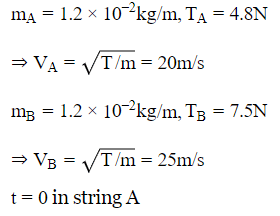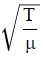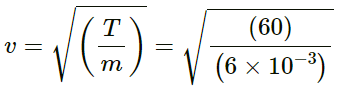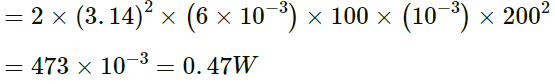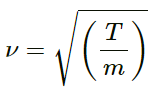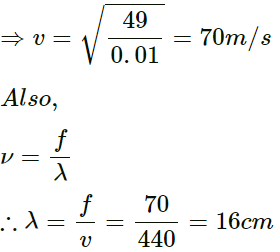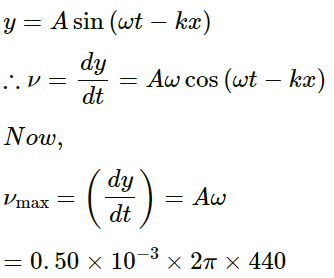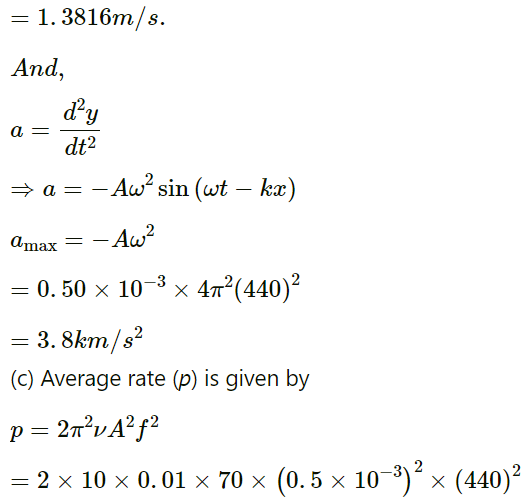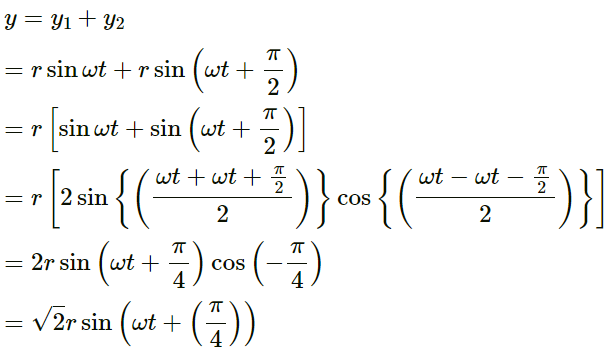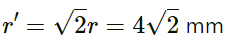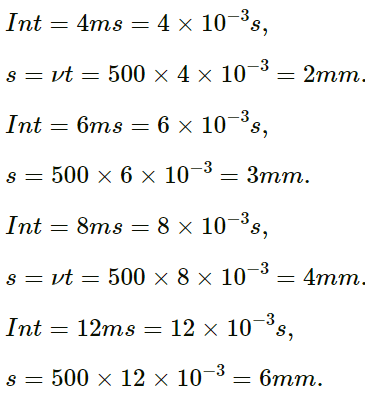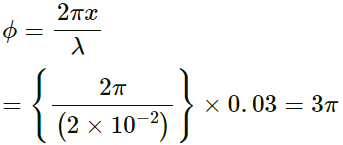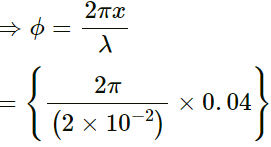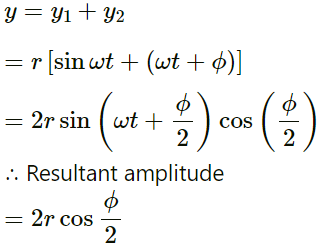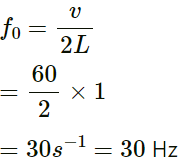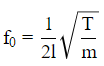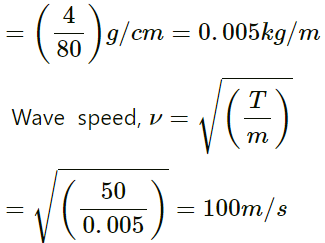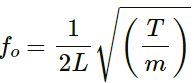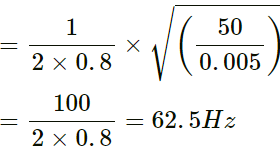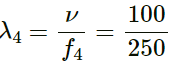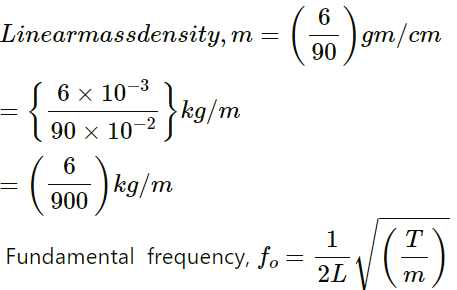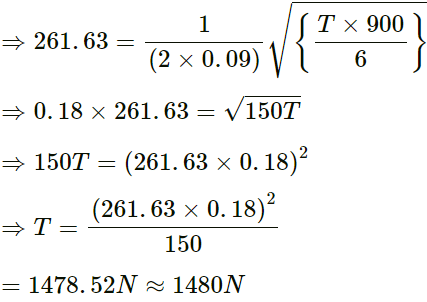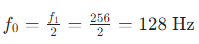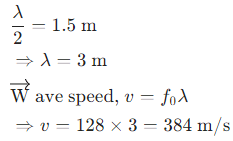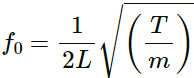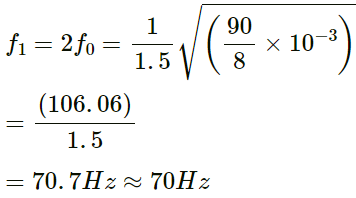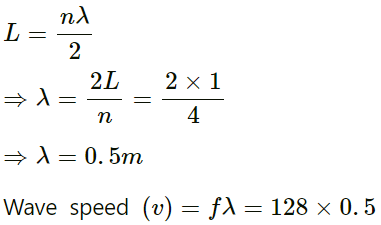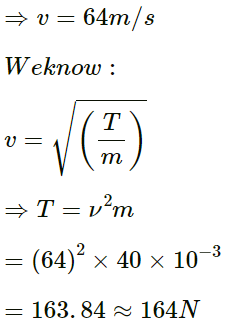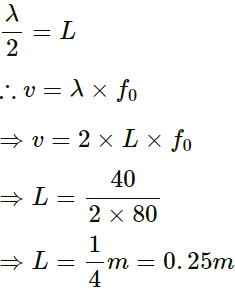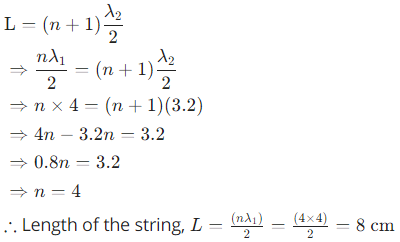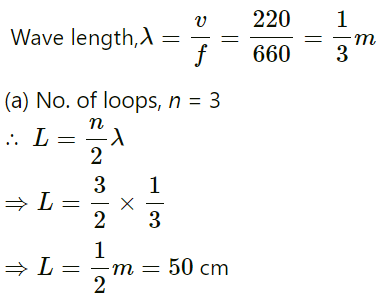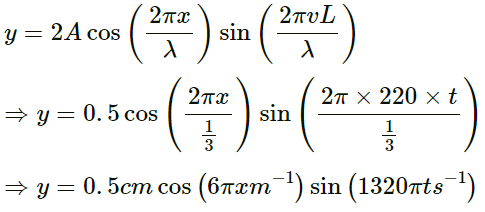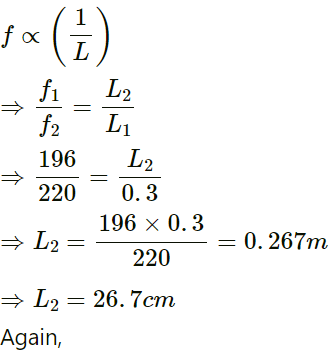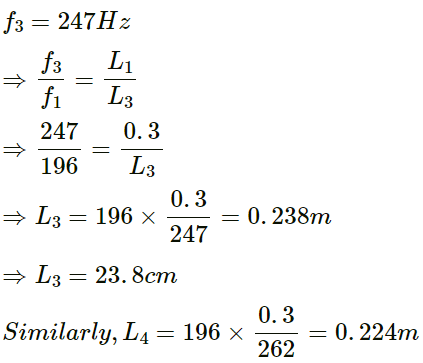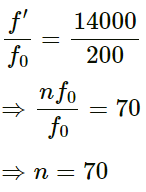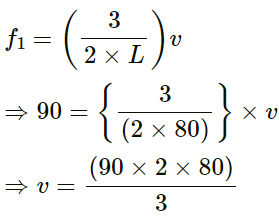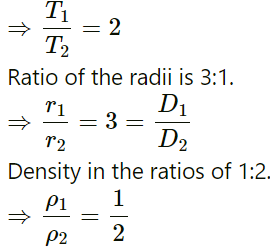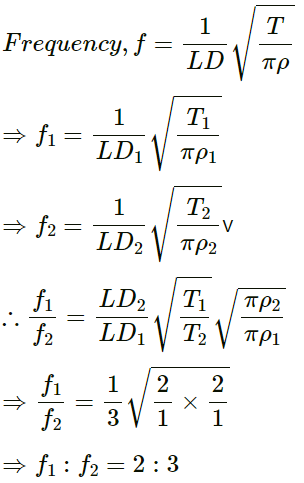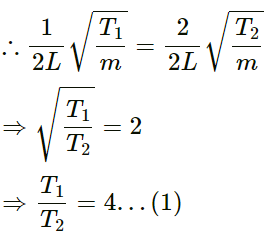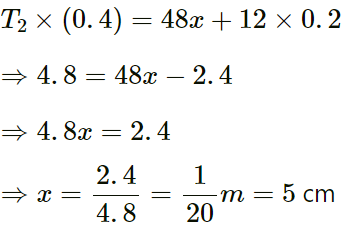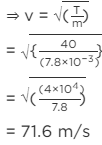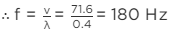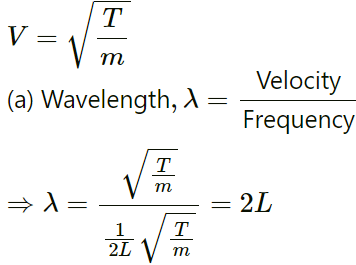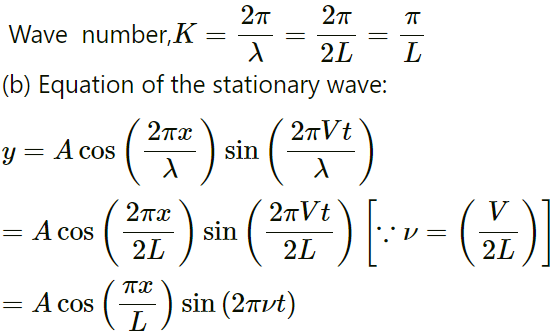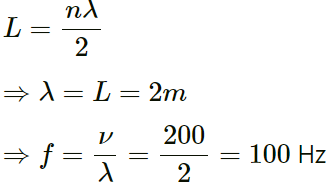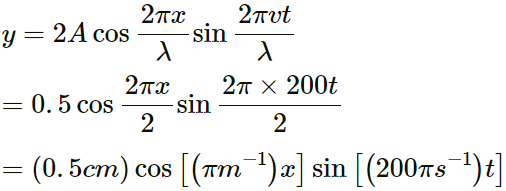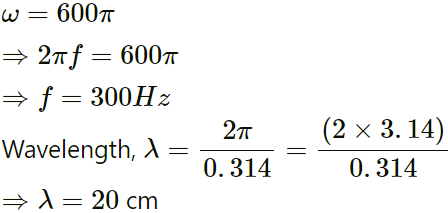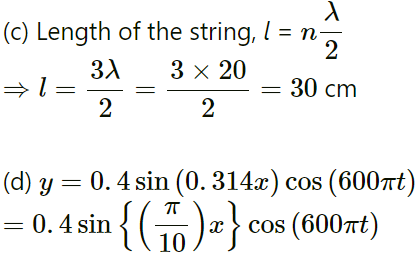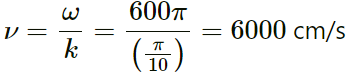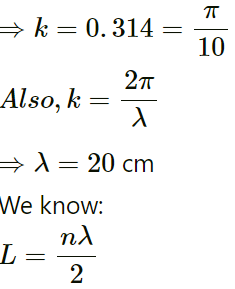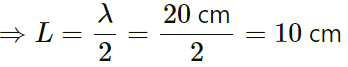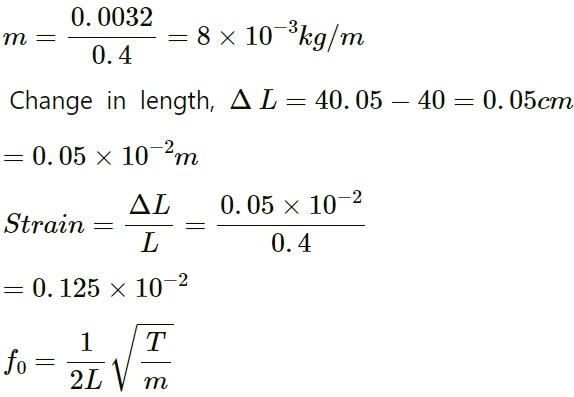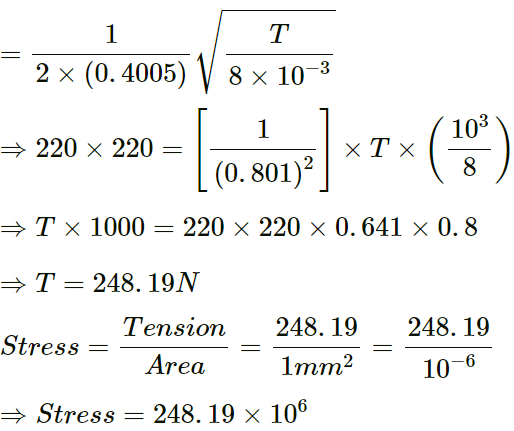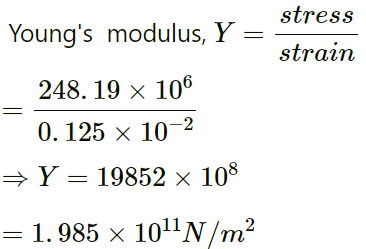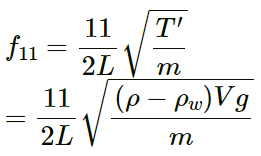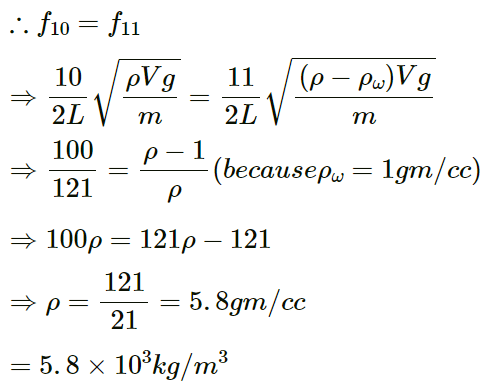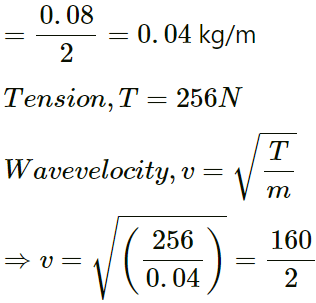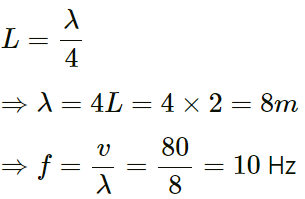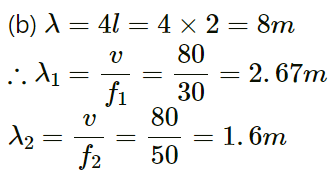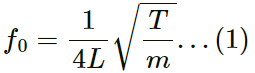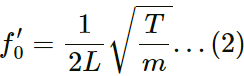HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 2 | HC Verma Solutions - JEE PDF Download
Exercise
Q.1. A wave pulse passing on a string with a speed of 40 cm s−1 in the negative x-direction has its maximum at x = 0 at t = 0. Where will this maximum be located at t = 5 s?
Given,
Speed of the wave pulse passing on a string in the negative x-direction = 40 cms−1
As the speed of the wave is constant, the location of the maximum after 5 s will be
s = v × t
= 40 × 5
= 200 cm (along the negative x-axis)
Therefore, the required maximum will be located after x = −2 m.
Q.2. The equation of a wave travelling on a string stretched along the X-axis is given by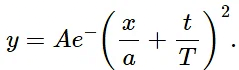
(a) Write the dimensions of A, a and T.
(b) Find the wave speed.
(c) In which direction is the wave travelling? (d) Where is the maximum of the pulse located at t = T? At t = 2 T?
Given,
Equation of the wave travelling on a string stretched along the X-axis:
(a) The dimensions of A (amplitude), T (time period) and α = λ/2π, which will have the dimensions of the wavelength, are as follows:
(b) Wave speed, v =
(c) If y =, then the wave travels in the negative direction; and if y =
, then the wave travels in the positive direction.
Thus, we have:
Hence, the wave is travelling is the negative direction.
(d) Wave speed, v = α/t Maximum pulse at t = T = (α/t) x T = α (Along the negative x - axis)
Maximum pulse at t = 2T =(Along the negative x - axis)
Therefore, the wave is travelling in the negative x-direction.
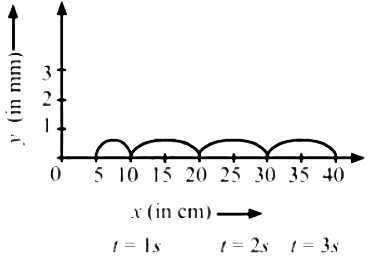
Q.3. Following Figure shows a wave pulse at t = 0. The pulse moves to the right with a speed of 10 cm s−1. Sketch the shape of the string at t = 1 s, 2 s and 3 s.

Given,
Wave pulse at t = 0Wave speed = 10 cms−1
Using the formula
s = v x t
At:
t = 1s, s1 = v x t = 10 x 1 = 10cm
t = 1s, s2 = v x t = 10 x 1 = 20cm
t = 1s, s3 = v x t = 10 x 1 = 30cm
Q.4. A pulse travelling on a string is represented by the function y = 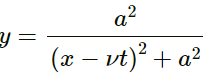 , where a = 5 mm and ν = 20 cm-1. Sketch the shape of the string at t = 0, 1 s and 2 s. Take x = 0 in the middle of the string.
, where a = 5 mm and ν = 20 cm-1. Sketch the shape of the string at t = 0, 1 s and 2 s. Take x = 0 in the middle of the string.
Given,
Pulse travelling on a string,
α = 5mm = 0.5cm
Wave speed, v = 20cm/s
So, at
To sketch the shape of the string, we have to plot a graph between y and x at different values of t.
Q.5. The displacement of the particle at x = 0 of a stretched string carrying a wave in the positive x-direction is given f(t) = A sin (t/T). The wave speed is v. Write the wave equation.
Given,
Equation of the wave travelling in the positive x-direction at x = 0:
f(t) = A sin (t/T)
Here,
Wave speed = v
Wavelength, λ = vT
T = Time period
Therefore, the general equation of the wave can be represented by
Q.6. A wave pulse is travelling on a string with a speed v towards the positive X-axis. The shape of the string at t = 0 is given by g(x) = Asin(x/α), where A and a are constants.
(a) What are the dimensions of A and α ?
(b) Write the equation of the wave for a general time t, if the wave speed is v.
The shape of the string at t = 0 is given by g(x) = A sin(x/α), where A and α are constants.
Dimensions of A and α are governed by the dimensional homogeneity of the equation g(x) = A sin(x/α).
Now,(a) [M0L1T0] = [A]
⇒ [A] = [L]
And,
[α] = [M0L1T0]
⇒ [α] = [L](b) Wave speed = v
∴ Time period, T = α/v
Here,
a = Wave length = λ
The general equation of wave is represented by
Q.7. A wave propagates on a string in the positive x-direction at a velocity v t = t0 is given by g(x, t0) = A sin (x/α) . Write the wave equation for a general time t.
Given,
Wave velocity = v
Shape of the string at
t = t0
g(x, t0) = A sin (x/α)
For a wave travelling in the positive x-direction, the general equation is given by y = A sin
Putting t = − t and comparing with equation (i), we get:
Now,
T = α/v
Here,
a = Wave length
nu = Velocity of the wave
Thus, we have:
Q.8. The equation of a wave travelling on a string is y = (0.10mm) sin [(31.4m-1)x + (314s-1) t)]
(a) In which direction does the wave travel?
(b) Find the wave speed, the wavelength and the frequency of the wave.
(c) What is the maximum displacement and the maximum speed of a portion of the string?
Given,
Equation of the wave,
y = (0.10mm) sin [(31.4m-1)x + (314s-1) t)]
The general equation is y = A sin
From the above equation, we can conclude:
(a) The wave is travelling in the negative x-direction.
Wave speed:
v = λf = 20 x 50
= 1000cm/s
(c) Maximum displacement, A = 0.10 mm
Maximum velocity = aω = 0.1 x 10-1 x 314
= 3.14 cm/s
Q.9. A wave travels along the positive x-direction with a speed of 20 m s−1. The amplitude of the wave is 0⋅20 cm and the wavelength 2⋅0 cm.
(a) Write the suitable wave equation which describes this wave.
(b) What is the displacement and velocity of the particle at x= 2⋅0 cm at time t = 0 according to the wave equation written?
Can you get different values of this quantity if the wave equation is written in a different fashion?
A wave travels along the positive x-direction.
Wave amplitude (A) = 0.20 cm
Wavelength (λ) = 20 cm
Wave speed (v) = 20 m/s
(a) General wave equation along the x-axis:Wave equation:
y = (0.2cm) sin [πcm-1) x - (2π x 10-3s-1)]
(b) As per the question
For the wave equation ,we need to find the displacement and velocity at x = 2 cm and t = 0.
y = (0.2) cm sin 2π = 0
∴ v = Aωcos πx
= 0.2 x 2000π x cos 2π
= 400π
= 400πcm/s = 4πm/sIf the wave equation is written in a different fashion, then also we will get the same values for these quantities.
Q.10. A wave is described by the equation y = (1 . 0mm) sin π 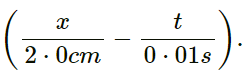
(a) Find the time period and the wavelength?
(b) Write the equation for the velocity of the particles. Find the speed of the particle at x = 1⋅0 cm at time t = 0⋅01 s.
(c) What are the speeds of the particles at x = 3⋅0 cm, 5⋅0 cm and 7⋅0 cm at t = 0⋅01 s?
(d) What are the speeds of the particles at x = 1⋅0 cm at t = 0⋅011, 0⋅012, and 0⋅013 s?
The wave equation is represented by y = (1 . 0mm) sin π
Let:
Time period = T
Wavelength = λ
(a) T = 2 x 0.01 = 0.02s = 20ms
λ = 2 x 2 = 4cm
(b) Equation for the velocity of the particle:(c) (i) Speed of the particle:
Atx = 3cm and t = 0.01s(ii) at x = 5cm and t = 0.01s,
v = 0
(iii) Atx = 7cm and t = 0.1 s, v = 0
(iv) Atx = 1cm and t = 0.11s
(By changing the value of t, the other two can be calculated.)
Q.11. A particle on a stretched string supporting a travelling wave, takes 5⋅0 ms to move from its mean position to the extreme position. The distance between two consecutive particles, which are at their mean positions, is 2⋅0 cm. Find the frequency, the wavelength and the wave speed.
Time period, T = 4 × 5 ms
= 20 × 10−3 = 2 × 10−2s
λ = 2 × 2 cm = 4 cm
Frequency, f = 1/T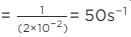
= 50 H z
Wave speed, λ f = 4 × 10−2 × 50 m/s
= 200 × 10−2 m/s = 2 m/s
Q.12. Figure shows a plot of the transverse displacements of the particles of a string at t = 0 through which a travelling wave is passing in the positive x-direction. The wave speed is 20 cm s−1. Find (a) the amplitude, (b) the wavelength, (c) the wave number and (d) the frequency of the wave.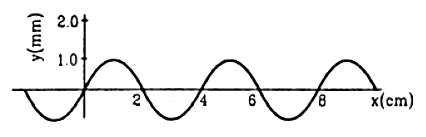
Given:
Wave speed,
ν = 20 cm/s
From the graph, we can infer:
(a) Amplitude, A = 1 mm
(b) Wavelength, λ = 4 cm
(c) Wave number,
Q.13. A wave travelling on a string at a speed of 10 m s−1 causes each particle of the string to oscillate with a time period of 20 ms.
(a) What is the wavelength of the wave?
(b) If the displacement of a particle of 1⋅5 mm at a certain instant, what will be the displacement of a particle 10 cm away from it at the same instant?
Given, Wave speed (v) = 10 ms−1
Time period (T) = 20 ms
= 20 × 10−3 = 2 × 10−2s
(a) Wavelength of the wave:
λ = vt = 10 × 2 × 10−2
= 0 . 02m = 20cm
(b) Displacement of the particle at a certain instant:
y = α sin (wt − kx)
⇒ 1 . 5 = α sin (wt − kx)
Phase difference of the particle at a distance x = 10 cm:The Displacement is given by
y' = α sin (wt − kx + π)
= α sin (wt − kx) = 1.5mm
∴ Displacement = 1.5 mm
Q.14. A steel wire of length 64 cm weighs 5 g. If it is stretched by a force of 8 N, what would be the speed of a transverse wave passing on it?
Mass = 5g
Length = 64cm
∴ Mass per unit length = 5/64 g/cm
∴Tension, T = 8N = 8 × 105 dyne
Q.15. A string of length 20 cm and linear mass density 0⋅40 g cm−1 is fixed at both ends and is kept under a tension of 16 N. A wave pulse is produced at t = 0 near an ends as shown in the figure, which travels towards the other end.
(a) When will the string have the shape shown in the figure again?
(b) Sketch the shape of the string at a time half of that found in part (a).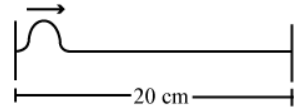
Velocity of the wave,
Time taken to reach to the other end = 20/2000 = 0.01 sec
Time taken to see the pulse again in the original position = 0.01x2 = 0.02 sec
b) At t = 0.01 s, there will be a ‘though’ at the right end as it is reflected.
Q.16. A string of linear mass density 0⋅5 g cm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end (See figure). The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20 cm s−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring.
(a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to region its shape.
(b) The shape of the string changes periodically with time. Find this time period.
(c) What is the tension in the string?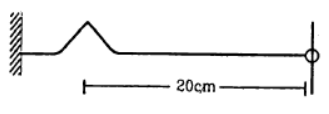
The crest reflects as a crest here, as the wire is traveling from denser to rarer medium.
⇒ phase change = 0
(a) To again original shape distance travelled by the wave S = 20+20 = 40 cm.
Wave speed, v = 20m/s =>time = s/v = 40/20 = 2 sec
(b) The wave regains its shape, after traveling a periodic distance = 2x30 = 60cm
Time period =60/20 =3 sec.
∴ Time period = 60/20 = 3 sec.
(c) Frequency, n = (1/3 sec-1)
⇒ T = 400 x 0.5 = 200 dyne = 2 x 10-3 Newton.
Q.17. Two wires of different densities but same area of cross section are soldered together at one end and are stretched to a tension T. The velocity of a transverse wave in the first wire is double of that in the second wire. Find the ratio of the density of the first wire to that of the second wire.
Let:
m = Mass per unit length of the first wire
a = Area of the cross section
ρ = Density of the wire
T = Tension
Let the velocity of the first string be v1.
Thus, we have:
The mass per unit length can be given as
Let the velocity of the first string be v2.
Thus, we have:
Q.18. A transverse wave described by y = ( 0 ⋅ 02m) sin (1 ⋅ 0m−1) x + (30s− 1)t propagates on a stretched string having a linear mass density of 1 ⋅ 2 × 10−4 kgm−1 the tension in the string.
Given,
Wave equation,
y = (0.02m) sin (1.0.m-1) x + (30s-1)t
Let:
Mass per unit length, m = 1 . 2 \times {10}^{- 4} kg/m
From the wave equation, we have:
Velocity of the wave in the stretched string is given by
⇒ v = 30m/s
We know:
⇒ T = 108 x 10-3 = 0.108 N
So, the tension in the string is 0.108 N.
Q.19. A traveling wave is produced on a long horizontal string by vibrating an end up and down sinusoidally. The amplitude of vibration is 1⋅0 and the displacement becomes zero 200 times per second. The linear mass density of the string is 0⋅10 kg m−1 and it is kept under a tension of 90 N.
(a) Find the speed and the wavelength of the wave.
(b) Assume that the wave moves in the positive x-direction and at t = 0, the end x = 0 is at its positive extreme position. Write the wave equation.
(c) Find the velocity and acceleration of the particle at x = 50 cm at time t = 10 ms.
Given,
Amplitude of the wave = 1 cm
Frequency of the wave,
f = 200/2 = 100 Hz
Mass per unit length, m = 0.1 kg/m
Applied tension, T = 90 N
(a) Velocity of the wave is given by
⇒ λ = 30 cm(b) At x = 0, displacement is maximum.
Thus, the wave equation is given by
(c) Using cos (-θ) = cos θ
in equation (1), we get:
And,
Acceleration,
When x = 50 cm, t = 10 ms = 10 \times {10}^{- 3} s .
Now,
In magnitude, v = 5.4 m/s.
Similarly,
= 2 x 105cm/s2 or 2 km/s2
Q.20. A string of length 40 cm and weighing 10 g is attached to a spring at one end and to a fixed wall at the other end. The spring has a spring constant of 160 N m−1 and is stretched by 1⋅0 cm. If a wave pulse is produced on the string near the wall, how much time will it take to reach the spring?
Given:
l = 40cm,mass = 10g
∴ mass per unit length, m=10/40 = 1/4(g/cm)
spring constant K=160N/m
deflection = x = 1cm = 0.01m
⇒ T = kx=160 x 0.01 = 1.6N = 16 × 104 dyne
∴ Time taken by the pulse to reach the spring
t = 40/800 = 1/20 = 0/05sec.
Q.21. Two blocks each having a mass of 3⋅2 kg are connected by a wire CD and the system is suspended from the ceiling by another wire AB (See following figure). The linear mass density of the wire AB is 10 g m−1 and that of CD is 8 g m−1. Find the speed of a transverse wave pulse produced in AB and CD.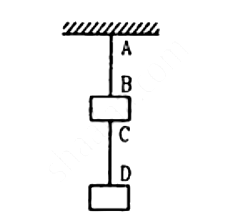
Given,
m1 = m2 = 3.2kgLinear mass density of wire AB = 10 gm−1 = 0.01 kgm−1
Linear mass density of wire CD = 8 gm−1 = 0.008 kgm−1
For string CD, velocity is defined as
Here, T is the tension and m is the mass per unit length.
For string CD,
T = 3.2 x g
Thus, we have:
= 20 x 3.14 ≈ 63s
For string AB,
T = 2 x 3.2g = 64N
Thus, we have:
= 80 m/s
Q.22. In the arrangement shown in figure, the string has a mass of 4⋅5 g. How much time will it take for a transverse disturbance produced at the floor to reach the pulley? Take g = 10 m s−2.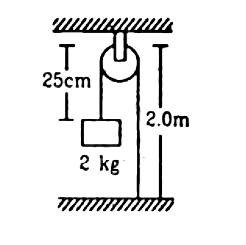
Given,
Mass of the block = 2 kg
Total length of the string = 2 + 0.25 = 2.25 m
Mass per unit length of the string:
= 102 m/s = 100 m/sTime taken by the disturbance to reach the pulley:
t = (s/v)
= 2/100 = 0.2s
Q.23. A 4⋅0 kg block is suspended from the ceiling of an elevator through a string having a linear mass density of 19 ⋅ 2 × 10−3kgm−1 . Find the speed (with respect to the string) with which a wave pulse can proceed on the string if the elevator accelerates up at the rate of 2⋅0 m s−2. Take g = 10 m s−2.
m = 19.2x10–3 kg/m
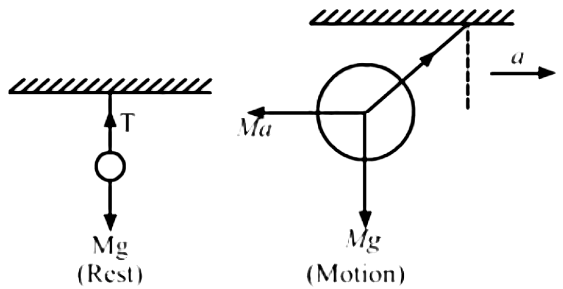
from the freebody diagram
T - 4g - 4a = 0
⇒ T = 4(a + g) = 48N
wave speed, v = √(T/m) = 50m/s
Q.24. A heavy ball is suspended from the ceiling of a motor car through a light string. A transverse pulse travels at a speed of 60 cm s−1 on the string when the car is at rest and 62 cm s−1 when the car accelerates on a horizontal road. Find the acceleration of the car. Take g = 10 m s−2
Given,
Speed of the transverse pulse when the car is at rest, v1 = 60 cm s−1
Speed of the transverse pulse when the car accelerates, v2 = 62 cm s−1
Let:
Mass of the heavy ball suspended from the ceiling = M
Mass per unit length = m
Now,
Wave speed, v =
When car is at rest:
Tension in the string, T = Mg
When car is having acceleration:
Tension,
From equations (i) and (ii), we get:
⇒ α = 3.76m/s2
Therefore, acceleration of the car is 3 . 76 m/s2 .
Q.25. A circular loop of string rotates about its axis on a frictionless horizontal place at a uniform rate so that the tangential speed of any particle of the string is ν. If a small transverse disturbance is produced at a point of the loop, with what speed (relative to the string) will this disturbance travel on the string?
Let,
V = Linear velocity of the string
m = Mass per unit length of the the string.
R = Radius of the loop
ω = Angular velocityConsider one half of the string, as shown in the figure.
The half loop experiences centrifugal force at every point (away from the centre) balanced by tension 2T.
Consider an element of angular part dθ at angle θ.
So,
Length of the element
= Rdθ, mass = mRdθ
Centrifugal force experienced by the element
(mRdθ)ω2RResolving the centrifugal force into rectangular components,
Since the horizontal components cancel each other, the net force on the two symmetric elements is given as
Velocity of the transverse vibration is given as
Linear velocity of the string, V = ωR
∴ Speed of the disturbance, V' = V
Q.26. A heavy but uniform rope of length L is suspended from a ceiling.
(a) Write the velocity of a transverse wave travelling on the string as a function of the distance from the lower end.
(b) If the rope is given a sudden sideways jerk at the bottom, how long will it take for the pulse to reach the ceiling?
(c) A particle is dropped from the ceiling at the instant the bottom end is given the jerk. Where will the particle meet the pulse?
(a) Let m be the mass per unit length of the string.
Consider an element at a distance x from the lower end.
Here,
Weight acting downwards = (mx)g
∴ Tension in the string at the upper part = mgx
The velocity of transverse vibration is given as
(b) Let the time taken be dt for the small displacement dx.
Thus, we have:
(c) Suppose after time t, the pulse meets the particle at a distance y from the lower end of the rope.
Now,
∴ Distance travelled by the particle in this time, S = L - y
Using the equation of motion, we get:
Thus, the particle will meet the pulse at a distance
L/3 from the lower end.
Q.27. Two long strings A and B, each having linear mass density 1.2 x 10-2 kgm-1 , are stretched by different tensions 4⋅8 N and 7⋅5 N respectively and are kept parallel to each other with their left ends at x = 0. Wave pulses are produced on the strings at the left ends at t = 0 on string A and at t = 20 ms on string B. When and where will the pulse on B overtake that on A?
t = 0 in string A
t1 = 0 + 20ms = 20 × 10−3 = 0.02sec
In 0.02secA has travelled 20 × 0.02 = 0.4mt
Relative speed between A and B = 25−20 = 5m/s
Time taken for B for overtake A = s/v = 0.4/5 = 0.08sec
Q.28. A transverse wave of amplitude 0⋅50 mm and frequency 100 Hz is produced on a wire stretched to a tension of 100 N. If the wave speed is 100 m s−1, what average power is the source transmitting to the wire?
Speed of wave = 100m/s = v =
⇒ μ = T/v2 = 0.01kg/m
Power transmitted to the wire = P = 1/2 μω2A2V= 1/2 × 0.01 × (2π×100)2 × 0.00052 ×100W
= 49mW
Q.29. A 200 Hz wave with amplitude 1 mm travels on a long string of linear mass density 6 g m−1 kept under a tension of 60 N.
(a) Find the average power transmitted across a given point on the string.
(b) Find the total energy associated with the wave in a 2⋅0 m long portion of the string.
Given,
Frequency of the wave, f = 200 Hz
Amplitude, A = 1 mm = 10−3 m
Linear mass density, m = 6 gm−3
Applied tension, T = 60 N
Now,
Let the velocity of the wave be v.
Thus, we have:= 102 = 100m/s
(a) Average power is given as
Pavaerage = 2π2mvA2f2
(b) Length of the string = 2 m
Time required to cover this distance:
t = 2/100 = 0.02s
Energy = Power x t
= 0.47 x 0.02
= 9.4 x 10-3 J = 9.4mJ
Q.30. A tuning fork of frequency 440 Hz is attached to a long string of linear mass density 0⋅01 kg m−1 kept under a tension of 49 N. The fork produces transverse waves of amplitude 0⋅50 mm on the string. (a) Find the wave speed and the wavelength of the waves. (b) Find the maximum speed and acceleration of a particle of the string. (c) At what average rate is the tuning fork transmitting energy to the string?
Given,
Frequency of the tuning fork, f = 440 Hz
Linear mass density, m = 0.01 kgm−1
Applied tension, T = 49 N
Amplitude of the transverse wave produce by the fork = 0.50 mm
Let the wavelength of the wave be λ
(a) The speed of the transverse wave is given by
(b) Maximum speed (vmax) and maximum acceleration (amax):
We have:
= 0.67W
Q.31. Two waves, travelling in the same direction through the same region, have equal frequencies, wavelengths and amplitudes. If the amplitude of each wave is 4 mm and the phase difference between the waves is 90°, what is the resultant amplitude?
Given,
Phase difference between the two waves travelling in the same direction,
∅ = 90º = π/2
Frequency f and wavelength
λ are the same. Therefore, ω will be the same.
Let the wave equations of two waves be:
y1 = r sin ωt
y2 = r sin (ωt + π/2)
Here, r is the amplitude.
From the principle of superposition, we get:
∴ Resultant amplitude,
r' = √2r = 4
Q.32. Following figure shows two wave pulses at t = 0 travelling on a string in opposite directions with the same wave speed 50 cm s−1. Sketch the shape of the string at t = 4 ms, 6 ms, 8 ms, and 12 ms.
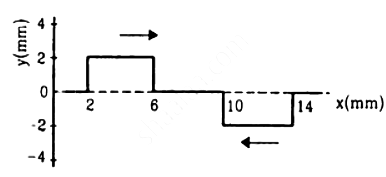
Given,
Speed of the wave pulse travelling in the opposite direction, v = 50 cm s−1 = 500 mm s−1
Distances travelled by the pulses:
Using s = vt, we get:
The shapes of the string at different times are shown in the above.
Q.33. Two waves, each having a frequency of 100 Hz and a wavelength of 2⋅0 cm, are travelling in the same direction on a string. What is the phase difference between the waves (a) if the second wave was produced 0⋅015 s later than the first one at the same place, (b) if the two waves were produced at the same instant but first one was produced a distance 4⋅0 cm behind the second one? (c) If each of the waves has an amplitude of 2⋅0 mm, what would be the amplitudes of the resultant waves in part (a) and (b) ?
Given:
Two waves have same frequency (f), which is 100 Hz.
Wavelength (λ) = 2.0 cm
= 2 x 10-2 cm
Wave speed v = f x λ = 100 x 2 x 10-2m/s
= 2m/s
(a) First wave will travel the distance in 0.015 s.
= x = 0.015 x 2
= 0.03 m
This will be the path difference between the two waves.
So, the corresponding phase difference will be as follows:
(b) Path difference between the two waves, x = 4 cm = 0.04 m
So, the corresponding phase difference will be as follows:
= 4π(c) The waves have same frequency, same wavelength and same amplitude.
Let the wave equation for the two waves be as follows:
y1 = r sin ωt
and y2 = r sin (ωt + ∅)By using the principle of superposition:
Q.34. If the speed of a transverse wave on a stretched string of length 1 m is 60 m−1, what is the fundamental frequency of vibration?
Length of a stretched string (L) = 1 m
Wave speed (v) = 60 m/s
Fundamental frequency (f0) of vibration is given as follows:
Q.35. A wire of length 2⋅00 m is stretched to a tension of 160 N. If the fundamental frequency of vibration is 100 Hz, find its linear mass density.
Given:
l = 2m, f0 = 100Hz, T= 160N
⇒ m = 1g/m.
So, the linear mass density is 1g/m.
Q.36. A steel wire of mass 4⋅0 g and length 80 cm is fixed at the two ends. The tension in the wire is 50 N. Find the frequency and wavelength of the fourth harmonic of the fundamental.
Given:
Mass of the steel wire = 4.0 g
Length of the steel wire = 80 cm = 0.80 m
Tension in the wire = 50 N
Linear mass density (m)
Fundamental frequency ,
First harmonic = 62 . 5 Hz
If f_4 =frequency of the fourth harmonic:
⇒ f4 = 4f0 = 62.5 x 4
⇒ f4 = 250 Hz
Wavelength of thefourth harmonic,
⇒ λ4 = 0.4m = 40 cm
Q.37. A piano wire weighing 6⋅00 g and having a length of 90⋅0 cm emits a fundamental frequency corresponding to the "Middle C" (v = 261.63 Hz). Find the tension in the wire.
Given:
Length of the piano wire (L)= 90.0 cm = 0.90 m
Mass of the wire = 6.00 g = 0.006 kg
Fundamental frequency (fo) = 261.63 Hz
Hence, the tension in the piano wire is 1480 N.
Q.38. A sonometer wire having a length of 1⋅50 m between the bridges vibrates in its second harmonic in resonance with a tuning fork of frequency 256 Hz. What is the speed of the transverse wave on the wire?
Given: Length of the sonometer wire (L) = 1.50 m
Let the first harmonic be f0 and the second harmonic be f1.
According to the question, f1 = 256 Hz
1st harmonic for fundamental frequency,When the fundamental wave is produced, we have:
Q.39. The length of the wire shown in figure between the pulley is 1⋅5 m and its mass is 12⋅0 g. Find the frequency of vibration with which the wire vibrates in two loops leaving the middle point of the wire between the pulleys at rest.
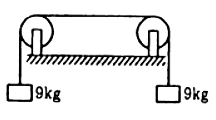
Given:
Length of the wire between two pulleys (L) = 1.5 m
Mass of the wire = 12 gm
Mass per unit length, m, = 12/1.5 g/m
= 8 x 10-3 kg/m
Tension in the wire, T = 9 x g
= 90 N
Fundamental frequency is given by:
For second harmonic (when two loops are produced):
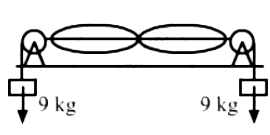
Q.40. A one-metre long stretched string having a mass of 40 g is attached to a tuning fork. The fork vibrates at 128 Hz in a direction perpendicular to the string. What should be the tension in the string if it is to vibrate in four loops?
Given:
Length of the stretched string (L) = 1.00 m
Mass of the string =40 g
String is attached to the tuning fork that vibrates at the frequency (f) = 128 Hz
Linear mass density (m)
= (40 x 10-3) kg/m
No. of loops formed, (n) = 4
Hence, the tension in the string if it is to vibrate in four loops is 164 N.
Q.41. A wire, fixed at both ends is seen to vibrate at a resonant frequency of 240 Hz and also at 320 Hz. (a) What could be the maximum value of the fundamental frequency? (b) If transverse waves can travel on this string at a speed of 40 m s−1, what is its length?
Given:
Wire makes a resonant frequency of 240 Hz and 320 Hz when its both ends are fixed.
Therefore, fundamental frequency (f0) of the wire must be the factor of 240 Hz and 320 Hz.
(a) Maximum value of fundamental frequency, f0 = 80 Hz
(b) Wave speed (v) = 40 m/s
And if λ is the wave length:
Q.42. A string, fixed at both ends, vibrates in a resonant mode with a separation of 2⋅0 cm between the consecutive nodes. For the next higher resonant frequency, this separation is reduced to 1⋅6 cm. Find the length of the string.
Given:
Separation between two consecutive nodes when the string vibrates in resonant mode =2.0 cm
Let there be ' n ' loops and λ be the wavelength.
∴ λ = 2 × Separation between the consecutive nodes
λ2 = 2 × 1.6 = 3.2 cm
Length of the wire is L .
In the first case:
L = (nλ1/2
In the second case:
Q.43. A 660 Hz tuning fork sets up vibration in a string clamped at both ends. The wave speed for a transverse wave on this string is 220 m s−1 and the string vibrates in three loops. (a) Find the length of the string. (b) If the maximum amplitude of a particle is 0⋅5 cm, write a suitable equation describing the motion.
Given:
Frequency (f) = 660 Hz
Wave speed (v) = 220 m/s
(b) Equation of resultant stationary wave can be given by:
Q.44. A particular guitar wire is 30⋅0 cm long and vibrates at a frequency of 196 Hz when no finger is placed on it. The next higher notes on the scale are 220 Hz, 247 Hz, 262 Hz and 294 Hz. How far from the end of the string must the finger be placed to play these notes?
Given:
Length of the guitar wire (L1) = 30.0 cm = 0.30 m
Frequency, when no finger is placed on it, (f1) =196 Hz
And (f2) =220 Hz, (f3) = 247 Hz, (f4) = 262 Hz and (f5) = 294 Hz
The velocity is constant for a medium.
We have:
⇒ L4 = 22.4 cm
And, L5 = 20cm
Q.45. A steel wire fixed at both ends has a fundamental frequency of 200 Hz. A person can hear sound of maximum frequency 14 kHz. What is the highest harmonic that can be played on this string which is audible to the person?
Given:
Fundamental frequency (f0) of the steel wire = 200 Hz
Let the highest harmonic audible to the person be n.
Frequency of the highest harmonic, f' = 14000 Hz
∴ f' = nf0 ...(1)
Thus, the highest harmonic audible to man is the 70th harmonic.
Q.46. Three resonant frequencies of a string are 90, 150 and 210 Hz. (a) Find the highest possible fundamental frequency of vibration of this string. (b) Which harmonics of the fundamental are the given frequencies? (c) Which overtones are these frequencies? (d) If the length of the string is 80 cm, what would be the speed of a transverse wave on this string?
Given:
Let the three resonant frequencies of a string be
f1 = 90Hz
f2 = 150Hz
f3 = 210Hz
(a) So, the highest possible fundamental frequency of the string is f = 30 Hz because f1, f2 and f3 are the integral multiples of 30 Hz.
(b) So, these frequencies can be written as follows:
f1 = 3f
f2 = 5f
f3 = 7fHence, f1, f2, and f3 are the third harmonic, the fifth harmonic and the seventh harmonic, respectively.
(c) The frequencies in the string are f, 2f, 3f, 4f, 5f ...
∴ 3f = 2nd overtone and 3rd harmonic
5f = 4th overtone and 5th harmonic
7th= 6th overtone and 7th harmonic
(d) Length of the string (L) = 80 cm = 0.8 m
Let the speed of the wave be v.
So, the frequency of the third harmonic is given by:
= 30 x 2 x 80
= 4800 c/m
⇒ v = 48 m/s
Q.47. Two wires are kept tight between the same pair of supports. The tensions in the wires are in the ratio 2 : 1 the radii are in the ratio 3 : 1 and the densities are in the ratio 1 : 2. Find the ratio of their fundamental frequencies.
Given:
The tensions in the two wires are in the ratio of 2:1.
Let the length of the wire be L.
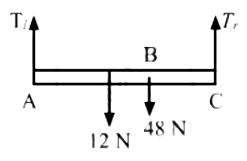
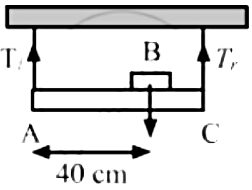
Q.48. A uniform horizontal rod of length 40 cm and mass 1⋅2 kg is supported by two identical wires as shown in figure. Where should a mass of 4⋅8 kg be placed on the rod so that the same tuning fork may excite the wire on left into its fundamental vibrations and that on right into its first overtone? Take g = 10 m s−2.
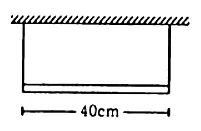
Given:
Length of the rod (L) = 40 cm = 0.40 m
Mass of the rod (m) = 1.2 kg
Let the mass of 4.8 kg be placed at x distance from the left.
As per the question, frequency on the left side = f0
Frequency on the right side = 2f0
Let tension be T1 and T2 on the left and the right side, respectively.
From the free body diagram:
T1 + T2 = 48 + 12 = 60 N
⇒ 4T2 + T2 = 5T2 = 60 N [ Using equation (1)]
∴ T2 = 12N
And T1 = 48N
Now, taking moment about point A:
Therefore, the mass should be placed at a distance of 5 cm from the left end.
Q.49. Figure shows an aluminium wire of length 60 cm joined to a steel wire of length 80 cm and stretched between two fixed supports. The tension produced is 40 N. The cross-sectional area of the steel wire is 1⋅0 mm2 and that of the aluminium wire is 3⋅0 mm2. What could be the minimum frequency of a tuning fork which can produce standing waves in the system with the joint as a node? The density of aluminium is 2⋅6 g cm−3 and that of steel is 7⋅8 g cm−3.
PS = 7.8 g m/cm3
PA = 2.6 g m/cm3
ms = PSAS
= 7.8 × 10−2 gm/cm
(m = mass per unit length)
= 7.8 × 10−3 kg/m
mA = PAAA
= 2.6 × 10−2 × 3 gm/cm
7.8 × 10−2 g m/cm
7.8 × 10−3 kg/m
A node is always placed in the joint. Since aluminium and steel rod has same mass per unit length, velocity of wave in both of them is same.
= 71.6 m/s
For minimum frequency there would be maximum wavelength.
For maximum wavelength minimum no. of loops are to be produced.
∴ Maximum distance of a loop = 20 cm
⇒ Wavelength = λ = 2 × 20
= 40 c m = 0.4 m
Q.50. A string of length L fixed at both ends vibrates in its fundamental mode at a frequency ν and a maximum amplitude A. (a) Find the wavelength and the wave number k. (b). Take the origin at one end of the string and the X-axis along the string. Take the Y-axis along the direction of the displacement. Take t = 0 at the instant when the middle point of the string passes through its mean position and is going towards the positive y-direction. Write the equation describing the standing wave.
Given:
Length of the string = L
Velocity of wave is given as:
Q.51. A 2 m long string fixed at both ends is set into vibrations in its first overtone. The wave speed on the string is 200 ms−1 and the amplitude is 0⋅5 cm. (a) Find the wavelength and the frequency. (b) Write the equation giving the displacement of different points as a function of time. Choose the X-axis along the string with the origin at one end and t = 0 at the instant when the point x = 50 cm has reached its maximum displacement.
Given:
Length of the string (L) = 2.0 m
Wave speed on the string in its first overtone (v) = 200 m/s
Amplitude (A) = 0.5 cm
(a) Wavelength and frequency of the string when it is vibrating in its 1st overtone (n = 2):
(b) The stationary wave equation is given by:
Q.52. The equation for the vibration of a string, fixed at both ends vibrating in its third harmonic, is given by
y = (0.4cm) sin [0.314cm-1)x] cos [600πs-1)t]
(a) What is the frequency of vibration?
(b) What are the positions of the nodes?
(c) What is the length of the string?
(d) What is the wavelength and the speed of two travelling waves that can interfere to give this vibration?
Given:
The stationary wave equation of a string vibrating in its third harmonic is given by
y = (0.4 cm) sin [(0.314 cm−1) x]cos [(.600 πs−1) t]
By comparing with standard equation,
y = A sin (kx) cos (ωt)
(a) From the above equation, we can infer the following:
(b) Therefore, the nodes are located at 0cm, 10 cm, 20 cm, 30 cm.
λ and v are the wavelength and velocity of the waves that interfere to give this vibration.
λ = 20cm
⇒ v = 60 m/s
Q.53. The equation of a standing wave, produced on a string fixed at both ends, is
y = (0.4 cm) sin [(0.314 cm−1) x]cos [(.600 πs−1) t]
What could be the smallest length of the string?
Given:
Equation of the standing wave:y = (0.4 cm) sin [(0.314 cm−1) x]cos [(.600 πs−1) t]
For the smallest length, putting n = 1:
Therefore, the required length of the string is 10 cm.
Q.54. A 40 cm wire having a mass of 3⋅2 g is stretched between two fixed supports 40⋅05 cm apart. In its fundamental mode, the wire vibrates at 220 Hz. If the area of cross section of the wire is 1⋅0 mm2, find its Young modulus.
Given:
Length of the wire (L) = 40 cm = 0.40 m
Mass of the wire = 3.2 g = 0.003 kg
Distance between the two fixed supports of the wire = 40.05 cm
Fundamental mode frequency = 220 Hz
Therefore, linear mass density of the wire (m) is given by:
Hence, the required Young's modulus of the wire is
1.985 x 1011 N/m2
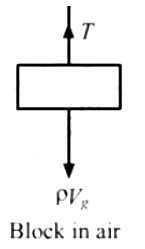
Q.55. The Following figure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning for. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. Find the density of the material of the block.
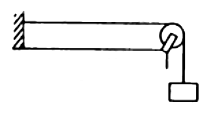
Density of the block = ρ
Volume of block = V
∴ Weight of the block is, W = ρVg
∴ Tension in the string, T = W
The tuning fork resonates with different frequencies in the two cases.
Let the tenth harmonic be f10.
The frequency (f) of the tuning fork is same.
Therefore, the required density is 5.8 x 103 kg/m3
Q.56. A 2⋅00 m-long rope, having a mass of 80 g, is fixed at one end and is tied to a light string at the other end. The tension in the string is 256 N. (a) Find the frequencies of the fundamental and the first two overtones. (b) Find the wavelength in the fundamental and the first two overtones.
Given:
Length of the long rope (L) = 2.00 m
Mass of the rope = 80 g = 0.08 kg
Tension (T) = 256 N
Linear mass density, m
⇒ v = 80 m/s
For fundamental frequency:(a) The frequency overtones are given below:
1st overtone = 3f = 30 Hz
2nd overtone = 5f = 50 Hz
Hence, the wavelengths are 8 m, 2.67 m and 1.6 m, respectively.
Q.57. A heavy string is tied at one end to a movable support and to a light thread at the other end as shown in following figure. The thread goes over a fixed pulley and supports a weight to produce a tension. The lowest frequency with which the heavy string resonates is 120 Hz. If the movable support is pushed to the right by 10 cm so that the joint is placed on the pulley, what will be the minimum frequency at which the heavy string can resonate?
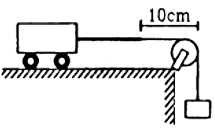
Let T be the tension in the string and m be the mass per unit length of the heavy string.
In the first part of the question, the heavy string is fixed at only one end.
So, the lowest frequency is given by:When the movable support is pushed by 10 cm to the right, the joint is placed on the pulley and the heavy string becomes fixed at both the ends (keeping T and m same).
Now, the lowest frequency is given by:Dividing equation (2) by equation (1), we get:
f'0 = 2f0 = 240 Hz
|
134 docs
|
FAQs on HC Verma Questions and Solutions: Chapter 15: Wave Motion & Waves on a String - 2 - HC Verma Solutions - JEE
| 1. How do waves on a string propagate? |  |
| 2. What factors determine the speed of waves on a string? |  |
| 3. How are the amplitude and frequency of waves on a string related? |  |
| 4. What happens to the wavelength of waves on a string if the tension is increased? |  |
| 5. Can waves on a string be reflected? |  |