Non-Uniform Acceleration: Motion in One Dimension | Physics for JEE Main & Advanced PDF Download
| Table of contents |

|
| Introduction |

|
| Non-Uniform Acceleration |

|
| Important Formulas and Derivation |

|
| Relevant Graphs of Non Uniformly Accelerated Motion |

|
| Solved Examples on Non Uniformly Accelerated Motion |

|
Introduction
In the course of a train journey, it is common to observe a sudden jerk as the train departs from the platform. As the train gradually gains speed, a continuous force can be felt pushing against your back. Conversely, when the train slows down in response to a signal, you experience a forward-pushing force. This recurring pattern of motion throughout the train's journey exemplifies non-uniformly accelerated motion. Similar sensations can also be experienced when traveling in heavy traffic while driving a car or riding a bike. In this discussion, we will delve into the topic in greater detail.
Non-Uniform Acceleration
Non-Uniform Acceleration refers to a situation where the acceleration of an object during motion is not constant. Acceleration is the measure of velocity's rate of change, represented as dv/dt. In the case of non-uniform acceleration, the "a-t" graph will exhibit a non-linear pattern that varies over time. An illustrative example is the motion of a train. Initially, the train experiences a high acceleration to overcome static inertia and continues to accelerate until it needs to decelerate upon receiving a signal. This results in significant changes in acceleration throughout the entire journey, indicating non-uniform acceleration.
Important Formulas and Derivation
In this section, we provide some non-uniform acceleration formulas that may be useful for solving related problems. If v is the velocity of a particle, and “a” be its acceleration (rate of change of velocity), then,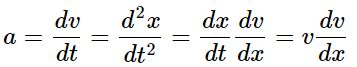
As velocity (rate of change of displacement),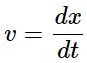
This is the basic step of formulas to be used.
1. If the given acceleration is a function of time, then,
Given, 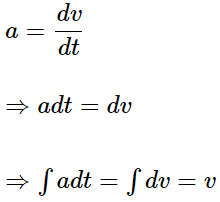
Now, 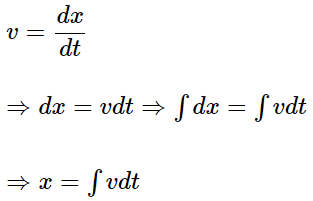
2. If the acceleration is a function of velocity,
Given, 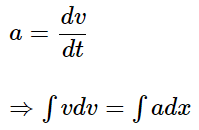
We can use these two cases to solve the non-uniform accelerated motion of a particle.
 |
Download the notes
Non-Uniform Acceleration: Motion in One Dimension
|
Download as PDF |
Relevant Graphs of Non Uniformly Accelerated Motion
Here, we are going to discuss a few important graphs for this concept.
1. Velocity Time Graph for Non Uniformly Accelerated Motion
Note that in the v-t graph, the slope at any point ‘t’ is the acceleration at that point. As the slope of the graph is not constant, it cannot be linear.
Here are some possible v-t graphs.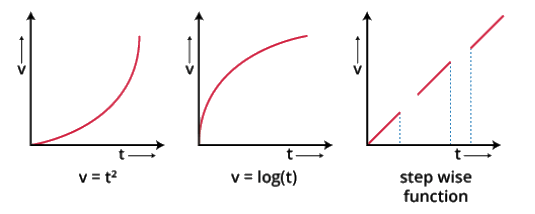 Velocity-Time Graph for some Non-Uniform Acceleration
Velocity-Time Graph for some Non-Uniform Acceleration
For the three cases, observe that all the graphs are not linear. Hence, their slope would not be constant, which is non-uniform acceleration. We can physically calculate the acceleration and check its non-uniform accelerated motion.
2. Non Uniformly Accelerated Motion Graph (a-t)
As we know, acceleration is not constant. The graphs will not be lines parallel to the x-axis for the entire time. Now, we will take a few examples of the graphs.
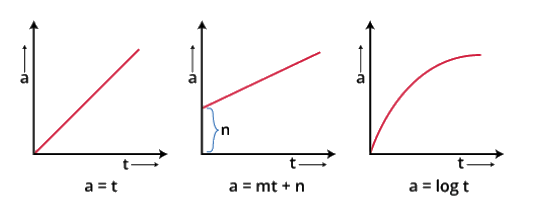 Acceleration-Time Graph for Non-Uniform Accelerated Motion
Acceleration-Time Graph for Non-Uniform Accelerated Motion
For these cases, da/dt ≠ 0. It is another way to check the non-uniformity in the acceleration of these motions. Now, here is an interesting example of a graph.
Note: Area under a-t graph represents velocity, while the area under v-t graph represents displacement.
Solved Examples on Non Uniformly Accelerated Motion
Consider you are moving in a motorcycle in a heavy traffic jam. The figure below shows the “a-t” graph of your motion. Find out the highest velocity in the motion.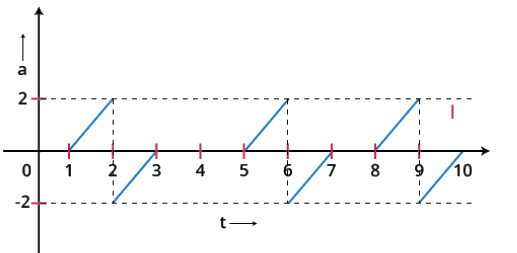
Solution: In order to find the maximum velocity, we first need to find the relationship between the acceleration and the time. This can be found by writing the equation of the line between the y and x axis for the above graph.
We know that the equation of a line is given as
y = mx + c
Here, m is the slope and c is the y intercept. For our case, y will be a and x will be t.
Now let’s consider the positive interval from t=1 to 2 sec.
In this interval, the slope is 2.
Also, since the line is starting from t = 1, the equation will be a=2(t-1).
We will be assuming that the initial velocity is 0 since it is not given.
Integrating both sides of the equation gives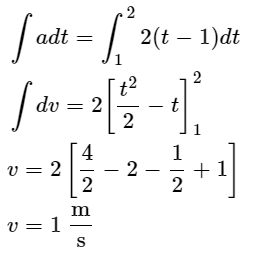
Since the other interval from t = 2 to t = 3 has a negative acceleration, the velocity will increase from t=1 to t = 2 and will have a maximum value at t = 2 which will be 1 m/s.
So, the maximum velocity is 1 m/s.
|
291 videos|648 docs|183 tests
|




























