Law of Conservation of Energy - JEE PDF Download

Introduction

The Law of Conservation of Energy asserts that energy cannot be created or destroyed but can only change from one form to another. When considering all forms of energy within an isolated system, the total energy remains constant. This principle applies to all forms of energy and can be summarized as follows: Within a closed system, where the system is isolated from its surroundings, the total energy of the system remains conserved.

Example of Energy Transformation

So in an isolated system such as the universe, if there is a loss of energy in some part of it, there must be a gain of an equal amount of energy in some other part of the universe. Although this principle cannot be proved, there is no known example of a violation of the principle of conservation of energy.
The amount of energy in any system is determined by the following equation:
U_T = U_i + W + Q

• U_T is the total energy of a system
• U_i is the initial energy of a system
• Q is the heat added or removed from the system
• W is the work done by or on the system

The change in the internal energy of the system is determined using the equation

ΔU = W + Q

Law of Conservation of Energy Derivation

Let's consider a point A on the tree, which is at a height 'H' from the ground. At this point, the fruit is at rest, having zero velocity, and therefore, its potential energy is maximum.
The expression for the energy at point A can be written as:

E = mgH ———- (1)
As the fruit falls, its potential energy decreases, while its kinetic energy increases. Let's consider a point B near the bottom of the tree, where the fruit is freely falling under gravity. At this point, the fruit is at a height 'X' from the ground and has a certain speed. Thus, it possesses both kinetic and potential energy.
The total energy at point B can be expressed as the sum of kinetic energy (K.E) and potential energy (P.E):
E = K.E + P.E
The potential energy at point B can be given by:
P.E = mgX ——— (2)
Based on the third equation of motion,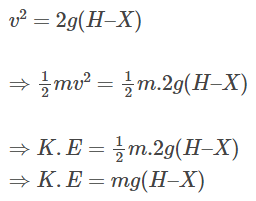

K.E=mg(H-X)——– (3)
Using (1), (2) and (3)
E = mg(H – X) + mgX
E = mg(H – X + X)
E = mgH
Similarly, if we see the energy at point C, which is at the bottom of the tree, it will come out to be mgH. We can see as the fruit is falling to the bottom, here, potential energy is getting converted into kinetic energy. So there must be a point where kinetic energy becomes equal to potential energy. Suppose we need to find that height ‘x’ from the ground. We know at that point,
K.E = P.E
P.E = K.E = F/2——– (4)
As the body is at height X from the ground,
P.E = mgX ——— (5)
Using (4) and (5) we get,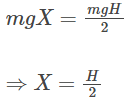

H/2 is referred to as the new height.

Energy Conservation

Energy conservation is not about limiting the use of resources which will finally run out altogether. The ideal way of conservation would be reducing demand on a limited supply and enabling that supply to begin to rebuild itself. Many times the best way of doing this is to replace the energy used with an alternative.

Law of Conservation of Energy Examples

The Law of Conservation of Energy plays a fundamental role in various physical phenomena. Many inventions and devices operate based on the principle that energy is conserved during its transformation from one form to another. Let's explore a few examples:

• Torch: In a torch, the chemical energy stored in the batteries is converted into electrical energy, which is then transformed into light and heat energy.
• Hydroelectric Power Plants: Water falling from a height onto the turbines in hydroelectric power plants converts potential energy into kinetic energy, which subsequently rotates the turbines and generates electricity. Here, the potential energy of the water is converted into the kinetic energy of the turbine, which is further transformed into electrical energy.
• Loudspeaker: Electrical energy is converted into sound energy in a loudspeaker, allowing it to produce audible sound waves.
• Microphone: A microphone works by converting sound energy into electrical energy, allowing it to capture and transmit sound signals.
• Generator: A generator converts mechanical energy into electrical energy. Mechanical energy, often obtained from a rotating turbine or engine, drives the generator to produce electricity.
• Combustion: When fuels are burnt, chemical energy stored in the fuel is converted into heat and light energy. This principle is utilized in various applications, including heating systems and combustion engines.
• Human Body: In the human body, the chemical energy derived from food is converted into thermal energy through metabolic processes. This conversion provides the necessary heat to maintain body temperature.

These examples highlight the diverse applications of the Law of Conservation of Energy, demonstrating how energy is transformed but remains conserved throughout various processes and devices.