Equipotential Surface - Properties and Examples - JEE PDF Download

Introduction

An equipotential surface is defined as a surface comprised of points that possess an equal potential. When traversing an equipotential surface, no work is required to move a charge from one point to another. In simpler terms, any surface with a consistent electric potential at every point can be classified as an equipotential surface.

Equipotential Points and Lines

Within an electric field, if the points are all at the same electric potential, they are referred to as equipotential points. Connecting these points with a line or curve creates an equipotential line. Furthermore, if these points lie on a surface, we designate it as an equipotential surface. Finally, if these equipotential points are dispersed throughout a space or volume, we classify it as an equipotential volume.

Work Done on an Equipotential Surface

When it comes to moving a charge between two points on an equipotential surface, the work done is always zero. The formula for calculating the work done is given by W = q₀(VA – VB). However, since VA – VB is always equal to zero for an equipotential surface, the total work done is naturally W = 0.

Properties of Equipotential Surfaces

To gain a comprehensive understanding of equipotential surfaces, let's explore their key properties:

• Perpendicular Electric Field: The electric field is always perpendicular to an equipotential surface.
• Non-intersecting Surfaces: Two equipotential surfaces can never intersect.
• Point Charge: For a point charge, the equipotential surfaces manifest as concentric spherical shells.
• Uniform Electric Field: In a uniform electric field, the equipotential surfaces take the form of planes perpendicular to the x-axis.
• Directional Flow: The direction of the equipotential surface extends from high potential to low potential.
• Hollow-Charged Spherical Conductor: Inside a hollow-charged spherical conductor, the potential remains constant, turning it into an equipotential volume.
• Effortless Charge Movement: No work is required to move a charge from the center to the surface of a hollow-charged spherical conductor.
• Isolated Point Charge: For an isolated point charge, the equipotential surface takes the shape of a sphere, with concentric spheres representing different equipotential surfaces.
• Uniform Electric Field (Continued): In a uniform electric field, any plane perpendicular to the field's direction serves as an equipotential surface.
• Field Strength Identification: The spacing between equipotential surfaces aids in identifying regions of strong and weak electric fields. This can be determined through the formula E = -dV/dr, suggesting that E is inversely proportional to the spacing 1/dr.

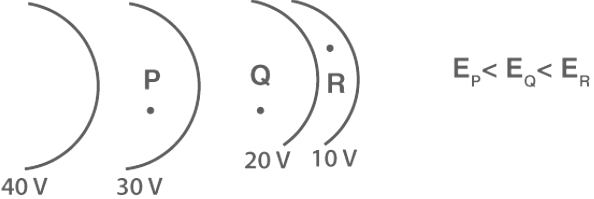
Problems on Equipotential Surface

Q.1: A charged particle (q =1.4 mC) moves a distance of 0.4 m along an equipotential surface of 10 V. Calculate the work done by the field during this motion.
Solution: The work done by the field is given by the expression
W = -qΔV
Since ΔV = 0, for equipotential surfaces, the work done is zero, W = 0.

Q.2: A positive particle of charge 1.0 C accelerates in a uniform electric field of 100 V/m. The particle started from rest on an equipotential plane of 50 V. After t = 0.0002 seconds, the particle is on an equipotential plane of V = 10 volts. Determine the distance travelled by the particle.
Solution: The work done in moving a charge in an equipotential surface is given by
W = -qΔV
Substituting the values, we get
W = (-1.0, C) (10V – 50V) = 40 J
We know that the work done in moving a charge in an electric field:
W = qEd
40 = (1.0) (100)d
d = 0.4m

Q.3: An electron of mass (m) and charge (e) is released from rest in a uniform electric field of 106 newton/coulomb. Compute its acceleration. Also, find the time taken by the electron to attain a speed of 0.1 c, where c is the velocity of light. (m = 9.1 × 10^–31 kg, e = 1.6 × 10^–19 coulomb and c = 3 ×10⁸ metre/sec).
Solution: The force experienced by the electron is
F = Ee = 10⁶ (1.6 × 10^–19)
= 1.6 × 10^–13 newton
The acceleration of the electron is given by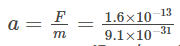

= 1.8 × 1017 m/sec²
The initial velocity = zero.
Let t be the time taken by the electron to attain a final speed of 0.1 c.
Now v = u + at or v = at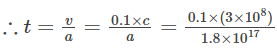

= 1.7 × 10¹⁰ sec.