Solved Examples: Domain & Range - JEE PDF Download

Q1.
(a) State the domain and range of f (x)=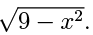
Solution: The domain of f (x)=   is all real x where −3 ≤ x ≤ 3. The range is all real y such that 0 ≤ y ≤ 3.
(b) Sketch the graph of y =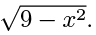
Solution: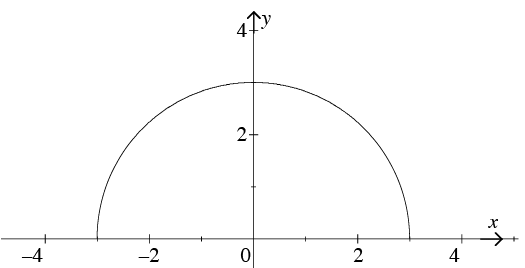
The graph of f (x) =  

Q2. Sketch the following functions stating the domain and range of each:
(a) y =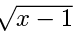
Solution:

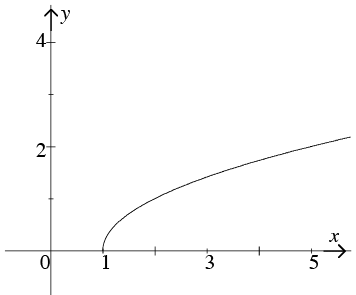
The graph of y = 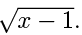The domain is all real x ≥ 1 and the range is all real y ≥ 0.
(b) y = |2x|
Solution:
The graph of y = |2x|. Its domain is all real x and range all real y ≥ 0
(c) y = 1/x−4
Solution:

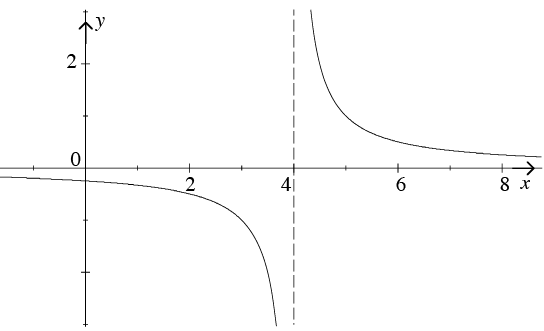
The graph of y = 1/x−4 . The domain is all real x = 4 and the range is all real y = 0.
(d) y = |2x|− 1.
Solution:

The graph of y = |2x|− 1. The domain is all real x, and the range is all real y ≥−1.

Q3. Explain the meanings of function, domain and range. Discuss whether or not y2 = x3 is a function.

Solution: y² = x³ is not a function. If x = 1, then y² = 1 and y = 1 or y = −1.

Q4. Sketch the following relations, showing all intercepts and features. State which ones are functions giving their domain and range.
(a) y =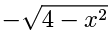  
Solution:

The graph of y = . This is a function with the domain: all real x such that −2 ≤ x ≤ 2 and range: all real y such that −2 ≤ y ≤ 0.

(b) |x|−|y| =0
Solution:

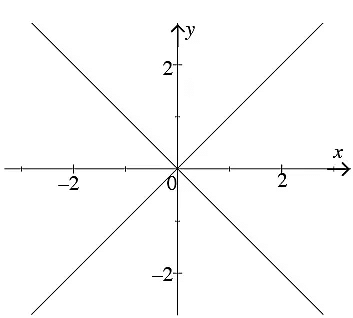
The graph of |x|−|y| = 0. This is not the graph of a function.

(c) y = x³
Solution:

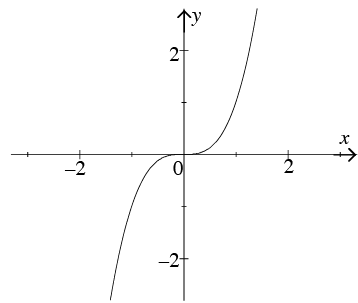
The graph of y = x³. This is a function with the domain: all real x and range: all real y.

(d) y = x/|x| ,x = 0
Solution: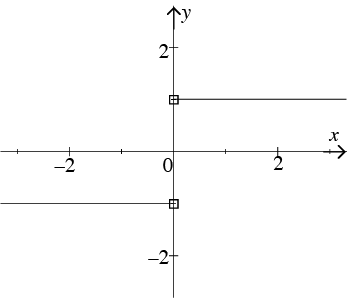

The graph of y = x/|x| . This is the graph of a function that is not defined at x = 0. Its domain is all real x = 0, and the range is y = ±1.
(e) |y| = x.
Solution: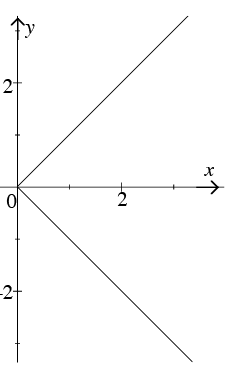
The graph of |y| = x. This is not the graph of a function.

Q.5. Write down the values of x which are not in the domain of the following functions:
(a) f (x) =
Solution: The values of x in the interval 0 <x< 4 are not in the domain of the function.
(b) g(x) =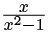
Solution: x = 1 and x = −1 are not in the domain of the function.