Area of Triangle in Determinant Form - JEE PDF Download

How is the Area of a Triangle Calculated Using Determinants?

When the vertices of a triangle are provided, the area of the triangle can be computed using the determinant form. Suppose we have a triangle ABC with vertices A(x₁, y₁), B(x_2, y₂), and C(x₃, y₃). In this case, the area can be determined by the expression (1/2) [x₁ (y₂ - y₃) + x2 (y₃ - y₁) + x₃ (y₁ - y₂)]. While the general formula for the area of a triangle involves half the product of its base and height, in coordinate geometry, if the coordinates of the triangle's vertices are known, we can utilize the determinant form to calculate the area. 

Determinant Form Formula for the Area of a Triangle

When calculating the area of a triangle using the determinant form formula, the result obtained is a scalar value that can be either positive or negative. However, since the area of a triangle cannot be negative, we take the absolute value of the determinant to represent the triangle's area. In the context of a Cartesian plane, if the vertices of a triangle ABC are defined as A(x1, y1), B(x2, y2), and C(x3, y3), the formula for the area of the triangle in determinant form is expressed as follows: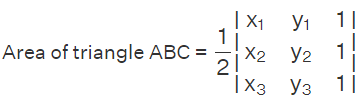

After simplification, this formula of area of triangle in determinant form can also be written as:
Area of triangle ABC = (1/2) | [x₁ (y₂ - y₃) + x₂ (y₃ - y₁) + x₃ (y₁ - y₂)] |

How to Determine Area of Triangle in Determinant Form?

Now that we are familiar with the formula for calculating the area of a triangle using the determinant form, let's explore some examples to better grasp its application. We will consider a triangle ABC, and the coordinates of its vertices will be provided.
Example 1: Calculate the area of a triangle using the determinant form when the vertices are A(0, 0), B(0, -5), and C(8, 0).
Solution: To determine the area of triangle ABC, we will apply the formula for the area in determinant form, which is obtained by substituting the coordinates of the vertices into the formula.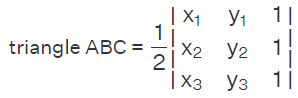

Here x₁ = 0, x₂ = 0, x₃ = 8, y₁ = 0, y₂ = -5, y₃ = 0. Therefore, the area is given by,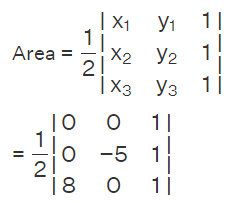

= (1/2) | [0 (-5 - 0) + 0 (0 - 0) + 8 (0 - (-5))] |
= (1/2) | 0 + 0 + 8 × 5 |
= (1/2) × 40
= 20 square units
Example 2: Compute the area of a triangle PQR by the determinant method whose vertices are P(-3, -5), Q(-8, 5), and R(1, 2).
Solution: To find the area of triangle PQR, we will use the formula, Area of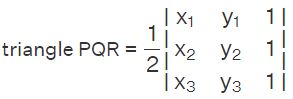

Here x₁ = -3, x₂ = -8, x₃ = 1, y₁ = -5, y₂ = 5, y₃ = 2. Therefore, the area is given by,
Area = (1/2) | [x₁ (y₂ - y₃) + x₂ (y₃ - y₁) + x₃ (y₁ - y₂)] |
= (1/2) | [-3 (5 - 2) + (-8) (2 - (-5)) + 1 (-5 - 5)] |
= (1/2) | [-3 (3) - 8 (7) + 1 (-10)] |
= (1/2) |- 9 - 56 - 10|
= (1/2) |-75|
= (1/2) × 75
= 37.5 square units