Cramer's Rule - Definition, Formula and Conditions | Mathematics for NDA PDF Download
| Table of contents |

|
| Introduction |

|
| Cramer’s Rule Formula |

|
| Cramer’s Rule Example – 2×2 |

|
| Cramer’s Rule 3×3 |

|
| Cramer’s Rule Example – 3×3 |

|
| Cramer’s Rule Conditions |

|
| Cramer’s Rule Questions |

|
Introduction
In the field of linear algebra, Cramer's rule provides a specific formula that is employed to solve systems of linear equations, where the number of equations matches the number of unknown variables. This rule is particularly effective when the system has a unique solution. The rule is named after Gabriel Cramer (1704-1752), who presented the formula for an arbitrary number of unknowns in 1750. It is widely used as a method to obtain solutions for systems of equations formed using matrices. The solution obtained using Cramer's rule is expressed in terms of determinants, specifically the determinant of the coefficient matrix and matrices derived from it by substituting one column with the column vector composed of the right-hand sides of the equations.
Definition of Cramer's Rule
Cramer's rule is a significant method employed for solving systems of equations. In this approach, the values of the variables within the system are computed by utilizing determinants of matrices. As a result, Cramer's rule is also referred to as the determinant method.
Cramer’s Rule Formula
Consider a system of linear equations with n variables x₁, x₂, x₃, …, xₙ written in the matrix form AX = B.
Here,
A = Coefficient matrix (must be a square matrix)
X = Column matrix with variables
B = Column matrix with the constants (which are on the right side of the equations)
Now, we have to find the determinants as:
D = |A|, Dx1, Dx2, Dx3,…, Dxn
Here, Dxi for i = 1, 2, 3,…, n is the same determinant as D such that the column is replaced with B.
Thus,
x1 = Dx1/D; x2 = Dx2/D; x3 = Dx3/D; ….; xn = Dxn/D {where D is not equal to 0}
Let’s have a look at the formulas of Cramer’s rule for 2×2 and 3×3 matrices.
Cramer’s Rule 2×2
Cramer’s rule for the 2×2 matrix is applied to solve the system of equations in two variables.
Let us consider two linear equations in two variables.
a1x + b1y = c1
a2x + b2y = c2
Let us write these two equations in the form of AX = B.
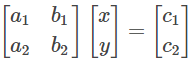
Here,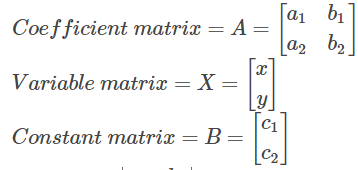
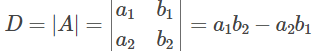
And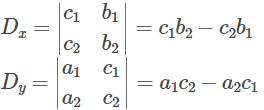
Therefore,
x = Dx/D
y = Dy/D
Cramer’s Rule Example – 2×2
Ex. Solve the following system of equations using Cramer’s rule:
2x – y = 5
x + y = 4
Solution:
Given,
2x – y = 5
x + y = 4
Let us write these equations in the form AX = B.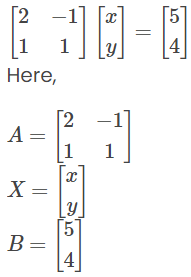
Now,
D = |A|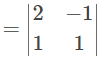
= 2(1) – (-1)1
= 2 + 1
= 3 ≠ 0
So, the given system of equations has a unique solution.
= 5(1) – (-1)(4)
= 5 + 4
= 9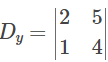
= 2(4) – 5(1)
= 8 – 5
= 3
Therefore,
x = Dx/D = 9/3 = 3
y = Dy/D = 3/3 = 1
Cramer’s Rule 3×3
To find the Cramer’s rule formula for a 3×3 matrix, we need to consider the system of 3 equations with three variables.
Consider:
a1x + b1y + c1z = d1
a2x + b2y + c2z = d2
a3x + b3y + c3z = d3
Let us write these equations in the form AX = B.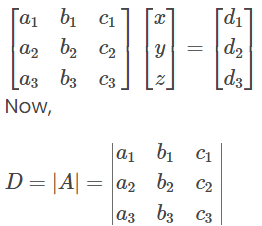
And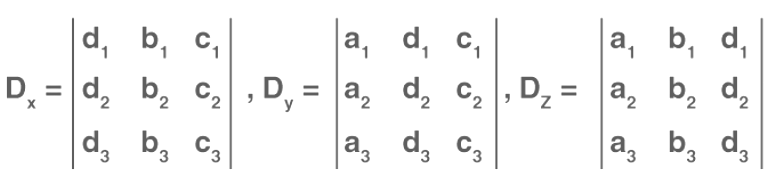
Therefore, x = Dx/D, y = Dy/D, z = Dz/D; D ≠ 0
Go through the example given below to learn how to solve Cramer’s rule for the 3×3 matrix.
Cramer’s Rule Example – 3×3
Ex. Solve the following system of equations using Cramer’s rule:
x + y + z =6
y + 3z = 11
x + z =2y or x – 2y + z = 0
Solution: Given,
x + y + z =6
y + 3z = 11
x + z =2y or x – 2y + z = 0
Let us write these equations in the form AX = B.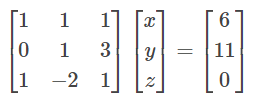
Now,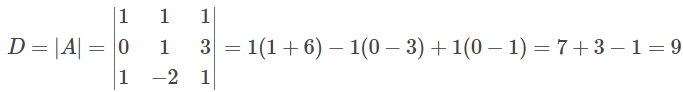
D ≠ 0 so the given system of equations has a unique solution.
Also,
Thus, x = Dx/D = 9/9 = 1
y = Dy/D = 18/9 = 2
z = Dz/D = 27/9 = 3
Cramer’s Rule Conditions
There are certain conditions to applying Cramer’s rule for solving the given system of equations. Some of them include the following:
- Cramer’s rule fails for the system of equations in which D = 0 since for finding the values of unknowns, D must be in the denominator and hence these values go undefined.
Also, when D = 0, there will be two possibilities for which:The system may have no solution.
The system may have an infinite number of solutions.
From this, we can say that at least one of the numerator determinants is a 0 (that means infinitely many solutions) or none of the numerator determinants is 0 (that means no solution)
- If D ≠ 0, we say that the system AX = B has a unique solution.
Thus, Cramer’s rule helps us determine whether the given system has “no solution” or “infinite number of solutions”, using the determinants we calculate to apply the rule.
Cramer’s Rule Questions
- Solve the following system of equations by Cramer’s rule: 2x – 3y + 5z = 113x + 2y – 4z = – 5
x + y – 2z = – 3 - Solve the following system of linear equations using Cramer’s rule:5x + 7y = -24x + 6y = -3
- The cost of 4 kg onion, 3 kg wheat and 2 kg rice is Rs 60. The cost of 2 kg onion, 4 kg wheat and 6 kg rice is Rs 90. The cost of 6 kg onion 2 kg wheat, and 3 kg rice is Rs 70. Find the cost of each item per kg by Cramer’s rule.
|
290 videos|298 docs|232 tests
|















