Equation of a Plane: Vector, Scalar, and General Forms - JEE PDF Download

Equation of Plane

Equation of plane represents a plane surface, in a three-dimensional space. Equation of a plane can be derived through four different methods, based on the input values given. The equation of the plane can be expressed either in cartesian form or vector form.
Let us check the different methods of forming an equation of plane, the derivation of different methods, and the different forms of the equation of plane.

What are the Equations of Plane?

The equation of a plane can be computed through different methods based on the available inputs values about the plane. The following are the four different expressions for the equation of plane.

• Equation of a plane at a perpendicular distance d from the origin and having a unit normal vector 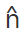  is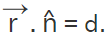 
• The equation of a plane perpendicular to a given vector 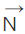 and passing through a point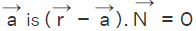   
• The equation of a plane passing through three non collinear points  
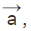
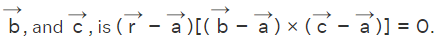
• The equation of a plane passing through the intersection of two planes

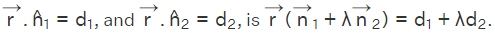
Derivation of Equations of Plane

Here we shall aim at understanding the proof of different methods to find the equation of plane.

Equation of a Plane in Normal Form

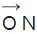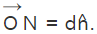Let us consider a normal   to the plane. Normal is a perpendicular line drawn from the origin O to a point N in the plane, such that  is perpendicular to the pane. Let the length of the normal   be d units, such that   Further, we shall consider a point P in the plane, having a position vector of  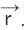We now have  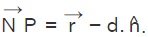 Also 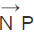 and 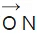   are perpendicular to each other, and the dot product of these two perpendicular lines is equal to 0. Finally, we have the following expression for the dot product of these two lines as follows.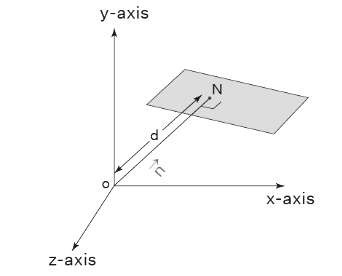

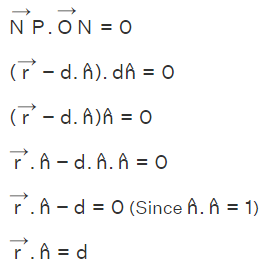
Equation of a Plane Perpendicular to a given vector and through a Point

Let us consider a point A in the plane with a position vector 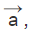 and a vector which is perpendicular to this plane. Let us consider another point P in the plane having a position vector 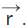 The line  
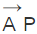�→� lies in this referred plane and is perpendicular to the normal  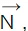 Here we have the dot product of these two lines equal to zero.   Solving this further we have the following expression.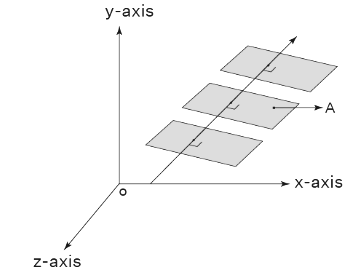 

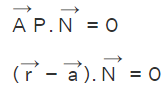
Equation of a Plane Passing Through Three Non Collinear Points

Let us consider three noncollinear points A, B, C in the required plane and having the position vectors as 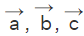 respectively. The product  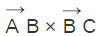gives a vector which is perpendicular to this plane, and it can be referred as the normal to the plane. Here we consider a point P in the plane with the position vector  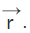The equation of a plane passing through this point P and perpendicular to  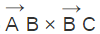can be obtained from the dot product of the line  and the perpendicular 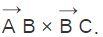 Finally, we have the below expression to derive the equation of the plane.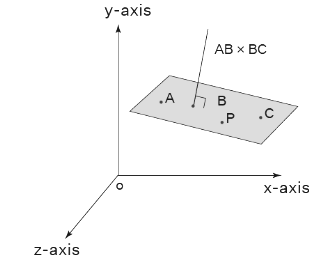  

Equation of a plane passing through the Intersection of Two Given Planes.

The given two equations of a plane are 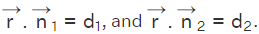 The position vector of any point on the line of intersection of these two planes must satisfy both the equations of the planes. If  is the position vector of any point on the line of intersection of these two planes, then we have 

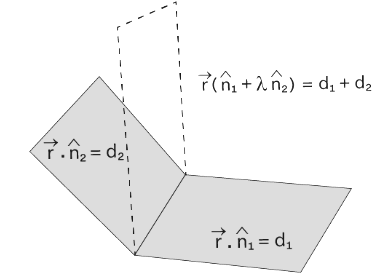
For any real values of a constant λ, we have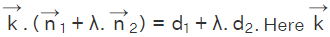  

is arbitrary and can be replaced with r to obtain the required equation of the plane. Thus the equation of the plane passing through the line of intersection of the two plane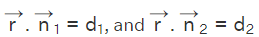s  is 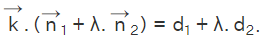 Further this equation can be solved for λ, to obtain the required equation of the Plane.

Cartesian Form of Equation of Plane

The equation of a plane in vector form can easily be transformed into cartesian form by presenting the values of each of the vectors in the equation.

Equation of Plane in Normal Form

The vector form of equation of a plane is 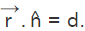 Here let us substitute  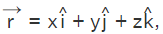and the unit normal vector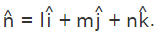 

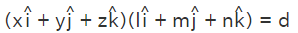
lx + my + nk = d
lx + my + nk = d is the required cartesian form of equation of a line. 

Equation of a Plane Perpendicular to a given vector and through a Point

The vector form of equation of a plane is 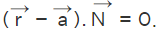 Here we take 
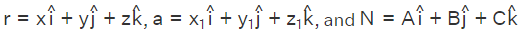 respectively. Substituting these in the vector form of the equation of the line we have the following expression. 

Equation of a Plane Passing Through Three Non-Collinear Points

The equation of plane passing through three noncollinear points A, B, C, having the position vectors as 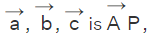 and the perpendicular   Here we take 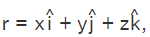 and the points as A(x1,y1,z1)(�1,�1,�1), B(x2,y2.z2)(�2,�2.�2), and C(x3,y3,z3)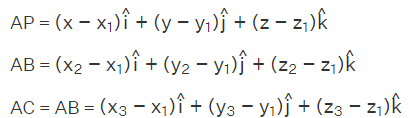(�3,�3,�3). 

Substituting these in the above equation of the plane we have the following cartesian form of equation of plane.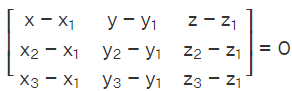 

Equation of a plane passing through the Intersection of Two Given Planes

The equation of a plane passing through the intersection of two planes  To convert this equation of plane in cartesian form let us take 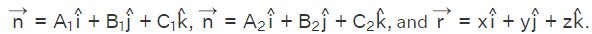 Substituting these vectors in the above equation of a plane, we have the following expression. x(A1+λA2)+y(B1+λB2)+z(C1+λC2)=d1+λd2�(�1+λ�2)+�(�1+λ�2)+�(�1+λ�2)=�1+λ�2 (A1x+B1y+C1z−d1)+λ(A2x+B2y+C2z−d2)=0(�1�+�1�+�1�−�1)+λ(�2�+�2�+�2�−�2)=0