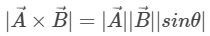Cross Product (Vector Product) - Definition, Formula and Examples - JEE PDF Download

What is a Cross Product?

Cross product is a binary operation on two vectors in three-dimensional space. It results in a vector that is perpendicular to both vectors. The Vector product of two vectors, a and b, is denoted by a × b. Its resultant vector is perpendicular to a and b. Vector products are also called cross products. Cross product of two vectors will give the resultant a vector and calculated using the Right-hand Rule.

Cross Product of Two Vectors

The vector product or cross product of two vectors A and B is denoted by A × B, and its resultant vector is perpendicular to the vectors A and B. The cross product is mostly used to determine the vector, which is perpendicular to the plane surface spanned by two vectors, whereas the dot product is used to find the angle between two vectors or the length of the vector. The cross product of two vectors, say A × B, is equal to another vector at right angles to both, and it happens in the three dimensions.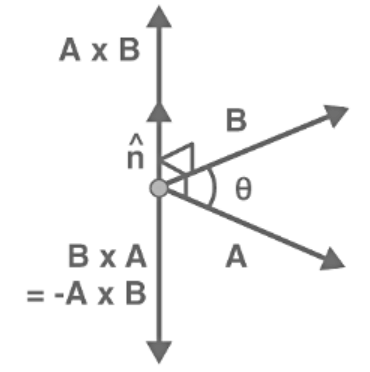

Cross Product Formula

If θ is the angle between the given two vectors A and B, then the formula for the cross product of vectors is given by:
A × B =|A| |B| sin θ Or,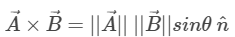

Here,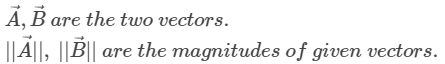 

Cross product of two vectors Formula

Consider two vectors,
A = ai + bj + ck
B = xi + yj + zk
We know that the standard basis vectors i, j, and k satisfy the below-given equalities.
i × j = k and j × i = -k j × k = i and k × j = -i k × i = j and i × k = -j
Also, the anti-commutativity of the cross product and the distinct absence of linear independence of these vectors signifies that:
i × i = j × j = k × k = 0
Now,
A × B = (ai + bj + ck) × (xi + yj + zk)
= ax(i × i) + ay(i × j) + az(i × k) + bx(j × i) + by(j × j) + bz(j × k) + cx(k × i) + cy(k × j) + cz(k × k)
By applying the above-mentioned equalities,
A × B = ax(0) + ay(k) + az(-j) + bx(-k) + by(0) + bz(i) + cx(j) + cy(-i) + cz(0) = (bz – cy)i + (cx – az)j + (ay – bx)k

Cross Product Matrix

We can also derive the formula for the cross product of two vectors using the determinant of the matrix as given below.
A = ai + bj + ck B = xi + yj + zk
Thus,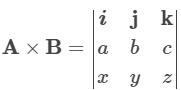

A × B = (bz – cy)i – (az – cx)j + (ay – bx)k = (bz – cy)i + (cx – az)j + (ay – bx)k

Clear all your JEE doubts with EduRev Join for Free

Join for Free

Right-hand Rule Cross Product

We can find the direction of the unit vector with the help of the right-hand rule.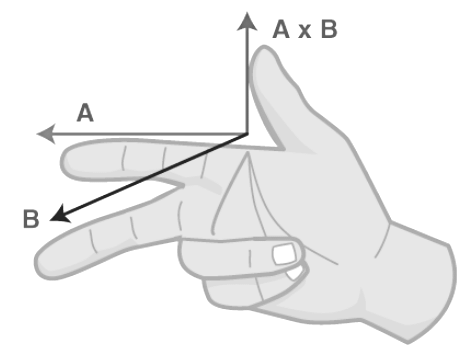

In this rule, we can stretch our right hand so that the index finger of the right hand is in the direction of the first vector and the middle finger is in the direction of the second vector. Then, the thumb of the right hand indicates the direction or unit vector n. With the help of the right-hand rule, we can easily show that vectors’ cross product is not commutative. If we have two vectors  A  and B, then the diagram for the right-hand rule is as follows:

Cross Product Properties

To find the cross product of two vectors, we can use properties. The properties such as anti-commutative property, zero vector property plays an essential role in finding the cross product of two vectors. Apart from these properties, some other properties include Jacobi property, distributive property. The properties of cross-product are given below: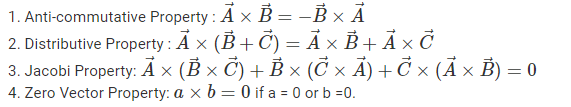

Cross Product of Perpendicular Vectors

Cross product of two vectors is equal to the product of their magnitude, which represents the area of a rectangle with sides X and Y. If two vectors are perpendicular to each other, then the cross product formula becomes:θ = 90 degrees We know that, sin 90° = 1.
So, 

Download the notes Cross Product (Vector Product) - Definition, Formula and Examples

Download as PDF

Download as PDF

Cross Product of Parallel vectors

The cross product of two vectors are zero vectors if both the vectors are parallel or opposite to each other. Conversely, if two vectors are parallel or opposite to each other, then their product is a zero vector. Two vectors have the same sense of direction.θ = 90 degrees As we know, sin 0° = 0 and sin 90° = 1.
So,

Take a Practice Test Test yourself on topics from JEE exam

Practice Now

Practice Now

Magnitude of Cross Product

Let us assume two vectors,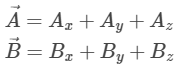

Then the magnitude of two vectors is given by the formula,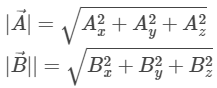

Hence, the magnitude of the cross product of two vectors is given by the formula,