Triangles Class 10 Worksheet Maths Chapter 6
Multiple Choice Questions
Q1: Which of the following triangles have the same side lengths?
(a) Scalene
(b) Isosceles
(c) Equilateral
(d) None of these
Ans: (c)
Sol: Equilateral triangles have all sides and all angles equal.
Q2: Area of an equilateral triangle with side length a is equal to:
(a) (√3/2)a
(b) (√3/2)a2
(c) (√3/4) a2
(d) (√3/4) a
Ans: (c)
Sol: Area of an equilateral triangle with side length a = √3/4 a2
Q3: D and E are the midpoints of side AB and AC of a triangle ABC, respectively, and BC = 6 cm. If DE || BC, then the length (in cm) of DE is:
(a) 2.5
(b) 3
(c) 5
(d) 6
Ans: (b)
Sol: By midpoint theorem, DE = ½ BC;
DE = ½ of 6; DE = 3 cm
Q4: The diagonals of a rhombus are 16 cm and 12 cm, in length. The side of the rhombus in length is:
(a) 20 cm
(b) 8 cm
(c) 10 cm
(d) 9 cm
Ans: (c)
Sol: Here, half of the diagonals of a rhombus are the sides of the triangle, and the side of the rhombus is the hypotenuse.
By Pythagoras theorem,
(16/2)2 + (12/2)2 = side2
82 + 62 = side2
side = 10 cm
Q5: Corresponding sides of two similar triangles are in the ratio of 2:3. If the area of the small triangle is 48 sq.cm, then the area of the large triangle is:
(a) 230 sq.cm.
(b) 106 sq.cm
(c) 107 sq.cm.
(d) 108 sq.cm
Ans: (d)
Sol: Let A1 and A2 be the areas of the small and large triangles.
Then,
A2/A1 = (side of large triangle/side of small triangle);
A2/48 = (3/2)2
A2 = 108 sq.cm.
Q6: If the perimeter of a triangle is 100 cm and the length of two sides are 30 cm and 40 cm, the length of the third side will be:
(a) 30 cm
(b) 40 cm
(c) 50 cm
(d) 60 cm
Ans: (a)
Sol: Perimeter of the triangle = sum of all its sides;
P = 30 + 40 + x
100 = 70 + x
x = 30 cm
Q7: If triangles ABC and DEF are similar and AB = 4 cm, DE = 6 cm, EF = 9 cm, and FD = 12 cm, the perimeter of triangle ABC is:
(a) 22 cm
(b) 20 cm
(c) 21 cm
(d) 18 cm
Ans: (d) 18 cm
Sol: ABC ~ DEF
AB = 4 cm, DE = 6 cm, EF = 9 cm, and FD = 12 cm;
AB/DE = BC/EF = AC/DF
BC = (4.9)/6 = 6 cm
AC = (12.4)/6 = 8 cm
Perimeter of triangle ABC = AB + BC + AC
= 4 + 6 + 8 = 18 cm
Q8: The height of an equilateral triangle of side 5 cm is:
(a) 4.33 cm
(b) 3.9 cm
(c) 5 cm
(d) 4 cm
Ans: (a)
Sol: The height of the equilateral triangle ABC divides the base into two equal parts at point D. Therefore, BD = DC = 2.5 cm. In triangle ABD, using Pythagoras theorem,
AB2 = AD2 + BD2
52 = AD2 + 2.52
AD2 = 25 - 6.25
AD2 = 18.75
AD = 4.33 cm
Q9: If ABC and DEF are two triangles and AB/DE = BC/FD, then the two triangles are similar if
(a) ∠A = ∠F
(b) ∠B = ∠D
(c) ∠A = ∠D
(d) ∠B = ∠E
Ans: (b)
Sol: If ABC and DEF are two triangles and AB/DE=BC/FD, then the two triangles are similar if ∠B=∠D.
Q10: Sides of two similar triangles are in the ratio 4: 9. Areas of these triangles are in the ratio
(a) 2: 3
(b) 4: 9
(c) 81: 16
(d) 16: 81
Ans: (d)
Sol: Let ABC and DEF be two similar triangles, such that,
ΔABC ~ ΔDEF
and AB/DE = AC/DF = BC/EF = 4/9.
As the ratio of the areas of these triangles will be equal to the square of the ratio of the corresponding sides,
∴ Area(ΔABC)/Area(ΔDEF) = AB2/DE2
∴ Area(ΔABC)/Area(ΔDEF) = (4/9)2 = 16/81 = 16: 81
Solve the following Questions
Q1: The areas of two similar triangles ABC and PQR are in the ratio 9 : 16. If BC = 4.5 cm, find the length of QR.
Ans:
We know that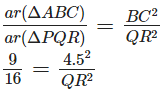
QR = 6cm
Q2: Determine whether the triangle having sides (b − 1) cm, 2√b cm and (b + 1) cm is a right angled triangle.
Ans: These are sides of the Right angle triangle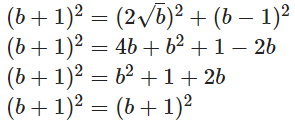
Q3: Sides of triangles are given below. Determine which of them are right triangles.In case of a right triangle, write the length of its hypotenuse.
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm,4 cm,5 cm
(iii) 40 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm
Ans: i. 252 = 72 + 242
Hence right angle triangle with 25 cm as hypotenuse
ii. 52 = 32 + 42
Hence right angle triangle with 5 cm as hypotenuse
iii. 1002 = 402 + 802
Hence right angle triangle with 100 cm as hypotenuse
iv. 132 = 122 + 52
Hence right angle triangle with 13 cm as hypotenuse
Q4: In ΔABC, AD is perpendicular to BC. Prove that:
a. AB2 + CD2 = AC2 + BD2
b. AB2 − BD2 = AC2 − CD2
Ans: In ΔABC, AD is perpendicular to BC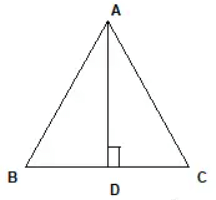
Now ΔABD is an right -angle triangle
So from Pythagoras theorem
Similarly ΔADC is an right -angle triangle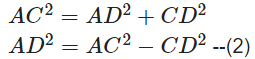
So from Pythagoras theorem
From (1) and (2)
AB2 - BD2 = AC2 - CD2
Which proved part (b)
Now rearranging,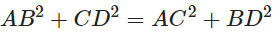
Which proved part (a).
Q5: Triangle ABC is right- angled at B and D is the mid - point of BC.
Prove that: AC2 = 4AD2 − 3AB2
Ans:
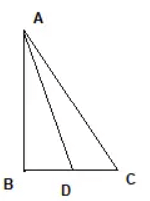
In right angle triangle ABC
AC2 = AB2 − BC2___(1)
In right triangle ABD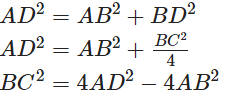
Substituting this in equation (1)
AC2 = 4AD2 − 3AB2
Q6: ABC is an isosceles triangle, right -angled at C. Prove that AB2 = 2BC2 .
Ans:
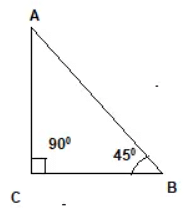
Now Since it is an isosceles triangle
AC=BC -(1)
Now from Pythagorean theorem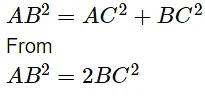
Q7: A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Ans: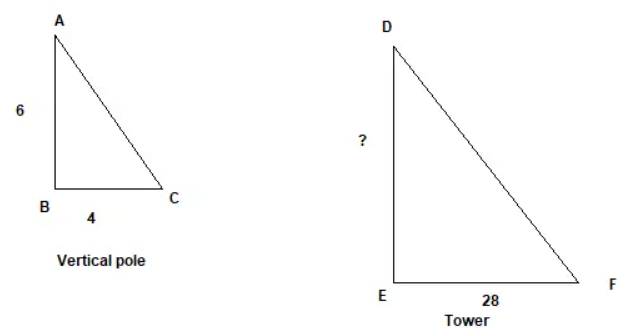
AB = 6m
BC= 4 m
Let Height of tower (DE)=h m
EF = 28 m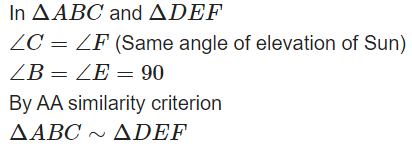
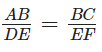
h = 42m
Q8: The foot of a ladder is 6 m away from a wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its tip reach?
Ans: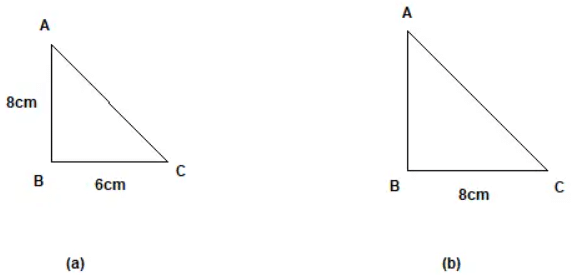
First case is depicted in the figure (a)
Now from Pythagoras theorem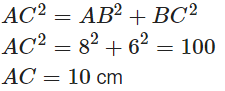
This is the length of the ladder.
Now Second case is depicted in figure (b)
AC=10 cm
BC=8 cm
Now from Pythagoras theorem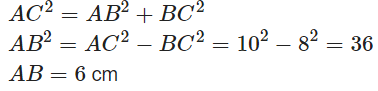
Q9: The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, find the corresponding median of the other.
Ans: We know that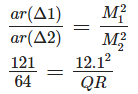
QR = 8.8 cm
Q10: DEF is an equilateral triangle of side 2b. Find each of its altitudes.
Ans: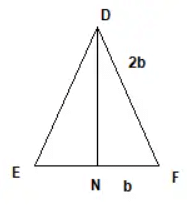
In right angle triangle DNF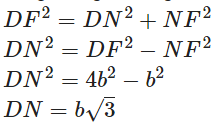
|
127 videos|550 docs|75 tests
|
FAQs on Triangles Class 10 Worksheet Maths Chapter 6
| 1. What are the different types of triangles? |  |
| 2. How do you determine the area of a triangle? |  |
| 3. What is the Pythagorean theorem? |  |
| 4. How do you find the perimeter of a triangle? |  |
| 5. Can all angles of a triangle be acute? |  |























