Class 10 Maths Chapter 8 Question Answers - Introduction to Trigonometry
Q1: In the adjoining figure, ABCD is a rectanlge with breadth BC = 7 cm and ∠CAB = 30°. Find the length of side AB of the rectangle and length of diagonal AC. If the ∠CAB = 60°, then what is the size of the side AB of the rectangle. [Use √3 = 1.73 and √2 = 1.41, if required)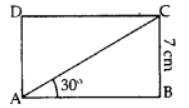 Ans:
Ans:
Case (i): ∠CAB = 30°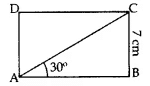 In right ΔABC:
In right ΔABC:
tan 30° = BCAB
1√3 = 7AB
AB = 7√3 ⇒ AB = 7 × 1.73 = 12.11 cm
In right ΔABC:
sin 30° = BCAC
12 = 7AC
AC = 14 cm
Case (ii): ∠CAB = 60° In right ΔABC:
In right ΔABC:
tan 60° = BCAB
√3 = 7AB
AB = 7√3
AB = 7√3 × √3√3 = 7√33
AB = 73 × 1.73 = 12.113 ≈ 4.036 cm
Q2: Prove that: 1 − tan θ + sin³θsin θ − cos θ = 1 + sin θ cos θ
Ans:
L.H.S.
= cos²θ1 − tan θ + sin³θsin θ − cos θ
= cos²θ1 − sin θcos θ + sin³θsin θ − cos θ
= cos²θ(cos θ − sin θ) + sin³θ(sin θ − cos θ)
= cos³θcos θ − sin θ + sin³θcos θ − sin θ
= cos³θ − sin³θcos θ − sin θ
= (cos θ − sin θ)(cos²θ + sin²θ + cos θ sin θ)cos θ − sin θ
= cos²θ + sin²θ + cos θ sin θ
= 1 + sin θ cos θ [∵ cos²θ + sin²θ = 1]
= R.H.S.
Q3: If x = r sin A cos C, y = r sin A sin C and z = r cos A, then prove that x2 + y2 + z2 = r2.
Ans:
x = r sin A cos C; y = r sin A sin C; z = r cos A
Squaring and adding,
L.H.S. x2 + y2 + z2 = 2 sin2 A cos2C + r2 sin2 A sin2 C + r2 cos2 A
= r2 sin2 A(cos2 C + sin2 C) + r2 cos2 A
= r2 sin2 A + r2 cos2 A … [cos2θ + sin2θ = 1
= r2 (sin2 A + cos2 A) = r2 = R.H.S.
Q4: Prove that: (cot A + sec B)2 – (tan B – cosec A)2 = 2(cot A . sec B + tan B. cosec A)
Ans:
L.H.S.
= (cot A + sec B)2 – (tan B – cosec A)2
= cot2 A + sec2 B + 2 cot A sec B – (tan2 B + cosec2 A – 2 tan B cosec A)
= cot2 A + sec2 B + 2 cot A sec B – tan2 B – cosec2 A + 2 tan B cosec A
= (sec2 B – tan2 B) – (cosec2 A – cot2 A) + 2(cot A sec B + tan B cosec A)
= 1 – 1 + 2(cot A sec B + tan B cosec A) … [∵ sec2B – tan2 B = 1
cosec2A – cot2 A = 1
= 2(cot A . sec B + tan B . cosec A) = R.H.S.
Q5: Prove the following trigonometric identities: sin A (1 + tan A) + cos A (1 + cot A) = sec A + cosec A.
Ans: L.H.S. = sin A (1 + tan A) + cos A (1 + cot A)
= sin A (1 + sin Acos A) + cos A (1 + cos Asin A)
= sin A (cos A + sin A)cos A + cos A (sin A + cos A)sin A
= (sin A + cos A) (sin A + cos A)cos A sin A
= (sin A + cos A)cos A sin A
= sin Asin A cos A + cos Asin A cos A
= 1cos A + 1sin A
= sec A + cosec A = R.H.S. (Hence proved)
Q6: Prove the identity: sin A + cos Asin A − cos A + sin A − cos Asin A + cos A = 21 − 2cos²A
Ans:
L.H.S.
= sin A + cos Asin A − cos A + sin A − cos Asin A + cos A
= (sin A + cos A)² + (sin A − cos A)²(sin A − cos A)(sin A + cos A)
= sin²A + cos²A + 2sin A cos A + sin²A + cos²A − 2sin A cos Asin²A − cos²A
= 1 + 11 − cos²A − cos²A
= 21 − 2cos²A
= R.H.S. (Hence proved)
Q7: Prove that: (1 + cot A + tan A)(sin A − cos A) = sec³ A − csc³ Asec² A · csc² A
Ans:
L.H.S.
= (1 + cot A + tan A)(sin A − cos A)
= (1 + cos Asin A + sin Acos A)(sin A − cos A)
= sin A cos A + cos² A + sin² Asin A cos A (sin A − cos A)
= (sin³ A − cos³ A)sin A cos A
= sin³ A − cos³ Asin³ A cos³ A
[Dividing numerator and denominator by sin³ A cos³ A]
= sec³ A − csc³ Asec² A · csc² A
= R.H.S. (Hence proved)
Q8: Prove that: √(1 + sin A)√(1 − sin A) + √(1 − sin A)√(1 + sin A) = 2 sec A = 2(sin A tan A + cos A)
Ans:
L.H.S.
= √(1 + sin A)√(1 − sin A) + √(1 − sin A)√(1 + sin A)
= (1 + sin A) + (1 − sin A)√(1 − sin² A)
= 2√(cos² A)
= 2cos A = 2 sec A ...(i)
R.H.S.
= 2(sin A tan A + cos A)
= 2 sin Acos A + 2 cos A
= 2 sin² A + cos² Acos A
= 2 1cos A = 2 sec A ...(ii)
From (i) and (ii),
L.H.S. = R.H.S.
Hence proved: √(1 + sin A)√(1 − sin A) + √(1 − sin A)√(1 + sin A) = 2 sec A = 2(sin A tan A + cos A)
Q9: Find the value of: sin θsec θ + tan θ − 1 + cos θcosec θ + cot θ − 1 = 1
Ans:
= sin θsec θ + tan θ − 1 + cos θcosec θ + cot θ − 1
= sin θ1/cos θ + sin θ/cos θ − 1 + cos θ1/sin θ + cos θ/sin θ − 1
= sin θ1 + sin θ − cos θ + cos θ1 + cos θ − sin θ
= sin θ cos θ(1 + sin θ − cos θ)(1 + cos θ − sin θ)
= 21 − 2 sin θ cos θ [Using simplifications and identities]
= 22 sin θ cos θ = 1
Hence proved.
Q10: Prove that: √(sec A - 1)√(sec A + 1) + √(sec A + 1)√(sec A - 1) = 2 cosec A
Ans:
L.H.S.
= √(sec A - 1)√(sec A + 1) + √(sec A + 1)√(sec A - 1)
= sec A - 1 + sec A + 1√(sec² A - 1)
= 2 sec A√(tan² A)
= 2 sec Atan A
= 2sin A
= 2 cosec A
= R.H.S. (Hence proved)
|
127 videos|551 docs|75 tests
|
FAQs on Class 10 Maths Chapter 8 Question Answers - Introduction to Trigonometry
| 1. What is trigonometry and why is it important in Class 10 mathematics? |  |
| 2. How do we find the values of trigonometric ratios in Class 10? |  |
| 3. What are the basic trigonometric ratios and how are they used in Class 10? |  |
| 4. How can trigonometry be applied in real-life situations? |  |
| 5. What are the practical applications of trigonometry in Class 10 mathematics? |  |





















