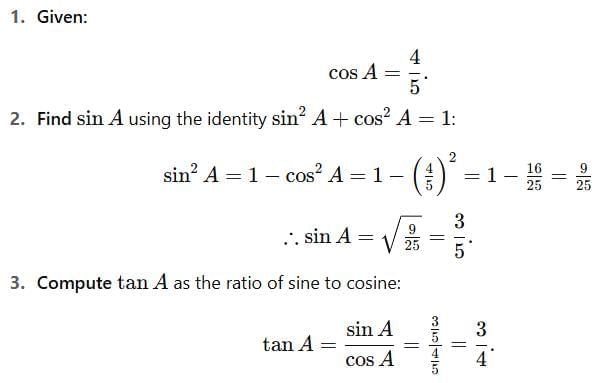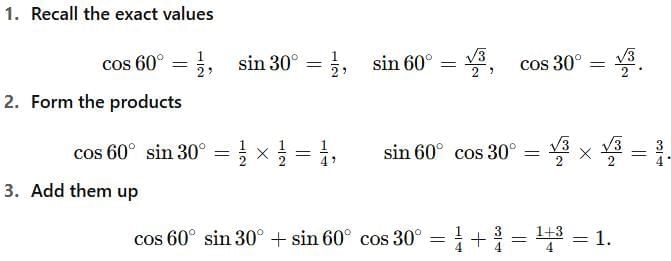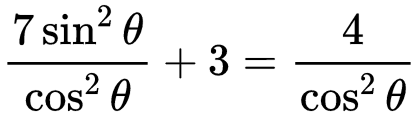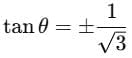Unit Test (Solutions): Introduction to Trigonometry | Mathematics (Maths) Class 10 PDF Download
Time: 1 hour
M.M. 30
Attempt all questions.
- Question numbers 1 to 5 carry 1 mark each.
- Question numbers 6 to 8 carry 2 marks each.
- Question numbers 9 to 11 carry 3 marks each.
- Question number 12 & 13 carry 5 marks each.
Q1: When cos A = 4/5, the value for tan A is (1 Mark)
(a) 3/5
(b) 3/4
(c) 5/3
(d) 4/3
Ans: (b) 3/4
Q2: Which of the following is the the simplest value of cos² θsin θ + sin θ (1 Mark)
(a) cosec θ
(b) sec θ
(c) sin θ
(d) cos θ
Ans: (a) cosec θ
Sol: cos² θ + sin² θsin θ = 1sin θ = cosec θ
Q3: Evaluate cos 60° sin 30° + sin 60° cos 30° (1 Mark)
(a) 1
(b) 3
(c) 1/2
(d) 3/2
Ans: (a) 1,
Q4: If cos A = 2/5, find the value of 4 + 4 tan2A
(a) 5
(b) 1/25
(c) 25
(d) 1/5
Ans: (d) 25
Q5: What is the value of (cos2 67° – sin2 23°) (1 Mark)
(a) 2
(b) 0
(c) 6
(d) 1
Ans: (b) 0
67° + 23° = 90°
∴ cos2 67° – sin2 23° = cos2 (90° – 23°) – sin223°
= sin2 23° – sin2 23°
= 0
Q6: Find the value of sin 38° – cos 52°? (2 Mark)
Ans:
sin 38° – cos 52°
= sin38° – cos (90° – 38°) [∵ cos (90° – θ = sin θ]
= sin 38° – sin 38°
= 0
Q7: Prove the following : (2 Mark)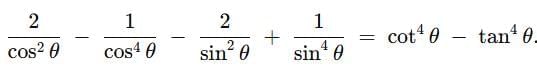
Ans:
Here 1cos θ = sec θ and 1sin θ = cosec θ
LHS = 2cos² θ - 1cos⁴ θ - 2sin² θ + 1sin⁴ θ
= 2 sec² θ - sec⁴ θ - 2 cosec² θ + cosec⁴ θ
= 2(1 + tan² θ) - (1 + tan² θ)² - 2(1 + cot² θ) + (1 + cot² θ)²
= (1 + tan² θ)(2 - (1 + tan² θ)) - (1 + cot² θ)(2 - (1 + cot² θ))
= (1 + tan² θ)(1 - tan² θ) - (1 + cot² θ)(1 - cot² θ)
= 1 - tan⁴ θ - (1 - cot⁴ θ) = cot⁴ θ - tan⁴ θ
Hence proved
Q8: If 7sin2θ + 3cos2θ = 4, then find the value of tan θ. (2 Marks)
Ans:
7sin2θ + 3cos2θ = 4
Dividing both sides by cos2θ
7tan2θ + 3 = 4sec2θ
= 4(1 + tan2θ)
⇒ 3tan2θ = 1
Q9: When sec 4A = cosec (A – 20°), here 4A is an acute angle, find out the value of A. (3 Marks)
Ans: sec 4A = cosec (A – 20°)
We get that sec 4A = cosec (90° – 4A)
To find out the value of A, thus, substitute the above equation in a given problem
cosec (90° – 4A) = cosec (A – 20°)
then, equate the angles
90° – 4A= A- 20°
110° = 5A
A = 110°/ 5 = 22°
Hence, the value of A = 22°
Q10: If 3x = sec θ and 9 x² - 1x² = tan θ, then find the value. (3 Marks)
Ans:
9 x² - 1x² = 9 (sec θ)²3 - (tan θ)²3
= 9 sec² θ - tan² θ3
= 9 × 13 = sec² θ - tan² θ
= 1
Q11: If ∠A and ∠B are the acute angles such that cos A = cos B, then show that ∠ A = ∠ B. (3 Marks)
Ans: Let us assume that the triangle ABC in which CD⊥AB
Given that the angles A and B are acute angles, such that
Cos (A) = cos (B)
As per the angles taken, the cost ratio is written as
AD/AC = BD/BC
Now, interchange the terms, we get
AD/BD = AC/BC
Let take a constant value, AD/BD = AC/BC = k
then consider the equation as
AD = k BD …(1)
AC = k BC …(2)
By applying the Pythagoras theorem in △CAD and △CBD we get,
CD2 = BC2 – BD2 … (3)
CD2 =AC2 −AD2 ….(4)
From the equations (3) and (4) we observe,
AC2 − AD2 = BC2 − BD2
then substitute the equations (1) and (2) in (3) and (4)
k2(BC2−BD2) = (BC2−BD2) k2 = 1
Putting this value in equation, we obtain that
AC = BC
∠A=∠B (Angles opposite to the equal side are equal-isosceles triangle)
Q12: In triangle ABC, right-angled at B, when tan A = 1/√3 find out the value : (5 marks)
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Ans:
Let’s ΔABC in which ∠B=90°
tan A = BC/AB = 1/√3
Let’s BC = 1k and AB = √3 k,
here k is the positive real number of the problem
By the Pythagoras theorem in ΔABC we get:
AC2 = AB2 + BC2
AC2 = (√3 k)2 + (k)2
AC2 = 3k2 + k2
AC2 = 4k2
AC = 2k
then find the values of cos A, Sin A
Sin A = BC/AC = 1/2
Cos A = AB/AC = √3/2
now, find the values of cos C and sin C
Sin C = AB/AC = √3/2
Cos C = BC/AC = 1/2
then, substitute the values in the given problems
(i) sin A cos C + cos A sin C
= (1/2) ×(1/2 )+ √3/2 ×√3/2
= 1/4 + 3/4
= 1(ii) cos A cos C – sin A sin C
= (√3/2 )(1/2) – (1/2) (√3/2 )
= 0
Q13: In ∆ ABC, the right-angled at B, AB = 24 cm, BC = 7 cm. Determine: (5 Marks)
(i) sin A, cos A
(ii) sin C, cos C
Ans:
In the given triangle ABC, right angled at B = ∠B = 90°
Given: AB = 24 cm as well as BC = 7 cm
According to the Pythagoras Theorem,
In the right-angled triangle, the squares of the hypotenuse sides are equal to the addition of the squares for the other two sides.
On applying the Pythagoras theorem, we observe
AC2 = AB2 + BC2
AC2 = (24)2 + 72
AC2 = (576+49)
AC2 = 625cm2
AC = √625 = 25
thus, AC = 25 cm
(i) To find Sin (A), Cos (A)
We get that sine (or) Sin function is equal to the ratio of length of the opposite sides to the hypotenuse sides. So it becomes
Sin (A) = Opposite side /Hypotenuse side = BC/AC = 7/25
Cosine or Cos function is same as the ratio of the length of the adjacent side to the hypotenuse side so it becomes,
Cos (A) = Adjacent side/Hypotenuse side = AB/AC = 24/25
(ii) To find out Sin (C), Cos (C)
Sin (C) = AB/AC = 24/25
Cos (C) = BC/AC = 7/25
|
127 videos|584 docs|79 tests
|
FAQs on Unit Test (Solutions): Introduction to Trigonometry - Mathematics (Maths) Class 10
| 1. What are the basic trigonometric ratios and how are they defined in a right-angled triangle? |  |
| 2. How do you find the values of trigonometric ratios for commonly used angles like 0°, 30°, 45°, 60°, and 90°? |  |
| 3. What is the Pythagorean theorem and how does it relate to trigonometry? |  |
| 4. What are trigonometric identities and can you provide examples? |  |
| 5. How can trigonometry be applied in real-life situations? |  |