Class 9 Science Chapter 10 Question Answers - Work and Energy
Q1: A force of 10N causes a displacement of 2 m in a body in its own direction. Calculate the work done by force.
Ans:
The work done by force = F × s
= 10 N × 2 m
= 20 J
Q2: How much force is applied on the body when 150 joule of work is done in displacing the body through a distance of 10 m in the direction of force?
Ans:
W = F × s
F = W/s
= 150 /10
= 15N
Q3: A body of 5 kg raised to 2 m find the work done.
Ans:
The work done to raise a body = PE
= mgh
= 5 kg × 9.8 × 2
= 98 joule
Q4: A work of 4900 J is done on load of mass 50 kg to lift it to a certain height. Calculate the height through which the load is lifted.
Ans:
Work done on road to lift = mgh
4900 = 50 × 9.8 h
h = 10 m
Q5: An engine work 54,000 J work by exerting a force of 6000 N on it. What is the displacement of the force?
Ans:
S = W/F
= 54000J / 6000 N
= 9m
Q6: A body of mass 2 kg is moving with a speed of 20 m/s. Find the kinetic energy.
Ans:
KE = 0.5 mv2
= 0.5 × 2 × 20 × 20
= 400 J
Q7: A hammer of mass 1 kg falls freely from a height of 2 m. Calculate (I) The velocity and (II) The kinetic energy of the hammer just before it touches the ground. Does the velocity of hammer depend on the mass of hammer?
Ans:
PE = mgh
= 1 × 9.8 × 2
= 19.6 J
PE = KE
= 0.5 mv2
19.6 = 0.5 × 1 × v2
39.2 = v2
v = 6.29 m/s
No, velocity of hammer does not depend on the mass of the hammer as v = u + at
Q8: A weight of 50 kg runs up a hill rising himself vertically 10 m in 20 sec. Calculate power. (Given g = 9.8 ms–1)
Ans: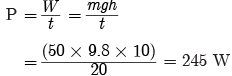
Q9: A rickshaw puller pulls the rickshaw by applying a force of 100 N. If the rickshaw moves with constant velocity of 36 kmh–1. Find the power of rickshaw puller.
Ans:
Force = 100 N
Velocity = 36 km/h
= 36 x 5 / 18
= 10 m/s
Power = Force × Velocity
Power = 100 × 10 = 1000 Watt
Therefore, power of rickshaw puller = 1000 Watt
Q10: An athlete weighing 60 kg runs up a staircase having 10 steps each of 1 m in 30 sec. Calculate power (g = 9.8ms–1).
Ans:
h = 10 × 1m = 10 m
Work done = potential energy
= mgh
= 60 × 9.8 × 10
= 5880 J
Power = W/t = 5880 / 30 = 196 W
Q11: A horse exert a force of 200N to pull the cart. If the horse cart system moves with velocity 36 kmh–1 on the level road, then find the power of horse in term of horse power (1 HP = 746 W).
Ans:
Velocity = 36 kmh–1 = 10 m/s
W =F × s = 200 × 10 = 2000J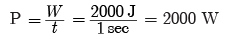
746 W = 1 HP
So, 2000 W = 2000/746
= 2.68 HP
Q12: An electric kettle of 500W is used to heat water everyday for 2 hours. Calculate the number of unit of electrical energy consumed by it in 10 days
Ans:
E = Pt = 500 W × 10 × 2h
= 10000 Wh
= 10 kWh
= 10 unit
Q13: Calculate the cost of using a 2 kWh immersion rod for heating water in a house for one hour each day for 60 days if the rate is 1.50 per unit kWh.
Ans:
E = Pt = 2 kW × 60 × 1 h
= 120 kWh = 120 unit
The cost of using a 2 kWh immersion rod for heating water = 120 × 1.5 = Rs 180
Q14: In an experiment to measure his power, a student records the time taken by him in running up a flight of steps on a staircase.
Ans:
Use the following data to calculate the power of the student :
Number of steps = 28,
Height of each step = 20 cm,
Time taken = 5.4 s,
Mass of student = 55 kg,
Acceleration due to gravity = 9.8 ms–2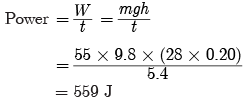
Q15: The power of a heart which beats 72 times in a minute is 1.2 kW. Calculate the work done by heart for each beat. (1 kJ)
Ans:
P = 1200 W and t = 60 s
W = P × t = 1200 × 60 = 72000J
In 72 times heartbeats 72000 J energy used
In one beat = 72000 / 72 = 1000J
Work done by the heart in every beat is 1 KJ.
Q16: Calculate the electricity bill amount for a month of 31 days, if the following devices are used as specified.
(a) 3 bulbs of 40 W for 6 hours.
(b) 4 tubelights of 50 W for 8 hours,
(c) A TV of 120 W for 6 hours.
The rate of electricity is Rs 2.50 per unit.
Ans:
E1 = P × t = 0.04 × 6 × 3
= 0.72 kWh
E2 = P × t = 0.05 × 8 × 4
= 1.60 kWh
E3 = 0.12 × 6 = 0.72 kWh
Total E = 0.72 + 1.6 + 0.72 = 3.04 kWh
Cost in 31 days = rate × E
= 3.04 × 2.50 × 31
= Rs 235.60
Q17: (a) What is meant by mechanical energy? State its two forms. State the law of conservation of energy. Give an example in which we observe a continuous change of one form of energy into another and vice-versa.
(b) Calculate the amount of work required to stop a car of 1000 kg moving with a speed of 72 km/h.
Ans:
(a) It is the sum of KE and PE of an object. It states that energy can neither be created nor be destroyed. We observe a continuous change in energy in a simple pendulum. At the mean position, the energy is totally kinetic while at the extreme position it is totally potential. As the pendulum oscillates its energy continuously changes between kinetic and potential.
(b) Given m = 1000 kg, u = 72 kmh–1 = 20 ms-1, v = 0
Work done = change in kinetic energy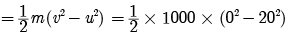
= – 200000 J = – 2 × 105 J
|
84 videos|478 docs|60 tests
|






















