Triangles Class 9 Worksheet Maths Chapter 6
Multiple Choice Questions
Q1: If AD = BC and ∠ BAD = ∠ ABC, then ∠ ACB is equal to
(a) ∠ABD
(b) ∠ BAD
(c) ∠BAC
(d) ∠BDA
Q2: If O is a midpoint of AB and ∠BQO = ∠APO, then ∠OAP is equal to
(a) ∠QPA
(b) ∠OQB
(c) ∠QBO
(d) ∠BOQ
Q3: If △ABC is an isosceles triangle, ∠ B = 65º, AB = AC,∠ B = 65º, then find ∠ A.
(a) 60º
(b) 70º
(c) 50º
(d) none of these
Q4: An angle is 14º more than its complement. Find its measure.
(a) 42º
(b) 32º
(c) 52º
(d) 62º
Q5: If ABCD is a quadrilateral where AD= CB, AB=CD, and ∠ D= ∠ B, then ∠CAB is equal to
(a) ∠ACD
(b) ∠CAD
(c) ∠ACD
(d) ∠BAD
Q6: If AB ⊥BC and ∠A =∠C, then the correct statement will
(a) AB ≠ AC
(b) AB = BC
(c) AB = AD
(d) AB = AC
Q7: If AB = AC and ∠ ACD = 120º, find ∠A.
(a) 50º
(b) 60º
(c) 70º
(d) None of these
Answer the following questions
Q1: AD and BC are equal perpendiculars to a line segment AB. Show that CD bisects AB.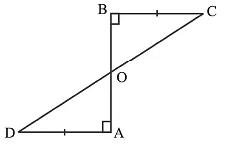
Q2: AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB. Show that
(i) ΔDAP ≌ ΔEBP
(ii) AD = BE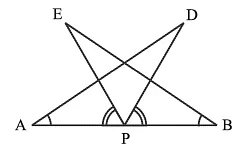
Q3: In an isosceles triangle ABC with AB = AC, D and E are points on BC such that BE = CD. Show that AD = AE.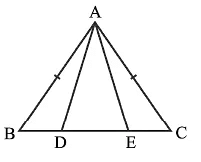
Q4: In Figure OA = OB and OD = OC.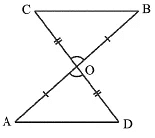 Show that
Show that
(i) ΔAOD ≅ ΔBOC
(ii) AD || BC
Q5: In Fig, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.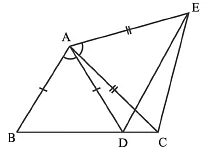
Q6: In ΔABC, the bisector AD of ∠A is perpendicular to side BC. Show that AB = AC and ΔABC is isosceles.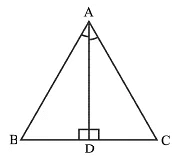
Q7: ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal. Show that
(i) ΔABE ≌ ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle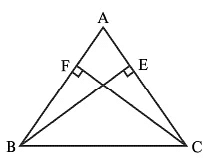
The solutions of the worksheet "Worksheet Solutions: Triangles"
|
40 videos|471 docs|57 tests
|
FAQs on Triangles Class 9 Worksheet Maths Chapter 6
| 1. What are the different types of triangles? |  |
| 2. How can we determine the type of triangle based on its angles? |  |
| 3. What is the Pythagorean Theorem and how is it used to find the length of a side in a right triangle? |  |
| 4. How can we determine the type of triangle based on its sides? |  |
| 5. How can we calculate the area of a triangle? |  |

















