Pair of Linear equations in Two Variables Class 10 Notes Maths Chapter 3
| Table of contents |

|
| What are Pair of Linear Equations in Two Variables? |

|
| Graphical Method |

|
| Algebraic Methods |

|
| Consistency of System |

|
What are Pair of Linear Equations in Two Variables?
- General form of a linear equation is given by ax + by + c = 0.
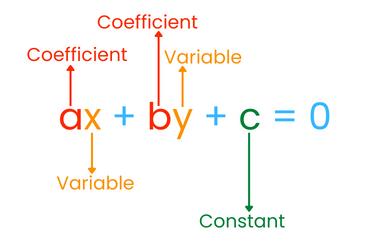
- For any linear equation, each solution (x, y) corresponds to a point on the line.
- The graph of a linear equation is a straight line.
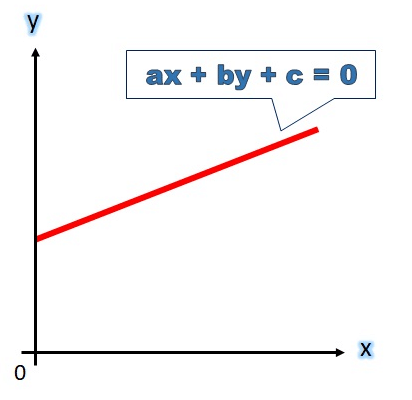
- Two linear equations in the same two variables are called a pair of linear equations in two variables.
- The most general form of a pair of linear equations is:
- A pair of values of variables ‘x‘ and ‘y’ which satisfy both the equations in the given system of equations is said to be a solution of the simultaneous pair of linear equations.
Methods to solve a Pair of Linear Equations in Two Variables
A pair of linear equations in two variables can be represented and solved, by
(i) Graphical method
(ii) Algebraic method
Graphical Method
The procedure of solving a system of linear equations by drawing the graph is known as the graphical method.
To solve a pair of linear equations in two variables graphically we follow the following steps:
Step 1. Get the given system of linear equations in two variables.
Step 2. Plot the graph of the first equation and then the second equation on the same coordinate system.
Example: Consider two linear equations, y = x -1 and y =2x + 2. Sove these equations with graphical method.
Sol: Let's graph both of these equations on the same set of axes:
Equation 1: y = x -1
For this equation, you can create a table of values and plot some points to draw the line.
| x | 0 | 1 |
| y | -1 | 0 |
Equation 2: y =2x + 2
Again, create a table of values and plot some points:
| x | 0 | 1 |
| y | 2 | 4 |
Now, you can plot these points and draw the lines.
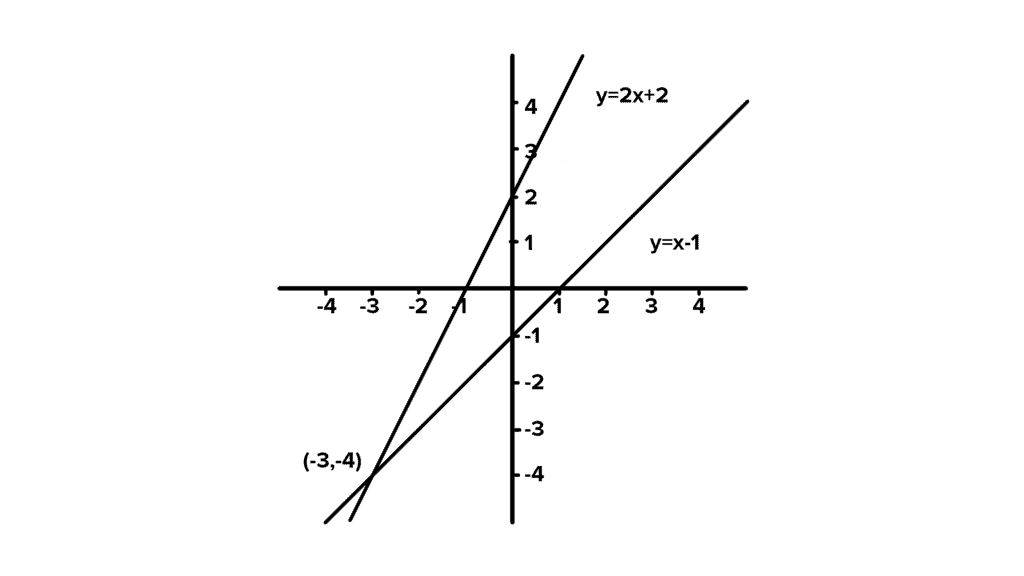
From the graph, we can see the two linear equations intersect at the common point
(-3, -4), which is the solution for the given system of linear equations.
Algebraic Methods
Following are the methods for finding the solutions(s) of a pair of linear equations:
Substitution Method
The substitution method can be defined as a way to solve a linear system algebraically. The substitution method works by substituting one y-value with the other. To put it simply, the method involves finding the value of the x-variable in terms of the y-variable.
The method of substitution involves three steps:
Step 1: First you need to solve one equation for one of the variables.
Step 2: Now you need to substitute (plug-in) this expression into the other equation and solve it.
Step 3: In the last step you need to re-substitute the value into the original equation and you will be able to find the corresponding variable.
Example: Solve for the values of ‘x’ and ‘y’: x + y = 5 and 3x + y = 11
Sol: Let’s write down the information given,
x + y = 5 …………… Equation (i)
3x + y = 11 …………Equation (ii)
Now let us try to solve them using the method of substitution:
From the first equation we find that we can write y = 5 - x.
Substituting the value of y in the Equation (ii),
we get:
3x + (5 – x) = 11⇒2x = 11 - 5⇒ 2x = 6⇒ x = 6/2.
Therefore, the value of x = 3.
Now substituting the value x = 3 in the other equation that is y = 5 – x,
we get:
y = 5- x
⇒y = 5 - 3
Therefore, we get the value of y = 2.
Hence, the value of x = 3 and the value of y = 2
Elimination Method
The elimination method is one of the most commonly used methods when it comes to solving an equation. You can eliminate one variable so you can solve the equation with ease. It is also called the addition method.
Let’s look at how equations can be solved through the elimination method math step by step.
Step 1: The first step is to multiply both the linear equations by a constant on a non-zero value. This would make the coefficients of either of the variables, x or y, numerically equal.
Step 2: The next step is adding or subtracting one equation from the other in a way that one of the variables is easily eliminated. Once you get an equation with one variable, follow the next steps. If you do not get this, then there can be two possibilities:
- If you get a true statement with no variable, then it means that the original equations have infinite solutions.
- If you get a false statement with no variable, then it means that the original equations do not have any solution and are inconsistent.
Step 3: The next step is solving the equation with one variable, either x or y, and you would get the value of that specific value.
Step 4: substituting this value in the previous equation, you would get the value of the other variable as well.
This will help you to solve the elimination method problems.
Example: Solve this set of equations 2x + y = -4 and 5x – 3y = 1 using elimination method.
Sol: The equations given are: 2x + y = -4 …………… (i)
5x – 3y = 1 …………… (ii)
Multiplying equation (i) by 3, you get,
{2x + y = -4} …………… {× 3}
6x + 3y = -12 …………… (iii)
Adding equations (ii) and (iii), you get,
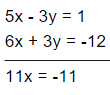
Therefore, x = -11/11
Hence, x = -1
Substituting this value of x = -1 in equation (i), you get,
2 × (-1) + y = -4
-2 + y = -4y = -4 + 2
Hence, y = -2
Therefore, x = -1 and y = -2 is the solution of the set of equations 2x + y = -4 and 5x – 3y = 1
Consistency of System
- Consistent system. A system of linear equations is said to be consistent if it has at least one solution.
- Inconsistent system. A system of linear equations is said to be inconsistent if it has no solution.
Condition for Consistency
Let the two equations be:
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
Then, 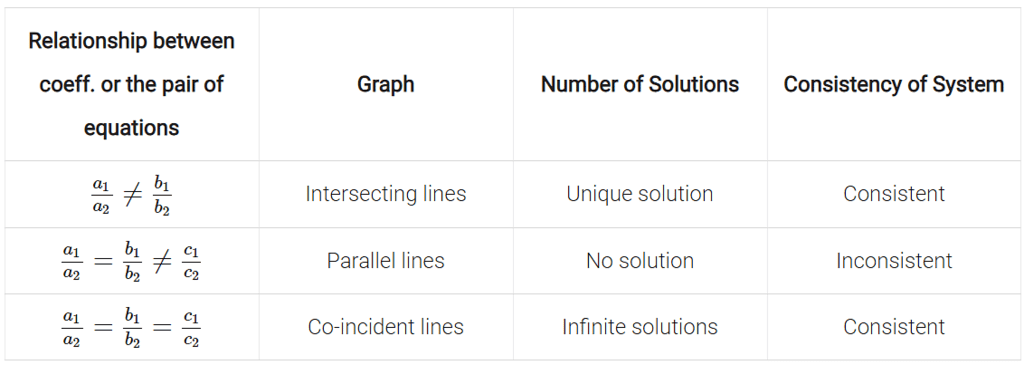
|
127 videos|674 docs|84 tests
|
FAQs on Pair of Linear equations in Two Variables Class 10 Notes Maths Chapter 3
| 1. What is the graphical method of solving a pair of linear equations in two variables? |  |
| 2. How does the substitution method work in solving a pair of linear equations in two variables? |  |
| 3. What is the elimination method for solving a pair of linear equations in two variables? |  |
| 4. How is the cross-multiplication method used to solve a pair of linear equations in two variables? |  |
| 5. How can you determine the consistency of a system of linear equations in two variables? |  |















