Quadratic Equations Class 10 Notes Maths Chapter 4
What is Quadratic Equation?
- A quadratic polynomial of the form ax2 + bx + c, where a ≠ 0 and a, b, c are real numbers, is called a quadratic equation when ax2 + bx + c = 0.
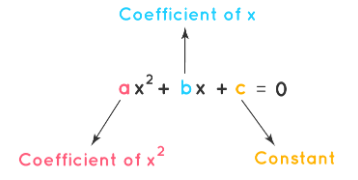
- Here a and b are the coefficients of x2 and x respectively and ‘c’ is a constant term.
- Any value is a solution of a quadratic equation if and only if it satisfies the quadratic equation.
How to Find the Solution of a Quadratic Equation by Factorisation?
For a quadratic equation, a real number α is called the root of a quadratic equation ax2 + bx + c = 0. Hence, we can write aα2 + bα + c = 0. So, x= α is the solution of a quadratic equation or the root of a quadratic equation. In other words, α satisfies the given quadratic equation.
Note: The zeros of the quadratic equation ax2+bx+c = 0 are the same as the root of the quadratic equation ax2+bx+c = 0.
Example: Solve the quadratic equation 2x2+x-300 = 0 by the factorisation method.
Solution:
Given quadratic equation: 2x2+x-300 = 0
By using factorisation, the quadratic equation 2x2 + x -300 = 0 is written as:
2x2 – 24x+25x -300 = 0
2x(x-12) +25(x-12) =0
(i.e) (x-12)(2x+25) = 0
Therefore, x-12=0 and 2x+25 = 0
x-12 = 0
Therefore, x= 12.
Similarly, 2x+25 = 0
2x= -25
x =-25/2
x = -12.5.
Hence, the roots of the quadratic equation 2x2+x-300 = 0 are 12 and -12.5.
Quadratic Formula
- The roots, if a quadratic equation ax2 + bx + c = 0 are given by:
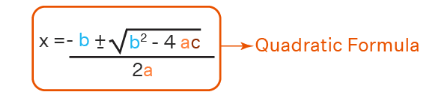
- Here, the value b2 – 4ac is known as the discriminant and is generally denoted by D. ‘D’ helps us to determine the nature of roots for a given quadratic equation. Thus D = b2 – 4ac.
Example: Find the roots of quadratic equation x2 - 7x + 10 = 0 using quadratic formula.
Solution:
Here, a = 1, b = -7 and c = 10. Then by quadratic formula:
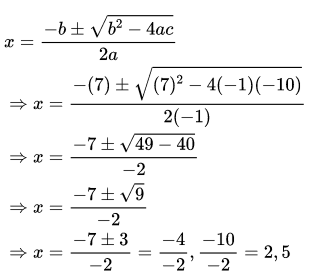
Therefore, x = 2, x = 5.
Nature of Roots of a Quadratic Equation
- If D = 0 ⇒ The roots are Real and Equal.
- If D > 0 ⇒ The two roots are Real and Unequal.
- If D < 0 ⇒ No Real roots exist.
Example: Discuss the nature of the roots of the quadratic equation 2x2 – 8x + 3 = 0.
Solution: Here the coefficients are all rational. The discriminant D of the given equation is
D = b2 – 4ac = (-8)2 – 4 x 2 x 3
= 64 – 24
= 40 > 0
Clearly, the discriminant of the given quadratic equation is positive but not a perfect square. Therefore, the roots of the given quadratic equation are real, irrational and unequal.
Relationship between roots and Coefficients of Quadratic Equation
If α and β are the roots of the quadratic equation, then Quadratic equation is
x2 – (α + β) x + αβ = 0
OR
x2 – (sum of roots) x + product of roots = 0
where,
- Sum of roots (α + β) =
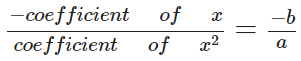
- Product of roots (α x β) =
Example: If α and β are the roots of the equation x2 - 4x + 2 = 0, find the value of
i) α2 + β2
ii) α2 - β2
iii) α3 - β3
iv)1/α + 1/ β
Solution:
The given equation is x2 - 4x + 2 = 0 ...................... (i)
According to the problem, α and β are the roots of the equation (i)
Therefore,
(i) Now α2 + β2 = (α + β)2 - 2αβ = (4)2 – 2 x 2 = 16 – 4 = 12.
(ii) α2 - β2 = (α + β)( α - β)
Now (α - β)2 = (α + β)2 - 4αβ = (4)2 – 4 x 2 = 16 – 8 = 8
⇒ α - β = ± √8
⇒ α - β = ± 2√2
Therefore, α2 - β2 = (α + β)( α - β) = 4 x (± 2√2) = ± 8√2.
(iii) α3 + β3 = (α + β)3 - 3αβ(α + β) = (4)3 – 3 x 2 x 4 = 64 – 24 = 40.
(iv) 
|
127 videos|584 docs|79 tests
|
FAQs on Quadratic Equations Class 10 Notes Maths Chapter 4
| 1. What is a quadratic equation? |  |
| 2. How can I find the solutions of a quadratic equation by factorization? |  |
| 3. What is the quadratic formula? |  |
| 4. How can I determine the nature of the roots of a quadratic equation? |  |
| 5. What is the relationship between the roots and coefficients of a quadratic equation? |  |
















