Arithmetic Progressions Class 10 Notes Maths Chapter 5
| Table of contents |

|
| What is a Sequence ? |

|
| Arithmetic Progression (A.P.) |

|
| nth term of an A.P. |

|
| Sum of n terms of an A.P. |

|
What is a Sequence ?
A sequence is an arrangement of numbers in a definite order and according to some rule.
Example:
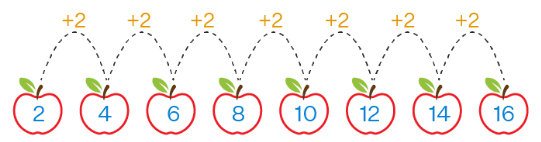
- 2, 4, 6, 8, 10, … is a sequence where each successive item is 2 greater than the preceding term.
- 1, 4, 9, 16, 25, … is a sequence where each term is the square of successive natural numbers.
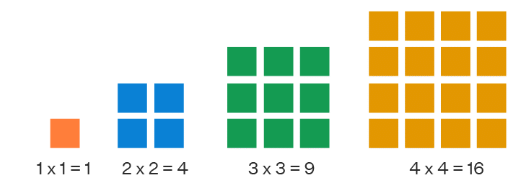
Terms
The various numbers occurring in a sequence are called ‘terms’. Since the order of a sequence is fixed, therefore the terms are known by the position they occupy in the sequence.
Example: If the sequence is defined as
Arithmetic Progression (A.P.)
An Arithmetic progression is a special case of a sequence, where the difference between a term and its preceding term is always constant, known as common difference, i.e., d. The arithmetic progression is abbreviated as A.P.
General form of an A.P.
The general form of an A.P. is
∴ a, a + d, a + 2d,… For example, 1, 9, 11, 13.., Here the common difference is 2. Hence it is an A.P.
nth term of an A.P.
In an A.P. with first term a and common difference d, the nth term (or the general term) is given by .
an = a + (n – 1)d.
where [a = first term, d = common difference, n = term number
For Example,
To find seventh term put n = 7
∴ a7 = a + (7 – 1)d or a7 = a + 6d
Solved Examples
Example 1: Find the value of n, if a = 10, d = 5, an = 95.
Sol: Given, a = 10, d = 5, an = 95
From the formula of general term, we have:
an = a + (n − 1) × d
95 = 10 + (n − 1) × 5
(n − 1) × 5 = 95 – 10 = 85
(n − 1) = 85/ 5
(n − 1) = 17
n = 17 + 1
n = 18
Example 2: Find the 20th term for the given AP:3, 5, 7, 9, ……
Sol: Given,
3, 5, 7, 9, ……
a = 3, d = 5 – 3 = 2, n = 20
an = a + (n − 1) × d
a20 = 3 + (20 − 1) × 2
a20 = 3 + 38
⇒a20 = 41
Sum of n terms of an A.P.
The sum of the first n terms of an A.P. is given by
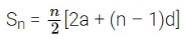 where [a = first term, d = common difference, n = term number
where [a = first term, d = common difference, n = term number
Example: Find the sum of the first 30 multiples of 4.
Sol: The first 30 multiples of 4 are: 4, 8, 12, ….., 120
Here, a = 4, n = 30, d = 4
We know,
S30 = n/2 [2a + (n − 1) × d]
S30 = 30/2[2 (4) + (30 − 1) × 4]
S30 = 15[8 + 116]
S30 = 1860
Note: If a, b, c are in A.P. then b =
and b is called the arithmetic mean of a and c.
|
127 videos|584 docs|79 tests
|
FAQs on Arithmetic Progressions Class 10 Notes Maths Chapter 5
| 1. What is a sequence in mathematics? |  |
| 2. What is an Arithmetic Progression (A.P.)? |  |
| 3. How do you find the nth term of an A.P.? |  |
| 4. What is the formula to calculate the sum of the first n terms of an A.P.? |  |
| 5. Can you give an example of an A.P. and calculate its sum? |  |















