Triangles Class 10 Notes Maths Chapter 6

Similar Figures

1. Two figures having the same shape but not necessary the same size are called similar figures.
2. All congruent figures are similar but all similar figures are not congruent.

For Example: 

(i) Any two line segments are similar since length are proportional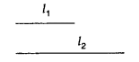

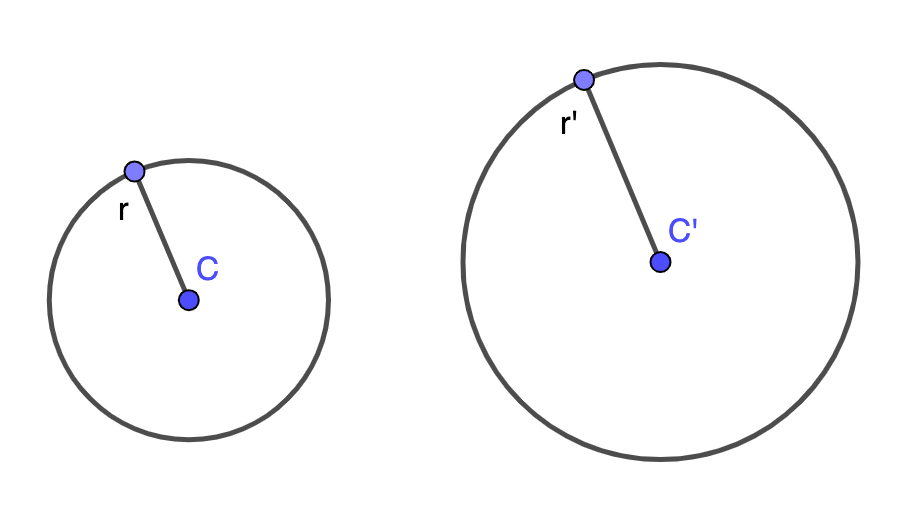
(ii) Any two circles are similar since radii are proportional

(iii) Any two squares are similar since corresponding angles are equal and lengths are proportional.

Note: Similar figures are congruent if there is one to one correspondence between the figures.

Similar Polygons

Two polygons are said to be similar to each other, if:

1. Their corresponding angles are equal, and
2. The lengths of their corresponding sides are proportional
   

For Example:

From above we deduce:

Any two triangles are similar, if their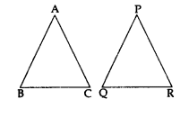

(i) Corresponding angles are equal

• ∠A = ∠P
• ∠B = ∠Q
• ∠C = ∠R

(ii) Corresponding sides are proportional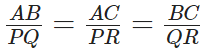

Thales Theorem or Basic Proportionality Theory

Theorem 1:  If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.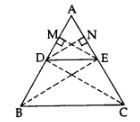

Proof of Thales Theorem

Given: In ∆ABC, DE || BC.

To prove: AD/DB = AE/EC

Const.: Draw EM ⊥ AD and DN ⊥ AE. Join B to E and C to D.

Proof: In ∆ADE and ∆BDE, 

 ……..(i) [Area of ∆ = 1/2 x base x corresponding altitude]

In ∆ADE and ∆CDE,

∵ DE || BC …[Given ]

∴ ar(∆BDE) = ar(∆CDE) 

…[∵ As on the same base and between the same parallel sides are equal in area]

From (i), (ii) and (iii),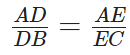

Criterion for Similarity of Triangles

Two triangles are similar if either of the following three criterion’s are satisfied:

• AAA similarity Criterion. If two triangles are equiangular, then they are similar.
• Corollary(AA similarity). If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.
• SSS Similarity Criterion. If the corresponding sides of two triangles are proportional, then they are similar.
• SAS Similarity Criterion. If in two triangles, one pair of corresponding sides are proportional and the included angles are equal, then the two triangles are similar.

Results in Similar Triangles based on Similarity Criterion:

• Ratio of corresponding sides = Ratio of corresponding perimeters
• Ratio of corresponding sides = Ratio of corresponding medians
• Ratio of corresponding sides = Ratio of corresponding altitudes
• Ratio of corresponding sides = Ratio of corresponding angle bisector segments.

Area of Similar Triangles

Theorem 2. The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Given: ∆ABC ~ ∆DEF 
To prove: 
Const.: Draw AM ⊥ BC and DN ⊥ EF. 
Proof: In ∆ABC and ∆DEF 

…(i) ……[Area of ∆ = 1/2 x base x corresponding altitude]
∵ ∆ABC ~ ∆DEF 
 …..(ii) …[Sides are proportional]
∠B = ∠E ……..[∵ ∆ABC ~ ∆DEF ]
∠M = ∠N …..[each 90° 
∴ ∆ABM ~ ∆DEN …………[AA similarity] 
 …..(iii) …[Sides are proportional]
From (ii) and (iii), we have: 
From (i) and (iv), we have: 
Similarly, we can prove that 

Results based on Area Theorem: 

• Ratio of areas of two similar triangles = Ratio of squares of corresponding altitudes
• Ratio of areas of two similar triangles = Ratio of squares of corresponding medians
• Ratio of areas of two similar triangles = Ratio of squares of corresponding angle bisector segments.

Note: If the areas of two similar triangles are equal, the triangles are congruent.

Pythagoras Theorem

Theorem 3: In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Proof of Pythagoras Theorem

Given: ∆ABC is a right triangle right-angled at B.

To prove: AB² + BC² = AC²

Const.: Draw BD ⊥ AC

Proof: In ∆s ABC and ADB, 

∠A = ∠A …[common]

∠ABC = ∠ADB …[each 90°]

∴ ∆ABC ~ ∆ADB …[AA Similarity]

 ………[sides are proportional] 

⇒ AB² = AC.AD 

Now in ∆ABC and ∆BDC

∠C = ∠C …..[common]

∠ABC = ∠BDC ….[each 90°]

∴ ∆ABC ~ ∆BDC …..[AA similarity] 

  ……..[sides are proportional] 

BC² = AC.DC …(ii)

On adding (i) and (ii), we get

AB² + BC² = ACAD + AC.DC

⇒ AB² + BC² = AC.(AD + DC)

AB² + BC² = AC.AC

∴ AB² + BC² = AC² 

Converse of Pythagoras Theorem

Theorem 4: In a triangle, if square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.

Proof of

Converse of Pythagoras Theorem

Given: In ∆ABC, AB² + BC² = AC²

To prove: ∠ABC = 90°

Const.: Draw a right angled ∆DEF in which DE = AB and EF = BC

Proof: In ∆ABC,

AB² + BC² = AC² …(i) [given]

In rt. ∆DEF

DE² + EF² = DF² …[by pythagoras theorem]

AB² + BC² = DF² …..(ii) …[DE = AB, EF = BC]

From (i) and (ii), we get

AC² = DF²

⇒ AC = DF

Now, DE = AB …[by cont]

EF = BC …[by cont]

DF = AC …….[proved above]

∴ ∆DEF ≅ ∆ABC ……[SSS congruence]

∴ ∠DEF = ∠ABC …..[CPCT]

∠DEF = 90° …[by cont]

∴ ∠ABC = 90° 

Results based on Pythagoras’ Theorem:
(i) Result on obtuse Triangles.
If ∆ABC is an obtuse angled triangle, obtuse angled at B,
If AD ⊥ CB, then
AC² = AB² + BC² + 2 BC.BD 

(ii) Result on Acute Triangles.
If ∆ABC is an acute angled triangle, acute angled at B, and AD ⊥ BC, then
AC² = AB² + BC² – 2 BD.BC.